按照某种遍历方式对二叉树进行遍历,可以把二叉树中所有结点排序为一个线性序列。在该序列中,除第一个结点外每个结点有且仅有一个直接前驱结点;除最后一个结点外每一个结点有且仅有一个直接后继结点。这些指向直接前驱结点和指向直接后续结点的指针被称为线索(Thread),加了线索的二叉树称为线索二叉树。
n个结点的二叉链表中含有n+1个空指针域。利用二叉链表中的空指针域,存放指向结点在某种遍历次序下的前趋和后继结点的指针(这种附加的指针称为"线索")。
这种加上了线索的二叉链表称为线索链表,相应的二叉树称为线索二叉树(Threaded BinaryTree)。根据线索性质的不同,线索二叉树可分为前序线索二叉树、中序线索二叉树和后序线索二叉树三种。
注意:
线索链表解决了二叉链表找左、右孩子困难的问题,出现了无法直接找到该结点在某种遍历序列中的前趋和后继结点的问题。
线索二叉树结构
二叉树的遍历本质上是将一个复杂的非线性结构转换为线性结构,使每个结点都有了唯一前驱和后继(第一个结点无前驱,最后一个结点无后继)。对于二叉树的一个结点,查找其左右子女是方便的,其前驱后继只有在遍历中得到。为了容易找到前驱和后继,有两种方法。一是在结点结构中增加向前和向后的指针fwd和bkd,这种方法增加了存储开销,不可取;二是利用二叉树的空链指针。现将二叉树的结点结构重新定义如下:
lchild ltag data rtag rchild
其中:ltag=0 时lchild指向左子女;
ltag=1 时lchild指向前驱;
rtag=0 时rchild指向右子女;
rtag=1 时rchild指向后继;
建立线索二叉树,或者说对二叉树线索化,实质上就是遍历一颗二叉树。在遍历过程中,访问结点的操作是检查当前的左,右指针域是否为空,将它们改为指向前驱结点或后续结点的线索。为实现这一过程,设指针pre始终指向刚刚访问的结点,即若指针p指向当前结点,则pre指向它的前驱,以便设线索。
另外,在对一颗二叉树加线索时,必须首先申请一个头结点,建立头结点与二叉树的根结点的指向关系,对二叉树线索化后,还需建立最后一个结点与头结点之间的线索。‘’
打开IDE
我们创建一个工程如下
创建一个二叉树基本类
#if !defined(AFX_TBSTREE_H__734128DD_1E78_4C94_B09C_BB135D79A339__INCLUDED_)
#define AFX_TBSTREE_H__734128DD_1E78_4C94_B09C_BB135D79A339__INCLUDED_
#if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000
//线索二叉树结点类型存储结构体TBSTree.h
template<class T> class TBSTree;
template<class T> class ITBSTree;
template<class T> struct THNode
{public:
int lflag,rflag;//标志域
THNode<T> *left;//第一个孩子结点指针域
THNode<T> *right;//下一个兄弟结点指针域
T data;//数据域
friend class TBSTree<T>;//线索二叉树类为友元
friend class ITBSTree<T>;
//构造函数
THNode():left(NULL),right(NULL),lflag(0),rflag(0){ }
THNode(int la,int ra,T value,THNode<T> *fc=NULL,
THNode<T> *ns=NULL):data(value),left(fc),
right(ns){lflag=la;rflag=ra;}
//访问指针域的成员函数
THNode<T>* &FirstChild()
{return left;}
THNode<T>* &NextSibling()
{return right;}
};
//线索二叉树类
template<class T> class TBSTree
{protected:
THNode<T> *root;//根结点指针
THNode<T> *curr;//当前结点指针
int nextC;
int priorC;
public:
//构造函数与析构函数
TBSTree(){root=curr=NULL;}
TBSTree(THNode<T> *&tree)
{root=tree;
curr=root;
if(tree==NULL)
{nextC=1;priorC=1;}
else {nextC=0;priorC=0;}
}
//纯虚函数
virtual THNode<T> *First()=0;
virtual void Next()=0;
virtual void Last()=0;
virtual void Prior()=0;
int EndOfNext()
{return nextC;}
int EndOfPrior()
{return priorC;}
//数据检索与修改成员函数
T &Data();
};
//线索二叉树类的实现
template<class T>
T &TBSTree<T>::Data()
{if(root==NULL)
{cout<<"二叉树空!\n";exit(1);}
return curr->data;
}
//由结点构造线索二叉树的类外一般函数
template<class T>
THNode<T> *GetTreeNode(T item,THNode<T> *le=NULL,
THNode<T> *ri=NULL,int lf=0,int rf=0)
{THNode<T> *p=new THNode<T>;
p->data=item;p->left=le;p->right=ri;
p->lflag=lf;p->rflag=rf;
if(p==NULL)
{cerr<<"内存分配失败!\n";exit(1);}
return p;
}
//创建特定线索二叉树的类外一般函数
template<class T>
THNode<T> *MakeCharT(THNode<T> *&root,int num)
{THNode<T> *b,*c,*d,*e,*f,*g,*null=NULL;
if(num==1)
root=GetTreeNode('X',null);
if(num==2)
{e=GetTreeNode('R');
f=GetTreeNode('W');
d=GetTreeNode('P',e,f);
g=GetTreeNode('Q');
b=GetTreeNode('N',d,g);
c=GetTreeNode('O');
root=GetTreeNode('M',b,c);
}
if(num==3)
{g=GetTreeNode('G');
d=GetTreeNode('D',null,g);
b=GetTreeNode('B',d);
e=GetTreeNode('E');
f=GetTreeNode('F');
c=GetTreeNode('C',e,f);
root=GetTreeNode('A',b,c);
}
return root;
}
#endif // !defined(AFX_TBSTREE_H__734128DD_1E78_4C94_B09C_BB135D79A339__INCLUDED_)
创建一个二叉线索树派生二叉树
#if !defined(AFX_ITBSTREE_H__8F1F1BC6_2A9C_4B63_9293_7FE5AD325AA7__INCLUDED_)
#define AFX_ITBSTREE_H__8F1F1BC6_2A9C_4B63_9293_7FE5AD325AA7__INCLUDED_
#if _MSC_VER > 1000
#pragma once
#endif // _MSC_VER > 1000
#include "TBSTree.h"
//派生类ITBSTree.h
template<class T>
class ITBSTree:public TBSTree<T>
{private:
//中序线索化二叉树
void InThread(THNode<T> *&root,THNode<T> *&pre);
public:
//构造函数
ITBSTree(THNode<T> *&tree):TBSTree<T>(tree) {}
//中序线索化二叉树
void CreatInThread();
//定位到中序下的第一个结点
virtual THNode<T> *First();
//将当前指针移到中序下的后继结点
virtual void Next();
//定位到中序下的最后一个结点
virtual void Last();
//将当前指针移到中序下的前驱结点
virtual void Prior();
//插入结点
void InsertR(THNode<T> *&s,THNode<T> *&r);
};
template<class T>
void ITBSTree<T>::InThread(THNode<T> *&root,THNode<T> *&pre)
{if(root!=NULL)
{InThread(root->left,pre);//中序线索化左子树二叉树
if(root->left==NULL)//当前结点左指针为空指针时
{root->lflag=1; //建立左线索指针
root->left=pre;//建立左线索标志
}
if(pre->right==NULL)//前驱结点右指针为空指针时
{pre->rflag=1; //建立右线索标志
pre->right=root;//建立右线索指针
}
pre=root;//前驱结点右指针等于当前结点指针
InThread(root->right,pre);}//中序线索化右子树二叉树
}
template<class T>
void ITBSTree<T>::CreatInThread()
{THNode<T> *t=root;//保存原根结点指针
root=new THNode<T>;//建立头结点
root->lflag=0;
root->rflag=1;
if(t==NULL)//当为空树时
{root->left=root;
root->right=root;
}
else //当为非空树时
{curr=root->left=t;//置头结点的左指针
root->lflag=0; //置头结点的左标志
THNode<T> *pre=root;//定义临时指针
InThread(curr,pre);//中序线索化二叉树
pre->right=root;//置最后一个结点的右线索
pre->rflag=1; //置最后一个结点的右标志
root->right=pre;//置头结点的右线索
root->rflag=1;//置头结点的右标志
}
}
template<class T>
THNode<T> *ITBSTree<T>::First()
{curr=root;//从根结点开始
while(curr->lflag==0)
curr=curr->left;
if(curr==root) nextC=1;//当二叉树为空时
else nextC=0;//当二叉树为非空时
return curr;
}
template<class T>
void ITBSTree<T>::Next()
{if(nextC==1)
{cerr<<"已到二叉树尾!\n";exit(1);}
THNode<T> *p=curr->right;//将当前指针移到中序下的后继结点
if(curr->rflag==0)
while(p->lflag==0) p=p->left;
curr=p;
if(curr==root) nextC=1;
}
template<class T>
void ITBSTree<T>::Last()
{curr=root->right;//使curr定位到中序下的最后一个结点
if(curr==root) priorC=1;
else priorC=0;
}
template<class T>
void ITBSTree<T>::Prior()
{if(priorC==1)
{cerr<<"已到二叉树头!\n";exit(1);}
THNode<T> *p=curr->left;
if(curr->lflag==0)
while(p->rflag==0) p=p->right;
curr=p;
if(curr==root) priorC=1;
}
template<class T>
void ITBSTree<T>::InsertR(THNode<T> *&s,THNode<T> *&r)
{//将r当做s的右子女插入
r->right=s->right;//s的右子女指针或后继线索传给r
r->rflag=s->rflag;//传送标志
r->left=s;r->lflag=1;//r的left成为指向s的前驱线索
s->right=r;s->rflag=0;//r成为s的右子女
if(r->rflag==0)//s原来有右子女
{curr=r->right;
THNode<T> *temp=First();//在s原来的右子树中找中序下第一个结点
temp->left=r;//建立指向r的前驱线索
}
}
#endif // !defined(AFX_ITBSTREE_H__8F1F1BC6_2A9C_4B63_9293_7FE5AD325AA7__INCLUDED_)
代码调用如下,
void main()
{cout<<"运行结果:\n";
THNode<char> *q,*p,*r;
q=MakeCharT(q,3);
ITBSTree<char> t(q);
t.CreatInThread();
cout<<"线索二叉树的中序正向遍历序列为:\n";
for(t.First();!t.EndOfNext();t.Next())
cout<<t.Data()<<" ";
cout<<"\n线索二叉树的中序反向遍历序列为:\n";
for(t.Last();!t.EndOfPrior();t.Prior())
cout<<t.Data()<<" ";
p=MakeCharT(p,2);
ITBSTree<char> d(p);
d.CreatInThread();
cout<<"\n线索二叉树的中序正向遍历序列为:\n";
for(d.First();!d.EndOfNext();d.Next())
cout<<d.Data()<<" ";
cout<<"\n线索二叉树的中序反向遍历序列为:\n";
for(d.Last();!d.EndOfPrior();d.Prior())
cout<<d.Data()<<" ";
r=MakeCharT(r,1);
ITBSTree<char> h(r);
h.CreatInThread();
cout<<"\n线索二叉树的中序正向遍历序列为:\n";
for(h.First();!h.EndOfNext();h.Next())
cout<<h.Data()<<" ";
d.InsertR(p,r);
cout<<"\n插入结点后线索二叉树的中序正向遍历序列为:\n";
for(d.First();!d.EndOfNext();d.Next())
cout<<d.Data()<<" ";
cin.get();
}效果如下
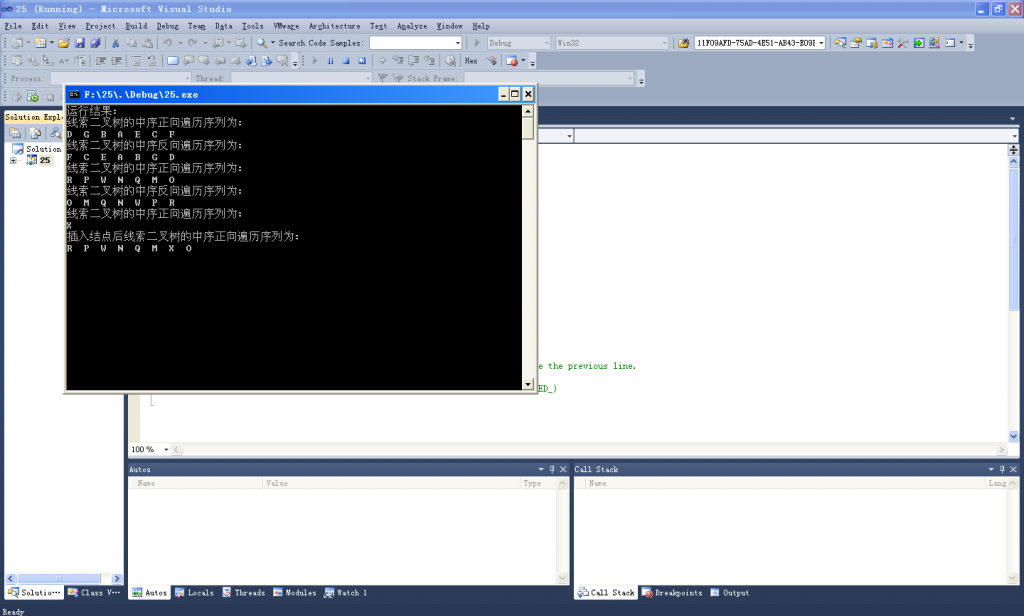
代码下载如下
http://download.csdn.net/detail/yincheng01/4789691