2020.3.24 B组总结

T1:折纸

题目大意：

(Onise)喜欢画画. 他有一张 (width * height)的纸.他在纸上的操作步骤如下:

1. 从直线 (x = xfold) 对折(是把左边的纸折到右边上面)；

2. 把纸竖直对折成(cnt+1)等份，就是把最上面的折到下面,共操作(cnt)次；

3. 现在(Onise),画一个实心矩行,左下角的坐标是((x1, y1)),右上角坐标是 ((x2, y2))。注意: ((x1, y1)) 、((x2, y2))是把纸折完之后的坐标，((0, 0))是左下角坐标, (Onise)画的那些格子的墨水都会渗到它对应的下层的那些格子；

4. 再次展开纸。

给你纸的(width)和(height)、(xfold)、(cnt)、(x1)、(y1)、(x2)、(y2)，请问画完之后，还有多少个格子是没有被渗到颜色的。

正解：数学

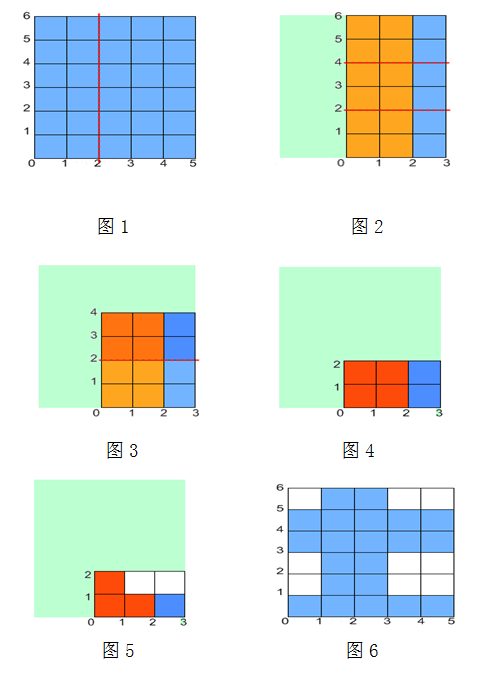
如图(5)是折后的图形。

白色部分是沾墨水的部分。
由题可知白色部分必定是一个矩形。
所以我们可以先求出墨水沾到的大小。
再用整个纸的大小减去沾墨水的大小就是答案

考虑竖折，必定是(cnt+1)块叠在一起，所以竖折对答案的贡献是((cnt+1)*白色部分的块数)

考虑横折，

所以，只用考虑范围内的白块，贡献就是(2*(cnt+1)*范围内的白块个数)

#include<cstdio>
#include<iostream>
#define ll long long
using namespace std;

int main()
{
	int t;
	scanf("%d",&t);
	while (t--)
	{
		ll w,h,xf,cnt,x1,x2,y1,y2;
		scanf("%lld%lld%lld%lld%lld%lld%lld%lld",&w,&h,&xf,&cnt,&x1,&y1,&x2,&y2);
		xf=min(xf,w-xf);
		ll res=(x2-x1)*(y2-y1)*(cnt+1);
		if (x2>=xf)
		{
			if (x1<xf) 
				res+=(xf-x1)*(y2-y1)*(cnt+1);
		}
		else res=res*2;
		ll ans=w*h-res;
		printf("%lld
",ans);
	}
}

T2:等待·····

T3:游戏

题目大意:

农夫FJ和奶牛Bessie玩游戏，游戏由一个黑板和N张卡片组成。游戏初始时，黑板写的数字是0。每张卡片都写有一个[0,511]的整数。FJ和Bessie轮流操作，FJ先操作。操作者每次从当前的卡片中选取一张卡片出来(被选出来的卡片不会被再次利用)，假设选出来的卡片写的数是X，并假设当前黑板写的数是Y，那么本轮操作后黑板的数变成Y|X，其中|是位操作的或。如果某个操作者没有卡片可取了（卡片已经取完），那么该操作者输。如果某操作者进行某次操作后，黑板上的数变成了511，那么该操作者输。假设FJ和Bessie都采取最优策略，那么最后胜利者是谁？

正解:记忆化搜索（或(DP)）

(511) 其实就是一个二进制数：(111111111)，因此算法选择为状态 (DP)。
首先可用一个二进制数 (S) 的位表示有哪些位已经是 (1) 或 (0)。(DP) 到第 (i) 轮时，还要记录哪
些卡片没有取---集合 (SC)。关键是 (SC) 十庞大，不能直接记录。(SC) 中的数分两类：一类是不影
响状态 (S) 的数，只要记录个数即可；另一类是影响状态 (S) 的数，不用记录，可用通过 (S) 看哪
些数对它有影响，需要时重新计算。
只要记录 (F[i , S ])即可。可记忆化搜索。

#include<cstdio>
#include<cstring>
using namespace std;
int a[1000],f[1000][1000],n,t;

int dfs(int x,int s)
{
	int k=0;
	if (f[x][s]) return f[x][s];
	if (s==511) return f[x][s]=1;
	if (x==n) return f[x][s]=-1;
	for (int i=1;i<=n;i++)
		if ((s|a[i])!=s)
		{
			if (dfs(x+1,a[i]|s)==-1) return f[x][s]=1;
		}else k++;
	if (k>x)
		if ((k-x)%2==1) return f[x][s]=-dfs(k,s);
		else return f[x][s]=dfs(k,s);
	return f[x][s]=-1;
		
}
int main()
{
	scanf("%d",&t);
	while (t--)
	{
		memset(f,0,sizeof(f));
		scanf("%d",&n);
		for (int i=1;i<=n;i++) 
			scanf("%d",&a[i]);
		printf("%d
",dfs(0,0));
	}
}