第6章 树型结构

第6章 树型结构

目录

• 第6章 树型结构
• 一、树的基本概念
• 二、树类的定义
• 三、树的存储结构 （大概率不考）
  • 3.1 双亲表示法
    • 3.1.1 树的存储结构（双亲表示法）
  • 3.2 孩子表示法
  • 3.3 孩子兄弟表示法
• 四、树的遍历
• 五、树的线性表示（大纲未规定）
  • 5.1 树的括号表示
  • 5.2 树的层号表示
• 六、算法设计题
• 七、错题集

数据结构与算法_师大完整教程目录（更有python、go、pytorch、tensorflow、爬虫、人工智能教学等着你）：https://www.cnblogs.com/nickchen121/p/13768298.html

一、树的基本概念

1. 树：由 (n(n>=0)) 个结点构成的有限集合
2. 根：有且仅有一个特定的结点
3. 结点的度：结点拥有的子女数
4. 树的度：所有结点度的最大值
5. 度为 (0) 的结点：终端结点（叶子结点）
6. 度不为 (0) 的结点：非终端结点（分支结点）
7. 树枝：连接两个结点的线段
8. 结点的层次：根结点为第 (1) 层，根的子女结点为第 (2) 层
9. 树的高度：树中结点最大层次树
10. 有序树：任意结点的子树看成是从左到右有次序，不能随意交换，否则为无序树
11. 森林：(m(m>=0)) 棵互不相交的树构成的集合（在森林的每棵树之上加一个共同的根，森林则成了一棵树）

二、树类的定义

1. 略

三、树的存储结构 （大概率不考）

1. 树的三种常用存储结构：双亲表示法、孩子表示法、孩子兄弟表示法

3.1 双亲表示法

1. 树的结点包含两个信息：结点的值 (data) 和体现结点之间相互关系的属性——该结点的双亲 (parent)

3.1.1 树的存储结构（双亲表示法）

#define MAXSIZE 100 // 树中结点个数的最大值
typedef char datatype;   // 结点值的类型
// 结点的类型
typedef struct node {
    datatype data;
    int parent; // 结点双亲的下标
} node;
// 树的类型
typedef struct tree {
    node treelist[MAXSIZE]; // 存放结点的数组
    int length, root; // 树中实际所含结点的个数及根节点的位置
} tree;

3.2 孩子表示法

1. 略

3.3 孩子兄弟表示法

1. 略

四、树的遍历

1. 前序遍历：首先访问根结点，再从左到右依次按前序遍历的方式访问根结点的每一棵子树

2. 后序遍历：首先按后序遍历的方式访问根结点的每一棵子树，然后再访问根结点

3. 层序遍历：首先访问第一层上的根结点，然后从左到右依次访问第二层上的所有结点，……，最后访问树中最低一层的所有结点。

4. 图树的遍历：

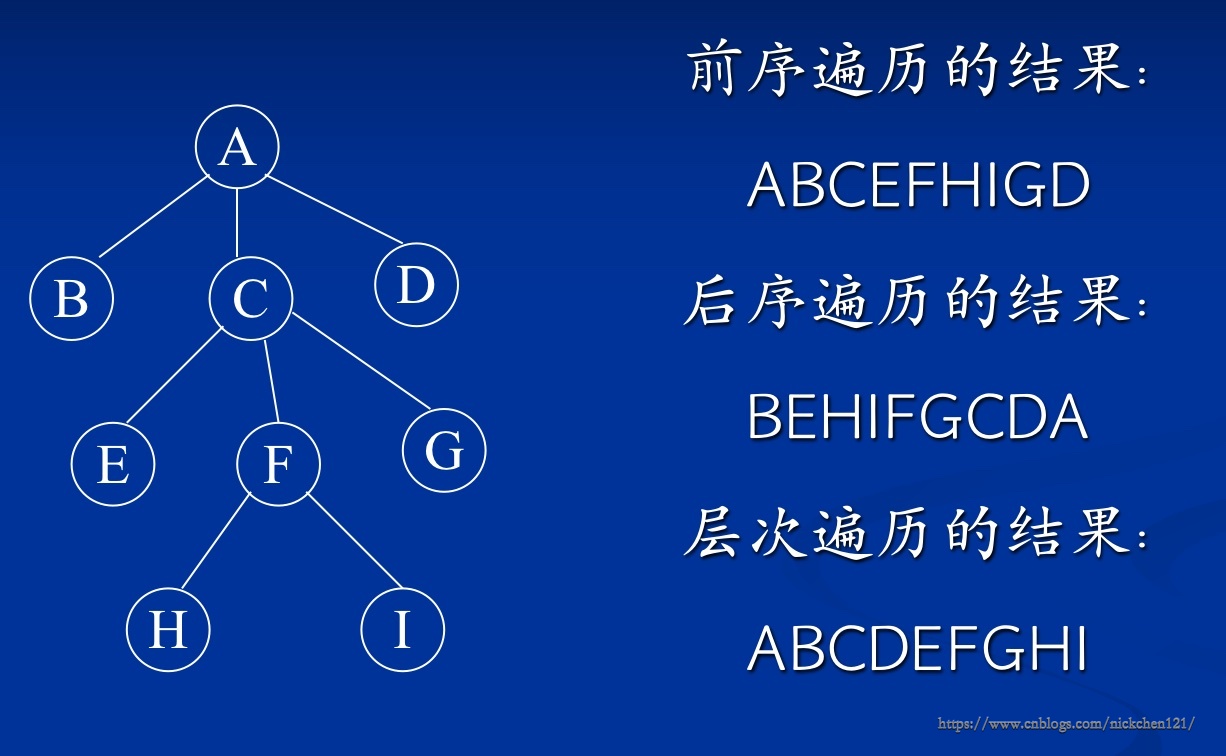
5. 树的遍历常用操作：

   1. 树的前续遍历的递归算法
   2. 树的后序遍历的递归算法
   3. 按前序遍历顺序建立一颗 (3) 度树
   4. 树的层次遍历算法

五、树的线性表示（大纲未规定）

1. 注：仅凭借树的某种遍历序列有时无法唯一地确定一棵树，但只要在遍历序列的基础上加上一些附加信息，即可唯一地确定一棵树

5.1 树的括号表示

1. 常用操作：

   1. 树的括号表示到树的孩子表示的转换算法

2. 图树的括号表示：

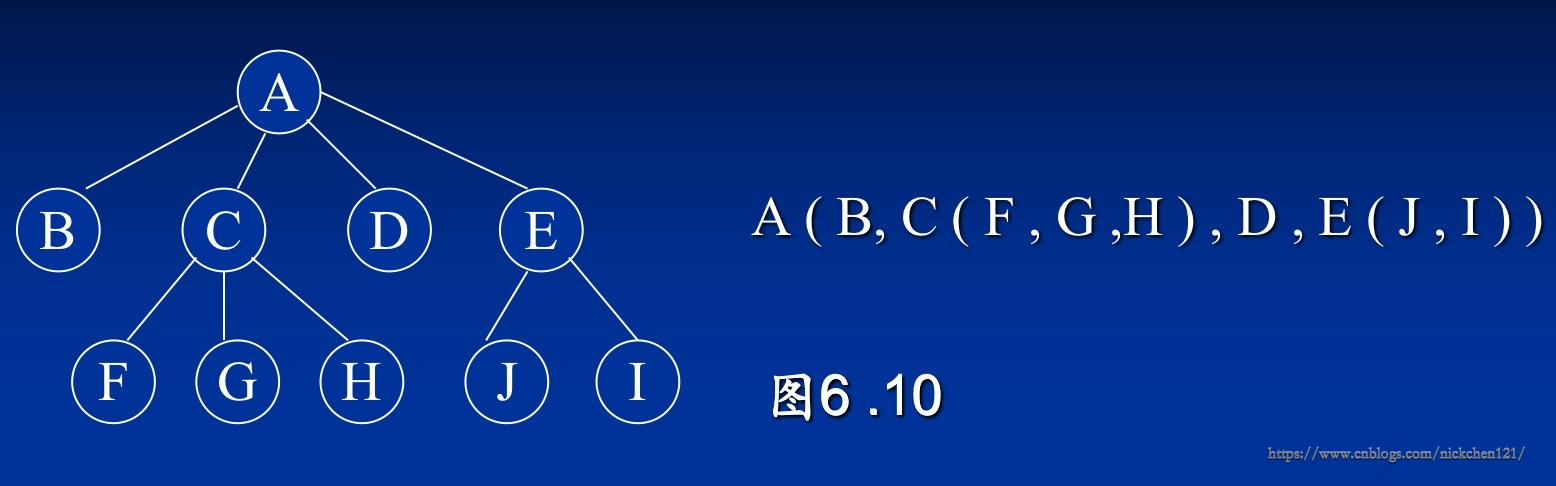
5.2 树的层号表示

1. 常用操作：

   1. 树的层号表示到树的扩充孩子表示的转换算法

2. 图树的层号表示：

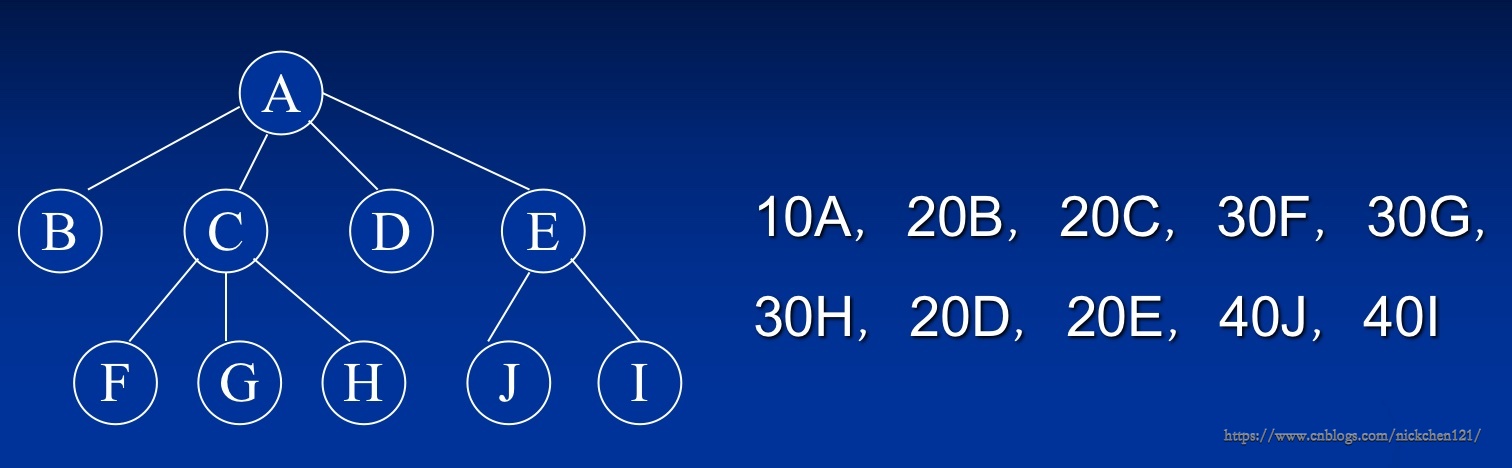
六、算法设计题

1. 略

七、错题集

1. 树最适合用来表示具有有序性和层次性的数据

2. 在选择存储结构时，既要考虑数据值本身的存储，还需要考虑数据间关系的存储

3. （真题）对于一颗具有 (n) 个结点的树，该树中所有结点的度数之和为 (n-1)

4. 已知一棵度为 (m) 的树中有 (n_1) 个度为 (1) 的结点， (n_2) 个度为 (2) 的结点，……，(n_m) 个度为
   (m) 的结点，问该树中有多少个叶子结点？

   1. 树中结点总数 (n=n_0+n_1+n_2+…+n_m)
   2. 树中结点的度数之和为 (n-1)，且有：(n-1=n_1+2*n_2+3*n_3+cdots+m*n_m) （用上题 (3) 的定理）
   3. 所以叶子结点个数为：(n_0=1+n_2+2*n_3+cdots+(m-1)*n_m)