树是一种一对多的数据结构,之前的数组,栈这些都是一对一的数据结构。
树是n个结点的有限集。n=0称空树。在任意一棵非空树中:有且仅有一个根(root)结点;n>1时,其余结点可分为m个互不相交的的有限集,其中每个集合又是一棵树,称为根的子树。
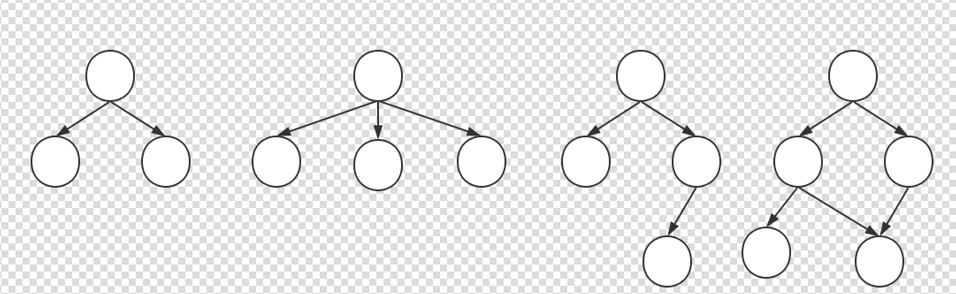
前面三个都是树,最后一个不是树,因为最后一个的数据相交了。
树结构中的术语:
以下图为例
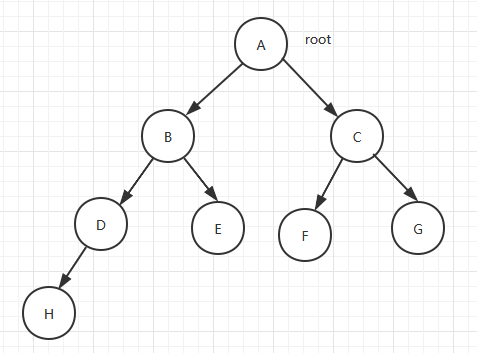
结点:树上面的元素
父子关系:结点之间相连的边
子树:当结点大于1时,其余的结点分为的互不相交的集合称为子树.
度:一个结点拥有的子树数量称为结点的度(A是root结点度是2,B的度是2,D的度是1)
叶子:度为0的结点(H,E,F,G)
孩子:结点的子树的根称为孩子结点
双亲:和孩子结点对应,一个孩子只有一个双亲(A是B的双亲)
兄弟:同一个双亲结点(B,C)
森林:由多个互不相交的树构成深林
结点高度:结点到叶子结点的最长路径(A的高度3,B的高度2,H的高度0)
结点深度:根结点到该结点的边个数(B结点深度1,H结点深度3)
结点的层数:结点的深度加1
树的高度:根结点的高度
树的深度:树的高度+1
树的表示方法:
双亲表示法:由孩子来记住双亲的位置
public class TreeNode<T> { private T data; private TreeNode<T> parent; }
孩子表示法:由双亲来记住所有孩子的位置
public class TreeNode<T> { private T data; private TreeNode<T> leftChild; private TreeNode<T> rightChild; }
二叉树:
二叉树是由一个根结点和两棵互不相交的,分别称为根结点的左子树和右子树的二叉树构成。二叉树的每个最多有两棵子树。也就说二叉树每个结点的度是不会超过2的。
比如上面的ABCDEFGH就是一棵二叉树。二叉树非常适合用于每个阶段都存在两种结果的情形的建模。比如开关,01,真假,上下,对错,正反,选不选(前面动态规划分析的那个图)
特殊的二叉树:
斜树:所有结点都只有左子树的叫做左斜树,所有结点只有右子树的叫做右斜树
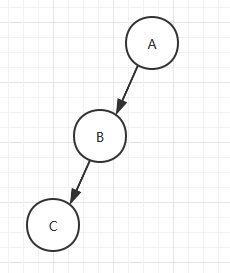
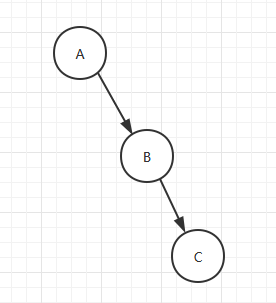
满二叉树:所有结点都存在左右子树,并且所有的叶子都在同一层

完全二叉树:每一层的叶子结点都是相邻的没有间隔,满二叉树也是一种特殊的完全二叉树

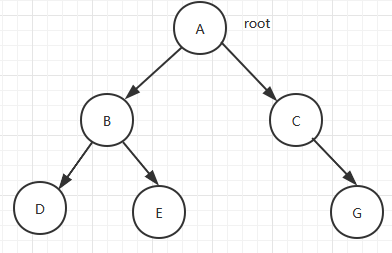
后面的就不是完全二叉树,因为E和G不相邻了。完全二叉树可以基于数组存储。前面也有说到数组可以基于下标查询,而且它在内存中是连续,CPU有会预读相邻的区域的。
完全二叉树怎么用数组存储呢?
双亲索引为i,那么它的左孩子就是2i,右孩子就是2i+1
比如上面这个完全二叉树转换成数组表示:

F是C的左孩子:C在3,F在6,刚好是2n
非完全二叉树也用数组存储的话,会导致很多内存浪费,分配了却没有使用。
二叉树的遍历:
遍历如下这个二叉树:

先来用代码来构建这棵二叉树:
/** * 构造二叉树 * @param dataList * @param <T> * @return */ public static <T> TreeNode<T> createBinaryTree(LinkedList<T> dataList) { TreeNode<T> node = null; if (dataList == null || dataList.isEmpty()) { return null; } T data = dataList.removeFirst(); if (data != null) { node = new TreeNode(data); node.setLeftChild((createBinaryTree(dataList))); node.setRightChild((createBinaryTree(dataList))); } return node; }
调用方式:
LinkedList<String> inputList = new LinkedList<>( Arrays.asList(new String[]{"A","B","D","H",null,null,null,"E",null,null,"C","F",null,null,"G"})); TreeNode<String> treeNode = createBinaryTree(inputList);
调用里面传的部分null值,是因为有些结点没有孩子结点,比如H,根据写的构造树方法(createBinaryTree)的逻辑传入合适的null值。
遍历有关键点:不管哪种遍历,按照其顺序遇根输出
前序遍历:根 左 右
按照根左右的顺序,遇根输出,再去找左
上面这棵树的结果应该是ABDHECFG
因为遍历的时候 对于每个节点的操作都是一样的,所以我们首先想到的就是使用递归
/** * 前序遍历 根 左子树 右子树 * @param node */ public static<T> void preOrderTraversal(TreeNode<T> node) { if(node == null){ return; } //遇根先输出,再去找左右 System.out.print(node.getData()); preOrderTraversal(node.getLeftChild()); preOrderTraversal(node.getRightChild()); }
也可以利用栈的特性来实现递归回溯的功能
/** * 利用栈前序遍历二叉树 * @param root */ public static <T> void preOrderTraversalByStack(TreeNode<T> root) { Stack<TreeNode<T>> stack = new Stack<>(); TreeNode<T> node = root; while(node != null || !stack.isEmpty()) { //节点不为空,遍历节点,并入栈用于回溯 while(node != null) { System.out.print(node.getData()); stack.push(node); node = node.getLeftChild(); } //没有左节点,弹出该栈顶节点(回溯),访问右节点 if(!stack.isEmpty()) { node = stack.pop(); node = node.getRightChild(); } } }
中序遍历:左 根 右
HDBEAFCG
/** * 二叉树中序遍历 左子树 根 右子树 * @param node 二叉树节点 */ public static<T> void inOrderTraversal(TreeNode<T> node){ if(node == null){ return; } //先找左再输出根,再去找右 inOrderTraversal(node.getLeftChild()); System.out.print(node.getData()); inOrderTraversal(node.getRightChild()); }
后序遍历:左 右 根
HDEBFGCA
/** * 二叉树后序遍历 左子树 右子树 根 * @param node 二叉树节点 */ public static<T> void postOrderTraversal(TreeNode<T> node){ if(node == null){ return; } //先找左右,最后输出根 postOrderTraversal(node.getLeftChild()); postOrderTraversal(node.getRightChild()); System.out.print(node.getData()); }
层次遍历:按层来遍历
ABCDEFGH
层次遍历的时候,利用队列的特性,将所有的孩子依次入队进行操作。
public static <T> void levelOrder(TreeNode<T> root) { if (root == null) { return; } Queue<TreeNode> queue = new LinkedList<>(); queue.offer(root); //入队 while (!queue.isEmpty()) { TreeNode<T> node = queue.poll(); //取出 if (node != null) { System.out.print(node.getData()); queue.offer(node.getLeftChild()); //左孩子入队 queue.offer(node.getRightChild()); //右孩子入队 } } }