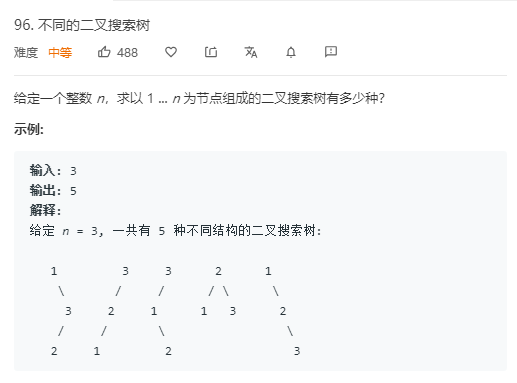
首先,我们假定求长度为 n 的数列可组成的二叉搜索树的数量为 G(n)。
想办法将 G(n) 用其子问题表示,如果我们以第 i 个元素为根,则其左子树的数量为 G(i-1),右子树的数量为 G(n-i) 。那么以第 i 个元素为根的二叉搜索树的数量为 G(i-1) 与 G(n-i) 两个集合的笛卡尔积:G(i-1)*G(n-i)。
想要覆盖全部解空间,我们必须将以每个元素为根的情况都计算出来,并求它们的和,那么状态转移方程即为:
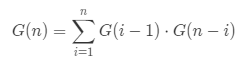
边界条件 G(0)=0 ;G(1)=1 ; 但是 G(0) 我们需要做特殊处理,对于我们的计算情景来说,如果一侧的二叉树种类为 0 ,那么总的种类应该是另一侧的种类,也就是说 G(0) 应当为 1。
同时 n-i 需大于等于 0 ,也就是 n 需要大于等于 1。
所以,计算 G(n) 依赖 G(0)、G(1) ... G(n-1) ,且 n >=1 。对该方程进行实现:
public int numTrees(int n) { if (n == 0) { return 0; } int[] g = new int[n + 1]; g[0] = 1; g[1] = 1; for (int i = 2; i <= n; i++) { for (int j = 1; j <= i; j++) { g[i] += g[j - 1] * g[i - j]; } } return g[n]; }
上面描述的 G(n) 函数被称为卡特兰数:

通过卡特兰数公式进行计算,可以将时间复杂度降低到 O(N):
public int numTrees(int n) { long C = 1; for (int i = 0; i < n; ++i) { C = C * 2 * (2 * i + 1) / (i + 2); } return (int) C; }
将问题分解为子问题,用子问题的解表示原问题的解。也就是问题表示问题,用函数表示函数,可以帮助我们直接找到解决问题所需要的上层逻辑,也就是问题间的逻辑关系。从而屏蔽掉很多不需要的底层逻辑细节,得到最简洁干净的表示方式。