随机变量:值并不固定
(1)离散型随机变量:抛硬币出现正反面的次数以及每周下雨的天数
(2)连续型随机变量:汽车每小时行驶的速度和银行排队的时间
总结:需要求和得出的就是离散型,需要积分计算得出的就是连续型
1. 离散性
例1:抛硬币
1 import random 2 import pandas as pd 3 import numpy as np 4 import matplotlib.pyplot as plt 5 6 def flip_coin(times): 7 data_array = np.empty(times) # 生成一个10行的矩阵,存放data [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 8 weights_array = np.empty(times) # 生成一个10行的矩阵,存放weight [0, 0, 0, 0, 0, 0, 0, 0, 0, 0] 9 weights_array.fill(1 / times) # [0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1] 10 11 for i in range(0, times): # 抛times次的硬币 12 data_array[i] = random.randint(0, 1) # 假设0表示正面,1表示反面 [0., 1., 1., 0., 0., 0., 0., 1., 0., 1.] 13 14 data_frame = pd.DataFrame(data_array) # 将矩阵数据进行格式化 15 data_frame.plot(kind='hist', legend=False) #获取正反面统计次数的直方图 16 data_frame.plot(kind='hist', legend=False, weights=weights_array).set_ylabel("Probability") # 获取正反面统计概率的直方图 17 plt.show() 18 19 flip_coin(10)
抛10次的结果
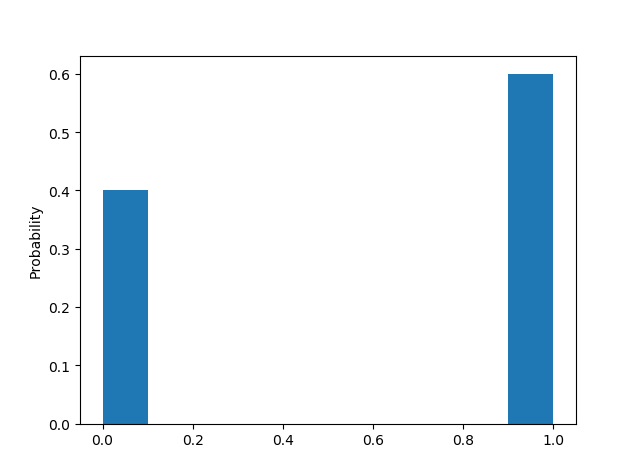
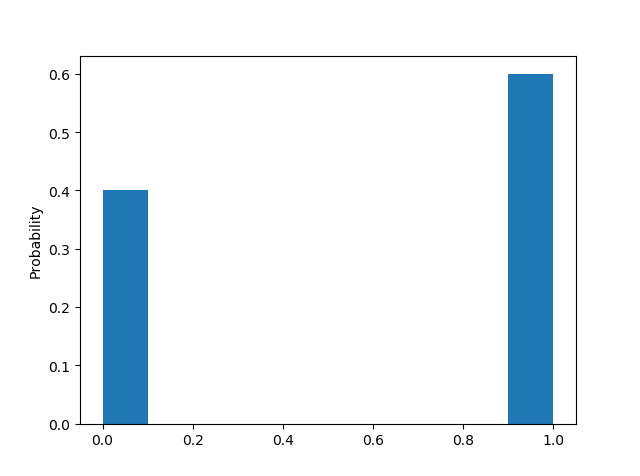
随着抛硬币次数越来越多,正面反面出现次数趋近于一致
也就是说,统计的采样次数越多,越趋近于我们理论上的情况。因此,从这个统计实验我们可以看出,概率分布描述的其实就是随机变量的概率规律。
2. 连续型
抛硬币正面次数、每周下雨天数这种离散型随机变量,对应的概率分布是很好理解的,但是对于连续型的随机变量,如何理解它们的概率分布呢?
将连续数据离散化
例如汽车速度仪表盘:现实生活中我们通过汽车的仪表盘所读取速度,都是整数值,例如每小时 60 公里。也许比较高档的车会显示数字化的速度,带有小数位,但实际上汽车最精确的速度是一个无限位数的小数,是从 0 到最高公里数的一个任意数值。所以仪表盘所显示的数字,是将实际速度离散化处理之后的数字。除了仪表盘上的速度,汽车行驶在时间维度上也是连续的。类似地,我们还需要对时间进行离散化,比如每分钟查看仪表盘一次并读取速度值。
例二:模拟汽车仪表盘,记录行车速度
假设:仪表盘最小刻度是 5,也就是说,它只能显示 55、60、65 这种公里数。然后每 1 分钟采样一次(读一次仪表盘),那么 1 小时内我们将生成 60 个数据。示例代码如下:
1 import random 2 import pandas as pd 3 import numpy as np 4 import matplotlib.pyplot as plt 5 6 7 def check_speed(time_gap, speed_gap, total_time, min_speed, max_speed): 8 9 times = int(total_time / time_gap) # 获取读取仪表盘的次数 10 11 data_array = np.empty(times) # [0, 0, 0, ...] 60个 12 weights_array = np.empty(times) # [0, 0, 0, ...] 60个 13 weights_array.fill(1 / times) # [0.01666667, 0.01666667, 0.01666667,.....] 60个 14 15 for i in range(0, times): 16 if speed_gap < 1: #如果速度间隔小于1,那么就会强制生成一个最高速和最低速度之间的一个速度 17 data_array[i] = random.random() * max_speed 18 else: 19 data_array[i] = random.randint(0, max_speed / speed_gap) * speed_gap #随机生成一个最高速和最低速之间的速度,先除以speed_gap然后乘以speed_gap进行离散化 20 # array([130., 140., 65., 20., 125., 15., 65.,...] 60个 21 data_frame = pd.DataFrame(data_array) # 格式化 22 bin_range = np.arange(0, 200, speed_gap) # 设置横坐标区间 0-200 间隔为:5 23 data_frame.plot(kind = 'hist', bins = bin_range, legend = False) #获取时速统计次数的直方图 24 data_frame.plot(kind = 'hist', bins = bin_range, legend = False, weights = weights_array, ).set_ylabel("Probability") #获取时速统计概率的直方图 25 plt.show() 26 27 check_speed(1, 5, 60, 0, 200)
生成的速度数据直方图:
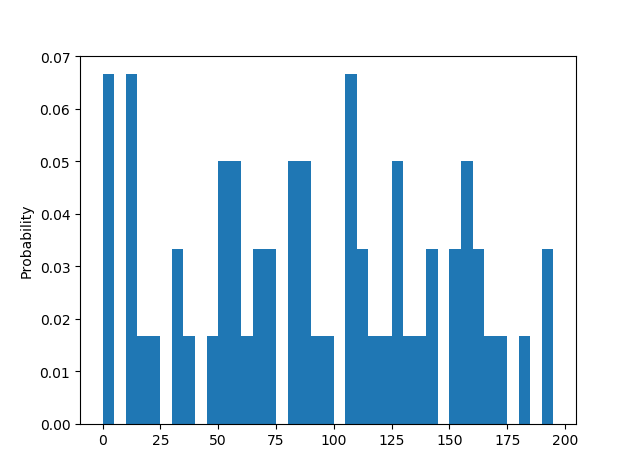

第二次模拟,假设我们把车升级到当今的主流车,仪表盘的最小刻度已经到 1 了,然后时间维度上,我们细分到 0.1 分钟,那么 1 小时我们将生成 600 个数据。我们还可以进行第三次、第四次、甚至是无穷次的模拟,每次模拟的时候我们都将行驶速度的精度进一步提升、将时间间隔进一步缩小,让两者都趋近于 0,那么我们的模拟就从离散逐步趋近于连续的值了。

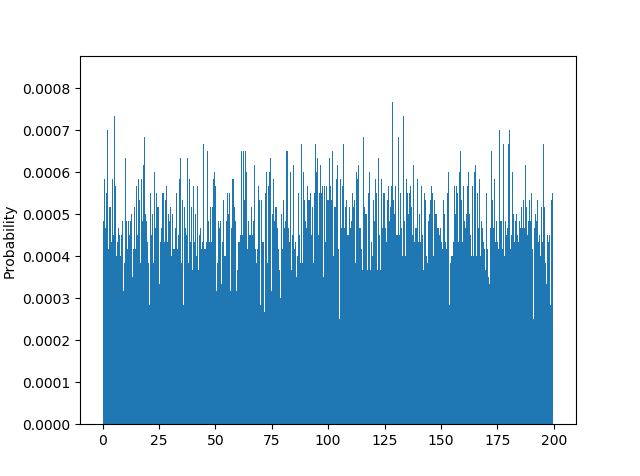 、
、
上面通过两个模拟实验,分别展示了离散型和连续型概率的分布。其实,人们在实际运用中,已经总结出了一些概率分布,这里挑几个最常见的进行讲解。
常用的离散分布有伯努利分布、分类分布、二项分布、泊松分布等等,这里我重点介绍两个。
1. 伯努利分布
第一个是伯努利分布(Bernoulli Distribution),这是单个随机变量的分布,而且这个变量的取值只有两个,0 或 1。伯努利分布通过参数λ来控制这个变量为 1 的概率。

或者写作:
![]()
另一个是分类分布(Categorical Distribution),也叫 Multinoulli 分布。它描述了一个具有 k 个不同状态的单个随机变量。这里的 k,是有限的数值,如果 k 为 2 的时候,那么分类分布就变成了伯努利分布
2. 正态分布
离散型随机变量的状态数量是有限的,所以可以通过伯努利和分类分布来描述。可是对于连续型随机变量来说,状态是无穷多的,这时我们就需要连续分布模型。比较经典的连续分布有正态分布、均匀分布、指数分布、拉普拉斯分布等等。如果你只需要掌握一个的话,那肯定是正态分布。
正态分布(Normal Distribution),也叫高斯分布(Gaussian Distribution)。我把这个分布的公式列在这里
这个分布可以近似表示日常生活中很多数据的分布,我们经常使用它进行机器学习的特征工程,对原始数据实施标准化,使得不同范围的数据具有可比性。所以,如果想要学习机器学习,一定要掌握正态分布。

在这个公式中有两个参数,μ表示均值,σ表示方差。看这个公式不太直观,我们来看一看对应的分布图。
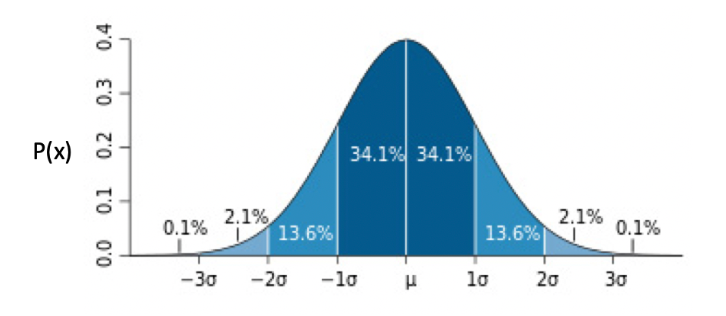
从这个图可以看出,越靠近中心点μ,出现的概率越高,而随着渐渐远离μ,出现的概率先是加速下降,然后减速下降,直到趋近于 0。蓝色区域上的数字,表示了这个区域的面积,也就是数据取值在这个范围内的概率。例如,数据取值在[-1σ, μ]之间的概率为 34.1%。
现实中,很多数据分布都是近似于正态分布的。例如人类的身高体重。拿身高来说,大部分人都是接近平均值身高,偏离平均身高越远,相对应的人数越少。这也是为什么正态分布很常用的原因。
很多数据分布都是近似于正态分布的。例如人类的身高体重。拿身高来说,大部分人都是接近平均值身高,偏离平均身高越远,相对应的人数越少。这也是为什么正态分布很常用的原因。
期望值
期望值,也叫数学期望,是每次随机结果的出现概率乘以其结果的总和。如果我们把每种结果的概率看作权重,那么期望值就是所有结果的加权平均值。它在我们的生活中十分常见,例如计算多个数值的平均
离散型的更容易理解,打个形象的例子,开门做生意,假设每条有三种可能,一种是生意满堂,一天能有10万的收入,一种是一半客人,一天收入只有5万,最后一种是没人来,一天收入为0,那么问每天收入“预期”是多少?由于有三种情况,我们不能直接说10万、5万还是0,只能看三种情况出现的概率分别是多少?如果客满的概率是1.0,其他两种是0.0,那么一天的收入是10*1.0=10万,如果客满的概率是0.5, 半客满的概率是0.3,没人的概率是0.2,那么一天收入的“期望”就是10*0.5+5*0.3+0*0.2 = 6.5万值,其实就是求期望值,只不过我们假设每个数值出现的概率是相同的。