tarjian（lca模板）

http://poj.org/problem?id=1330

题意：给出一颗n个节点的树，n-1条边表示u是v的父节点。询问a与b的最近公共祖先

解法：tarjian：

1、找出根节点（无父节点）从根点开始dfs遍历图，直到遍历该节点已经没有可访问的点为止

2、回溯，将v与u合并（注意u与v的父子关系）

3、询问与u有关的所有点是否访问，如访问则find（v）即为u与v的lca。

温故知新：可以想到，trajan算法实现利用dfs的特性与最近公共祖先的特性，当遍历到某u节点时，假设V为u结点的左右子树结点的集合，

当dfs遍历完V集合回溯到u时，V集合的最近公共祖先即为u ，所以可以使用并查集。

所以可以看成该模型（可能去除树上面）

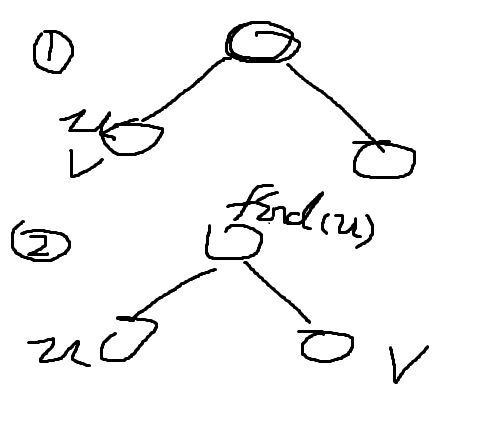
1、要么在同一侧，则lca = u。

2、要么在两侧，当u访问过后，访问到v，则lca = find（u）

#include <bits/stdc++.h>
using namespace std;
const int N = 40010, M = 80010;
int f[N], n, q, cnt[N];//并查集、离线记录答案
int e[M], ne[M], h[N], idx;
bool vis[N];//标记已经访问过的点
struct node
{
    int x, y;
    node(int _x, int _y) { x = _x, y = _y; }
};
vector<node> g[N];//链表储存需要查询两点

void add(int a, int b) { e[idx] = b, ne[idx] = h[a], h[a] = idx++; }
int find(int x) { return x == f[x] ? f[x] : f[x] = find(f[x]); }
void unite(int a, int b)
{
    a = find(a), b = find(b);
    if (a == b)
        return;
    f[a] = b;
}
void trajan(int u)
{
    vis[u] = 1 ;
    for (int i = h[u]; ~i; i = ne[i])
    {
        int j = e[i];
        if(vis[j]) continue;
        trajan(j);
        unite(j, u);
        vis[j] = 1;
    }
    for (auto i : g[u])
    {
        if (vis[i.x])//如果另一个点已经访问过
        {
            int fa = find(i.x);//根据dfs特性，lca就为另一个结点的集合的根节点
            cnt[i.y] = fa;
        }
    }
}
int rt;
int main()
{
    #ifdef ONLINE_JUDGE
    #else
        freopen("D:\c++\in.txt", "r", stdin);
        //freopen("D:\c++\out.txt", "w", stdout);
    #endif
    memset(h, -1, sizeof(h));
    for (int i = 1; i <= 40000; i++)
        f[i] = i;
    cin >> n;
    for (int i = 1; i <= n; i++)
    {
        int a, b;
        cin >> a >> b;
        if (b == -1)
        {
            rt = a;
            continue;
        }
        add(a, b);
        add(b, a);
    }
    cin >> q;
    for (int i = 1; i <= q; i++)
    {
        int a , b ;
        cin >> a >> b ;
        g[a].push_back({b, i});
        g[b].push_back({a, i});
    }
    trajan(rt);
    for (int i = 1; i <= q; i++)
    {
        cout << cnt[i] << endl;
    }
}