树

线性表，栈和队列都属于线性结构，而树，图属于非线性结构。

宏观树

树

• 每个节点有零个或多个子节点
• 没有父节点的节点被称为根节点
• 每个非根节点只能有一个父节点

应用：层级的文件系统

二叉树

在树的基础上，增加限制条件：每个节点最多含有两个子节点。

二叉树的三种遍历方式：

• 先序遍历

  先访问根节点，然后访问左节点，最后访问右节点(根->左->右)

• 中序遍历

  先访问左节点，然后访问根节点，最后访问右节点(左->根->右)

• 后序遍历

  先访问左节点，然后访问右节点，最后访问根节点(左->右->根)

二叉查找树

在二叉树的基础上，增加限制条件：

• 左子树节点的值 > 根节点的值 > 右子树节点的值（对于任意节点来说）
• 没有键值相等的节点

二叉查找树相比于其他数据结构的优势在于查找、插入的时间复杂度较低为 O ( log ⁡ n ) 。二叉查找树是基础性数据结构，用于构建更为抽象的数据结构，如集合、多重集、关联数组等。

平衡二叉树

在二叉查找树的基础上，增加限制条件：每个节点的左子树和右子树高度差至多为1。

红黑树

在平衡二叉树的基础上，增加限制条件：

• 每个节点有红色，黑色两种选项
• 根节点和叶子节点必须是黑的
• 如果一个节点是红的，那么它的两个儿子都是黑的（红子黑）
• 任意节点到叶子节点NIL都包含相同数目的黑色节点

红黑树是一种应用很广的数据结构，如在Java集合类中TreeSet和TreeMap的底层，C++STL中set与map，以及linux中虚拟内存的管理。

哈夫曼树

也称最优二叉树。

最优体现在树的带权路径长度最小：（叶子节点的权值 和 叶子节点到根节点的路径长度的乘积 ）*所有叶子节点

哈夫曼树特征：权值小的节点远离根节点，权值大的节点靠近根节点。

B树

BTree也称为平衡多路查找树

B-Tree是为磁盘等外存储设备设计的一种平衡查找树。

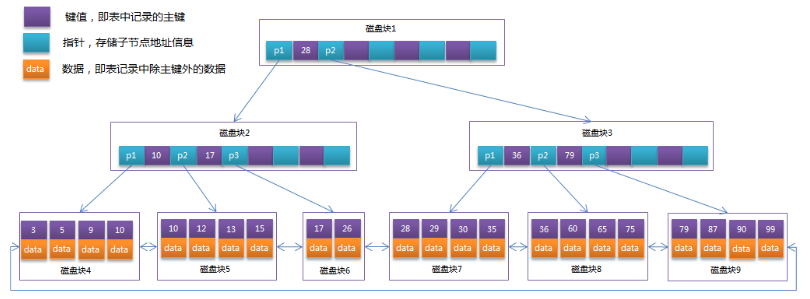
B+Tree

B+Tree是在B-Tree基础上的一种优化

• 非叶子结点只存储键值信息，不存储数据
• 所有的叶子结点都有一个链指针
• 数据记录都存放在叶子结点中

代码实现

二叉树代码实现（递归）

package com.company;

public class BinaryTree {

    private BinaryTree  leftNode;
    private BinaryTree  rightNode;
    private Integer value;

    public BinaryTree(Integer value) {
        this.value = value;
    }

    public BinaryTree getLeftNode() {
        return leftNode;
    }

    public void setLeftNode(BinaryTree leftNode) {
        this.leftNode = leftNode;
    }

    public BinaryTree getRightNode() {
        return rightNode;
    }

    public void setRightNode(BinaryTree rightNode) {
        this.rightNode = rightNode;
    }

    public Integer getValue() {
        return value;
    }

    public void setValue(Integer value) {
        this.value = value;
    }


    //先序遍历
    public void preTraverseBTree(BinaryTree rootNode)
    {

        if(rootNode!=null)
        {
            System.out.println(rootNode.value);

            preTraverseBTree(rootNode.getLeftNode());

            preTraverseBTree(rootNode.getRightNode());
        }
    }

    //中序遍历
    public void inTraverseBTree(BinaryTree rootNode)
    {

        if(rootNode!=null) {
            inTraverseBTree(rootNode.getLeftNode());

            System.out.println(rootNode.value);

            inTraverseBTree(rootNode.getRightNode());
        }
    }

    //后序遍历

    public void afterTraverseBTree(BinaryTree rootNode)
    {

        if(rootNode!=null) {
            inTraverseBTree(rootNode.getLeftNode());

            inTraverseBTree(rootNode.getRightNode());

            System.out.println(rootNode.value);
        }
    }
    

    public static void main(String[] args) {
        BinaryTree node1 = new BinaryTree(1);
        BinaryTree node2 = new BinaryTree(2);
        BinaryTree node3 = new BinaryTree(3);
        BinaryTree node4 = new BinaryTree(4);
        BinaryTree node5 = new BinaryTree(5);
        BinaryTree node6 = new BinaryTree(6);
        BinaryTree node7 = new BinaryTree(7);

        node1.setLeftNode(node2);
        node1.setRightNode(node3);

        node2.setLeftNode(node4);
        node2.setRightNode(node5);

        node3.setLeftNode(node6);
        node3.setRightNode(node7);

        System.out.println("先序遍历：");
        node1.preTraverseBTree(node1);

        System.out.println("中序遍历：");
        node1.inTraverseBTree(node1);

        System.out.println("后序遍历：");
        node1.afterTraverseBTree(node1);

    }
}

动态创建二叉查找树

参考：

数据结构之树