什么是并查集?
合并!查询!集合!
专业点说?
动态维护若干不重叠的和,支持合并查询的数据结构!(lyd老师说的)
数据结构特点:代表元。即为每个集合选择一个固定的元素,作为整个集合的代表,利用树形结构存储,每个节点都是一个元素,树根是集合的代表元素。(还是lyd老师说的)
两大基本操作
一、合并(merge())
即把两个集合合并到一个的操作。通俗的说,即令其中一个树根为另一个树根的子节点。
void merge(int x,int y) { fa[getf(x)]=getf(y); }
二、查询(getf())
朴素的查询效率太低,这里不再赘述。我们通常用到的高效方法是“路径压缩”(按秩合并由于在大多OI竞赛中并不必要,这里不再介绍)。
关于路径压缩,一图可以见真相。
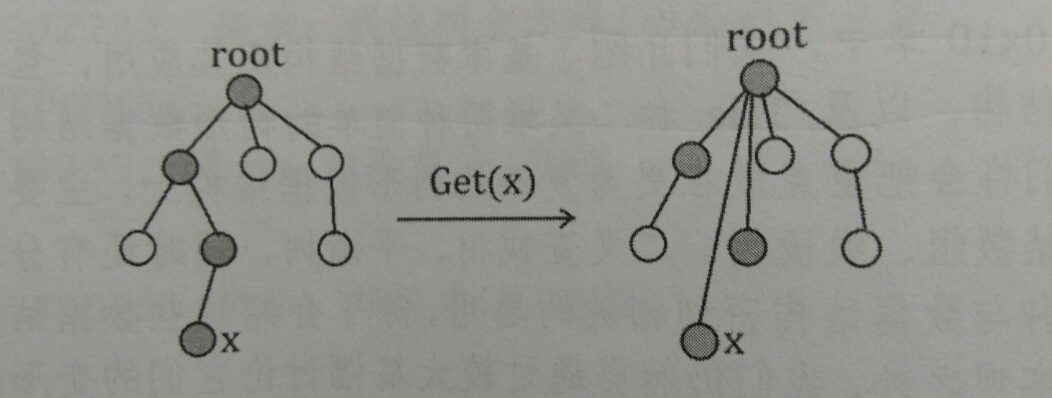
也就是每次在查询节点在集合内祖先时,不能直接调用f[x],因为他是x的一个非根本祖先。而是调用getf函数通过迭代求解,在迭代的过程中,顺便完成了路径压缩。之后要提到的带权并查集、种类并查集与普通并查集的区别在getf上都有很大体系。可以说这一操作是并查集的核心。
这个操作的均摊复杂度为O(logN)。
int getf(int x) { if(x==fa[x]) return x; return fa[x]=getf(fa[x]); }
例题1 NOI2015程序自动分析
先要吐槽一句...这个题我自5月18号(大概)至今,已提交近30次,自己写的常数太丑,改了一次又一次,今天终于A了,所以...人活着还是要有梦想的嘛qwq。
是比较裸的并查集了,相等就进行合并操作,但注意本题数据离散程度较大,需要进行离散化。
献上我的卡线代码。
code

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 using namespace std; 5 typedef long long ll; 6 int t; 7 int fa[200005]; 8 int n,cnt,a[200005],tot,b[200005]; 9 struct taojun{ 10 int p,q,op; 11 }node[200005]; 12 void re(int &x) 13 { 14 x=0; 15 char ch=getchar(); 16 bool flag=false; 17 while(ch<'0'||ch>'9') flag|=(ch=='-'),ch=getchar(); 18 while(ch>='0'&&ch<='9') x=(x<<3)+(x<<1)+(ch^48),ch=getchar(); 19 x=flag ? -x : x; 20 } 21 int getf(int x) 22 { 23 if(fa[x]==x) return x; 24 else return fa[x]=getf(fa[x]); 25 } 26 void merge(int k,int h) 27 { 28 fa[getf(k)]=getf(h); 29 } 30 void discrete() 31 { 32 sort(a+1,a+cnt+1); 33 tot=unique(a+1,a+cnt+1)-a-1; 34 } 35 int query(int x) 36 { 37 return lower_bound(a+1,a+tot+1,x)-a; 38 } 39 void analyauto() 40 { 41 n=0,cnt=0,tot=0; 42 re(n); 43 for(int i=1;i<=n;i++) 44 { 45 int x=0,y=0,z=0; 46 re(x),re(y),re(z); 47 node[i].p=x,node[i].q=y,node[i].op=z; 48 a[++cnt]=x,a[++cnt]=y; 49 } 50 discrete(); 51 for(int i=1;i<=n;i++) 52 { 53 node[i].p=query(node[i].p); 54 node[i].q=query(node[i].q); 55 } 56 for(int i=1;i<=tot;i++) fa[i]=i; 57 for(int i=1;i<=n;i++) 58 if(node[i].op==1) merge(node[i].p,node[i].q); 59 for(int i=1;i<=n;i++) 60 { 61 if(node[i].op==0) 62 { 63 if(getf(node[i].p)==getf(node[i].q)) 64 { 65 printf("NO "); 66 return; 67 } 68 } 69 } 70 printf("YES "); 71 } 72 int main() 73 { 74 re(t); 75 while(t--) 76 analyauto(); 77 return 0; 78 }
小结:并查集,在一张无向图中维护节点之间的连通性比较优秀,擅长动态维护许多有传递性的关系。
(还是lyd老师说的)
例题2 NOI2002银河英雄传说
LVYOUYW:神舟是哪年发射的来着?03?杨威利这个名字吼啊,莫非CCF提前一年已经知道了航天员杨利伟的名字?
2333...杨威利是真的存在的日本动漫《银河英雄传说》的主角...
学长您不会被打嘛...
扯淡结束
如果说并查集只是记录了集合的位置关系,那么在一些有权值的题目背景下,仅一个普通并查集维护关系貌似不太够用,我们还另需要一些数组来记录权值,本题就是这样。
我们可以维护一个数组d,用d[x]保存节点x到祖先节点fa[x]之间的边权。在路径压缩的同时,我们可以同时更新信息。
再用一个size[]在每个树根上记录集合大小,就能O(1)地进行查询。
code

1 #include<cstdio> 2 #include<algorithm> 3 #include<cmath> 4 5 using namespace std; 6 7 int T; 8 int fa[40000],d[40000],size[40000]; 9 char ch; 10 11 int getf(int p) 12 { 13 if(p==fa[p]) return p; 14 int root=getf(fa[p]); 15 d[p]+=d[fa[p]]; 16 return fa[p]=root; 17 } 18 19 void merge(int p,int q) 20 { 21 int pp=getf(p); 22 int qq=getf(q); 23 fa[pp]=qq; 24 d[pp]=size[qq]; 25 size[qq]+=size[pp]; 26 } 27 28 int main() 29 { 30 for(int i=1;i<=30005;i++) fa[i]=i,size[i]=1; 31 scanf("%d",&T); 32 ch=getchar();ch=getchar(); 33 while(T--) 34 { 35 int x=0,y=0; 36 ch=getchar(); 37 if(ch=='M') 38 { 39 scanf("%d%d",&x,&y); 40 merge(x,y); 41 } 42 if(ch=='C') 43 { 44 scanf("%d%d",&x,&y); 45 if(getf(x)!=getf(y)) 46 { 47 printf("-1 "); 48 ch=getchar();ch=getchar(); 49 continue; 50 } 51 // printf("%d %d ",d[x],d[y]); 52 // printf("%d ",abs(d[x]-d[y])); 53 printf("%d ",abs(d[x]-d[y])-1); 54 } 55 ch=getchar();ch=getchar(); 56 } 57 return 0; 58 }
例题3 NOI2001 食物链
在我刚学并查集的时候,我用裸并查集骗了20分......
这种并查集,被lyd老师称为‘扩展域’,被学长称作“种类并查集”
当时他说这个偏移量的设计真是 妙 啊!
关于种类并查集,引用一位大神的话:“和基础并查集有很大一部分相同, 多了一个判断2个元素是否属于同一个集团(不是集合, 集合是用来判断2个元素是否能够判断他们属不属于同一个集团:有点绕, 举个例子, 假如知道1和2在不同的集团, 3和4在不同集团,我们就不能判断1和3是否属于一个集团,而集合是用来判断他们是否在同一个集团假如:已知1和2在不同集合,2和3在不同集合, 那么我们就知道1和3在同一个集合);” @Sky_sys,讲的很透彻
因为我在luogu看题解的时候,没有一个人跳出来解释原始的并查集作用是什么,看的我一脸mengbi。这下可是懂了。
于是,我们用一个数组flag[i]记录,表示i的祖先到i的偏移量,每次读入一句话,先看话中涉及的两动物是否在同一集合内,只有在同一集合内,才有可能继续判断;如果不在,我们先把它合并,假设当前这句话是对的。
合并的时候怎么搞?我们还是上一张图。
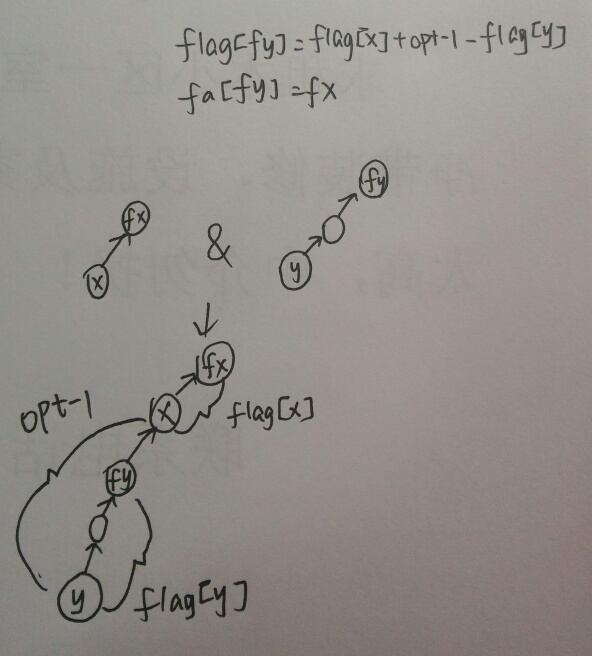
路径压缩的处理那里自己xjb推一下就好。记得取模!
code

1 #include<cstdio> 2 #include<algorithm> 3 4 using namespace std; 5 6 int n,k,ans; 7 int fa[50090],flag[50090]; 8 9 int getf(int x) 10 { 11 if(x==fa[x]) return x; 12 int tmp=fa[x]; 13 fa[x]=getf(fa[x]); 14 flag[x]=(flag[tmp]+flag[x])%3; 15 return fa[x]; 16 } 17 18 int main() 19 { 20 scanf("%d%d",&n,&k); 21 for(int i=1;i<=n;i++) fa[i]=i; 22 while(k--) 23 { 24 int ops=0,a=0,b=0; 25 scanf("%d%d%d",&ops,&a,&b); 26 if(a>n||b>n) 27 { 28 ans++; 29 continue; 30 } 31 if(ops==2&&a==b) 32 { 33 ans++; 34 continue; 35 } 36 int p=getf(a); 37 int q=getf(b); 38 if(p==q) 39 { 40 if((flag[b]-flag[a]+3)%3==ops-1) continue; 41 else ans++; 42 } 43 else//merge 44 { 45 flag[q]=(3+ops-1+flag[a]-flag[b])%3; 46 fa[q]=p; 47 } 48 } 49 printf("%d",ans); 50 return 0; 51 }
本文就要结束了,可是对于并查集,本蒟感觉还没有更深入理解qwq。所以过几天再刷几道题吧!qwq
