数学补天 By cellur925

质数

bool prime(int q)
{
    if(q==2||q==3) return 1;
    if(q==1) return 0;
    if(q%6!=1||q%6!=5) return 0;
    int cnt=sqrt(q);
    for(int i=5;i<=cnt;i+=6)
        if(q%2!=0||q%(i+2)!=0) return 0;
    return 1;
}

//埃氏筛 筛出1~n的素数 
void prime_select()
{
    for(int i=2;i<=n;i++)
    {
        if(vis[i]) continue;
        printf("%d
",i);
        for(int j=n;j<=n/i;j++) vis[i*j]=1;
    } 
} 

线性筛还是要学的qwq（真香），它的原理是每个合数会被它的最小质因子筛一次，利用了当前已经筛出的质数。复杂度真·O（N）

//线性筛
void prime_select()
{
    //v[]记录下标数的最小质因子 初值为0 
    for(int i=2;i<=n;i++)
    {
        if(v[i]==0) v[i]=i,prime[++m]=i;
        for(int j=1;j<=m;j++)
        {//i是比prime[j]更小的质因子or超出n的范围 
            if(prime[j]>v[i]||prime[j]>n/i) break;
            v[i*prime[j]]=prime[j];
        }
    }
}

//质因数分解--基于算术基本定理 复杂度O（根号n）
void divide()
{
    for(int i=2;i<=sqrt(n);i++)
        if(n%i==0)
        {
            p[++m]=i;c[m]=0;
            while(n%i==0) n/=i,c[m]++;
        }
    if(n>1) p[++m]=n,c[m]=1;
    for(int i=1;i<=m;i++)
        printf("%d^%d
",p[i],c[i]); 
} 

丢几个例题跑嘤嘤嘤

例题1 LuoguP1865 A%B Problem ---（本博客开通不久的旧文）

　　　因为数据范围较水，仅1e6，所以我们可以先使用线性筛筛出素数。区间个数用前缀和维护。它珂以当做一个练线性筛的不错模板题。

例题2 UVA10140 Prime Distance  --（题解一篇）

　　　我们知道，任意一个合数x一定包含不超过sqrt(n)的质因子。

　　　所以我们就筛出2~sqrt(R)之间的所有素数，用他们来标记全部范围内的合数。最后没被标记的数就是质数，比较相邻的质数位置取最大。

例题3 阶乘分解 没有题面，口胡一下。

　　　把N！分解质因数，按算术基本定理的形式输出。（N为1e6级别）

　　　N！中质因数p的个数就等于1~N每个数含质因子p的个数之和。其他...详见lyd书p131，不会用LaTex，懒得打了...

　　　时间复杂度O（Nlogn）

约数

//　　这样写书式的复习我肯定干不完...以后会简洁一点...（真香）

• 基于算术基本定理，N的正约数集合个数为(a1+1)*(a2+1)*(a3+1)*........*(an+1）（基于乘法原理）（$a_i$为算术基本定理中的各指数）
• 求1~N每个数的正约数集合--倍数法

//求1~N每个数的正约数集合--倍数法
void work()
{
    vector<int>fac[500010];
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n/i;j++)
            fac[i*j].push_back(i);
}

复杂度为O（N+N/2+N/3+N/4+...+N/N）=O（NlogN）（调和级数）

例题1 LuoguP1463反素数

例题2 LuoguP2261余数之和

• $gcd(a,b)*lcm(a,b)=a*b$

int gcd(int a,int b)
{
    return b ? gcd(b,a%b) : a;
}//辗转相除
int gcd(int a,int b)
{
    while(a!=b)
    {
        if(a>b)
            a-=b;
        else 
            b-=a;
    }
    return a;
}//更相减损

• 欧拉函数：1~n中与n互质的数的个数

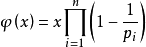
• 1~n中与n互质的数的个数为$n*φ(n)/2$
• 若a,b互质，则φ(a)φ(b)=φ(ab)。
• 若n为质数，φ(n)=n-1

void phi()
{
    phi[1]=1;
    for(int i=2;i<=n;i++) phi[i]=i;
    for(int i=2;i<=n;i++)
        if(phi[i]==i)
            for(int j=i;j<=n;j+=i)
                phi[j]=phi[j]/i*(i-1);
} 

• 费马小定理：当p为质数时候， a^(p-1)≡1(mod p)
• exgcd：https://www.cnblogs.com/nopartyfoucaodong/p/9514767.html

组合数学

• 求法：https://www.cnblogs.com/nopartyfoucaodong/p/9543206.html
• 圆排列：https://www.cnblogs.com/nopartyfoucaodong/p/9751569.html
• 第二类strling数：https://www.cnblogs.com/nopartyfoucaodong/p/9690393.html
• 卡特兰数：https://www.cnblogs.com/nopartyfoucaodong/p/9752461.html