这位dalao的单调栈文章很棒!我写的是他的题单233. http://www.cnblogs.com/COLIN-LIGHTNING/p/8474668.html
一、单调栈的一般写法
for(int i=1;i<=n;i++) { int x=0; scanf("%d",&x); while(x>=sta[top]&&top) top--; sta[++top]=x; }
而各种各样繁杂的题目正是在这个基础上维护一些其他的信息。
二、注意事项
栈不能为空。要随时注意,否则RE。
计数类可能会用到$longlong$。
三、例题详解
例题0 LIS(最长上升子序列)辣个$nlogn$的算法其实本质上就是单调栈...
例题1 音乐会的等待
N个人正在排队进入一个音乐会。人们等得很无聊,于是他们开始转来转去,想在队伍里寻找自己的熟人。队列中任意两个人A和B,如果他们是相邻或他们之间没有人比A或B高,那么他们是可以互相看得见的。
写一个程序计算出有多少对人可以互相看见。(注意,是互相看见)
维护一个单调不增的栈。(因为两个之间没有比他们高的人时他们才能互相看见,中间隔等高个人时是可以互相看见的)
(注意!脑子别晕!233,这是栈!不是队列!栈顶是最后加的!)
当新来的人身高小于栈顶,直接进来。答案在栈非空的情况下加1,这算的是栈顶和当前元素这对。(满足相邻的条件)
当新来的人身高大于栈顶,弹栈直到满足小于(或等于)。因为维护的单调递减的栈,而新生还很高,所以自然能看得见。这里每次弹栈都加上那个元素的个数(具体接下来会讲)。满足性质后,再和栈顶比较。
当新来的人身高等于栈顶,弹栈直到小于。我们把和它相等的都弹走,但是要注意记上和它相等的数出现的次数,以便之后使用,因为相等,所以肯定看的见,为接下来记录了信息(解释了第二种情况)。满足性质后,再和栈顶比较。
综上,我们看出每个元素最多入栈出栈一次,复杂度$O(N)$,每次入栈后,都要在栈不为空的情况下,答案++,因为栈顶(最外面的元素)一定能看见新来的元素。
Code

1 #include<cstdio> 2 #include<algorithm> 3 4 using namespace std; 5 typedef long long ll; 6 7 int n,top,x,num; 8 struct node{ 9 int val,num; 10 }sta[500090]; 11 ll ans; 12 13 int main() 14 { 15 scanf("%d",&n); 16 for(int i=1;i<=n;i++) 17 { 18 scanf("%d",&x); 19 node p=(node){x,1}; 20 while(x>=sta[top].val&&top) 21 { 22 ans+=sta[top].num; 23 if(sta[top].val==x) p.num+=sta[top].num; 24 //虽然弹走了 记下 以后用得到 25 top--; 26 } 27 if(top) ans++; 28 sta[++top]=p; 29 } 30 printf("%lld",ans); 31 return 0; 32 }
Byteburg市东边的建筑都是以旧结构形式建造的:建筑互相紧挨着,之间没有空间.它们共同形成了一条长长的,从东向西延伸的建筑物链(建筑物的高度不一).Byteburg市的市长Byteasar,决定将这个建筑物链的一侧用海报覆盖住.并且想用最少的海报数量,海报是矩形的.海报与海报之间不能重叠,但是可以相互挨着(即它们具有公共边),每一个海报都必须贴近墙并且建筑物链的整个一侧必须被覆盖(意思是:海报需要将一侧全部覆盖,并且不能超出建筑物链,即不能盖着没有海报存在的地方)
读完题后,我们很快就会发现,那个宽度的条件其实是没用的,我们只需要考虑高度就行了。设开始我们需要海报的数量等于矩形的数量,我们再一点点减。那么,我们便可以维护一个高度单调递增的栈,在弹栈过程中,若遇到和自己相等的高度,就将答案减去1,因为如图,我们可以横着盖,我们只需要再把高出来的(於出来的)用一张海报即可。

Code

1 #include<cstdio> 2 #include<algorithm> 3 4 using namespace std; 5 6 int n,ans,top; 7 int sta[300000]; 8 9 int main() 10 { 11 scanf("%d",&n); 12 for(int i=1;i<=n;i++) 13 { 14 int y=0,x=0; 15 scanf("%d%d",&y,&x); 16 while(top&&x<=sta[top]) 17 { 18 if(x==sta[top]) ans++; 19 top--; 20 } 21 sta[++top]=x; 22 } 23 printf("%d",n-ans); 24 return 0; 25 }
以上都是一些比较简单的线性问题。接下来我们要看的是那些或者在二维上,或者掺杂入实际的面积,这些更复杂的问题。
例题3 玉蟾宫 哎又要看Freda学姐和rainbowcat虐狗了
其实这题还有悬线法,是求最大子矩阵的一个方法,这里就不再说了==(大坑)
抽象一下本题的模型:有障碍点的情况下的最大子矩形。
虽然这题是二维的了,但是我们还可以分别计算情况。
首先,我们用一个$f[i][j]$表示在$(i,j)$点,前$i$行,第$j$列,以第$i$行结尾,连续的‘F’个数。(最大可延伸距离)
行与行之间的问题就解决了。
然后在同一行,不同列上的问题就可以用单调栈(单调递增栈)来维护了。
单调栈中存储两个信息。此单位高度$height$,和对应可控宽度$wid$(对应可控我觉得说的非常准确)
同理,我们当前的高度(f数组)大于栈顶时,直接把它压入栈。
否则,就一直弹栈。弹栈的时候,我们要记录矩形的信息来更新答案。它的$wid$是所有弹栈元素的$wid$+1.(因为我们继承了之前的信息,这部分 到之后也是可以用的。因为被弹栈的元素高度均大于当前元素,在可控范围内。)
之后更新答案即可。枚举到最后一列后,把栈都搞空。
Code

1 #include<cstdio> 2 #include<algorithm> 3 4 using namespace std; 5 6 int n,m,ans,top,tmp,neww; 7 struct node{ 8 int height,wid; 9 }sta[2000]; 10 char qwq[5],mapp[2000][2000],f[2000][2000]; 11 12 void work(int x) 13 { 14 top=1;tmp=0;neww=0; 15 sta[1].height=f[x][1]; 16 sta[1].wid=1; 17 for(int i=2;i<=m;i++) 18 { 19 tmp=0; 20 while(f[x][i]<=sta[top].height&&top) 21 { 22 tmp+=sta[top].wid; 23 neww=max(neww,tmp*sta[top].height); 24 top--; 25 } 26 sta[++top].height=f[x][i]; 27 sta[top].wid=tmp+1; 28 } 29 tmp=0; 30 while(top) 31 { 32 tmp+=sta[top].wid; 33 neww=max(neww,tmp*sta[top].height); 34 top--; 35 } 36 ans=max(ans,neww); 37 } 38 39 int main() 40 { 41 scanf("%d%d",&n,&m); 42 for(int i=1;i<=n;i++) 43 for(int j=1;j<=m;j++) 44 { 45 scanf("%s",qwq+1),mapp[i][j]=qwq[1]; 46 if(mapp[i][j]=='F') f[i][j]=f[i-1][j]+1; 47 } 48 for(int i=1;i<=n;i++) work(i); 49 printf("%d",ans*3); 50 return 0; 51 }
例题4 Largest Rectangle in a Histogram
在一条水平线上给出若干连续矩形,求包含于这些矩形的并集内部最大矩形的面积。
这应该是单调栈的典型题目惹qwq。
我们假设,到现在为止,读入的矩形高度都是递增的,那么如果突然读入了一个比上一个矩形矮的矩形,那么之前高的矩形搞出来就没有用了(於出来了)
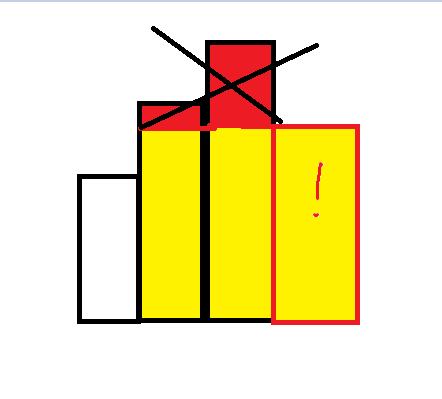
打叉的部分就没用了。没用就删去啊,所以我们在做的事情就是维护一个单调递增的矩形序列。与上题相似,弹矩形的时候,我们同样要维护弹出矩形的答案。
其实这和上一题差不多啦qwq。
Code

1 #include<cstdio> 2 #include<algorithm> 3 #include<cstring> 4 5 using namespace std; 6 typedef long long ll; 7 8 int n,top,x,tmp; 9 ll ans; 10 struct node{ 11 int height,wid; 12 }sta[1000090]; 13 14 15 int main() 16 { 17 while(scanf("%d",&n)!=EOF&&n) 18 { 19 for(int i=1;i<=n;i++) 20 { 21 tmp=0; 22 scanf("%d",&x); 23 while(x<=sta[top].height&&top) 24 { 25 tmp+=sta[top].wid; 26 ans=max(ans,1ll*tmp*sta[top].height); 27 top--; 28 } 29 sta[++top].height=x; 30 sta[top].wid=tmp+1; 31 } 32 tmp=0; 33 while(top) 34 { 35 tmp+=sta[top].wid; 36 ans=max(ans,1ll*tmp*sta[top].height); 37 top--; 38 } 39 printf("%lld ",ans); 40 top=0;ans=0; 41 memset(sta,0,sizeof(sta)); 42 } 43 return 0; 44 }
这种更新面积(我也不知道怎么总结)的问题,最后一定要记得把栈搞空啊qwq。
单调栈先告一段落,下一次来看单调队列qwq。
