1.1.3 时间复杂度有哪些?如何计算程序的时间复杂度和空间复杂度,举例说明。
常见的空间复杂度
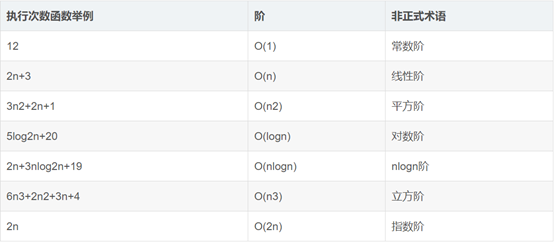
时间复杂度之间的大小关系

相关计算
时间复杂度例题

- 第一个for循环语句的频度为
n - 第二个for循环语句的频度为
n*log2n - 即第二个for循环语句是执行次数最多的语句
- 用大O表示时间复杂度
T(n) = O(n*log2n)
空间复杂度例题
一个算法的空间复杂度只考虑在运行过程中为局部变量分配的存储空间的大小:形参、局部变量
- 声明一个变量'O(1)'

- 声明一个一维数组'O(n)'
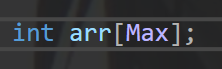
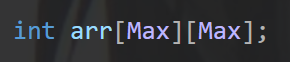
- 声明一个一维数组'O(n^2)'
1.2 线性表(1分)
1.2.1 顺序表
介绍顺序表结构体定义、顺序表插入、删除的代码操作
介绍顺序表插入、删除操作时间复杂度
顺序表结构体定义

顺序表的插入代码展示
void InsertSq(SqList& L, int x)//顺序表L中插入数据x
{
int j;
for(int i = 0;i<L->length;i++)
{
if (L->data[0] > x)//插入位置在第一个元素
{
L->length++;//顺序表长度加一
for (j = L->length - 1; j > 0; j--)
{
L->data[j] = L->data[j - 1];
}
L->data[0] = x;
break;
}
else if (L->data[i] <= x && L->data[i + 1] > x)//插入位置在表中间
{
L->length++;//顺序表长度加一
for (j = L->length - 1; j > i+1; j--)
{
L->data[j] = L->data[j - 1];
}
L->data[i+1] = x;
break;
}
else if (L->data[L->length - 1] <= x)插入数据在最后一个元素
{
L->length++;//顺序表长度加一
L->data[L->length - 1] = x;
break;
}
}
}
- 顺序表的插入中,第二个for循环语句是执行次数最多的语句,
T(n)=O(n^2)
顺序表的重复数据删除代码展示
void DelSameNode(List& L)//删除顺序表重复元素
{
for (int i = 0; i < L->length; i++)
{
for (int j = i + 1; j < L->length;)
{
if (L->data[i] == L->data[j])//找到重复数据
{
for (int k = j; k < L->length-1 ; k++)//将删除位置之后的数据顺位前移
{
L->data[k] = L->data[k + 1];
}
L->length--;//顺序表长度减一
continue;
}
j++;//当发现重复数据时j不要加一,因为将后面的数据循环前移,若直接加一,会导致重复数据的下一位数据不被判断
}
}
}
- 顺序表的删除中,第三个for循环语句是执行次数最多的语句,
T(n)=O(n^3)
1.2.2 链表(2分)
画一条链表,并在此结构上介绍如何设计链表结构体、头插法、尾插法、链表插入、删除操作
重构链表如何操作?链表操作注意事项请罗列。
链表及顺序表在存储空间、插入及删除操作方面区别,优势?
链表结构体

注意事项
- 建议用上述方式定义链表,但是此方法也需要理解
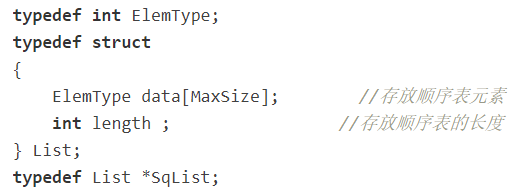
头插法

注意事项
- 要先把所需插入的结点node的next关系指向L->next,再改变L->next的指向,使其指向node
尾插法

注意事项
- 尾插法插入数据是通过改变尾指针r的next关系,需注意最后的尾结点一定要置空
链表插入、删除操作
插入

删除

注意事项
- 若程序中有对p->next做操作,while条件判断语句应为p->next!=NULL,否则会出现访问异常
- 仅改变要删除结点前后的next关系并不是真正的删除了结点,需要使用delete来彻底删除结点
重构链表
L=new LNode;//新建链表
p=L->next;//保存链表的后继关系
L->next=NULL;//重构链表
注意事项
- 要设置指针来保存链表的后继关系,不让其丢失
重点重点重点!!!
- 对链表进行操作前,都要先判定链表是否为空
判断链表是否为空的方法
-
带头结点(HL)的单链表
HL->next==NULL -
带头结点(HL)的循环单链表
HL->next==HL
链表及顺序表在存储空间、插入及删除操作方面区别,优势?
1.顺序表存储(数组)
- 优点:
(1)空间利用率高。
(2)存取速度高效,通过下标来直接存储。 - 缺点:
(1)插入和删除比较慢,比如:插入或者删除一个元素时,整个顺序表之后的数据需要遍历移动来重排。
(2)不可以增长长度,有空间限制,当需要存取的元素个数可能多于顺序表的元素个数时,会出现"溢出"问题,而当元素个数远少于预先分配的空间时,空间浪费大。
2.链表存储
- 优点:
(1)插入和删除速度快,且可以保留原有的物理顺序,不用遍历重排,只需要改变指针指向即可。
(2)没有空间限制,存储元素的个数无上限,基本只与内存空间大小有关,不会出现溢出的现象。 - 缺点:
(1)占用额外的空间以存储指针。
(2)查找速度慢,因为查找时,需要循环链表访问,需要从开始节点一个一个节点去查找元素访问。
总结
- 顺序表适用于做查找,而链表适用于插入删除。
1.2.3 有序表及单循环链表(1分)
有序顺序表插入操作,代码或伪代码介绍。
void InsertSq(SqList& L, int x)//顺序表L中插入数据x
{
int j;
for(int i = 0;i<L->length;i++)
{
if (L->data[0] > x)//插入位置在第一个元素
{
L->length++;//顺序表长度加一
for (j = L->length - 1; j > 0; j--)
{
L->data[j] = L->data[j - 1];
}
L->data[0] = x;
break;
}
else if (L->data[i] <= x && L->data[i + 1] > x)//插入位置在表中间
{
L->length++;//顺序表长度加一
for (j = L->length - 1; j > i+1; j--)
{
L->data[j] = L->data[j - 1];
}
L->data[i+1] = x;
break;
}
else if (L->data[L->length - 1] <= x)//插入数据在最后一个元素
{
L->length++;//顺序表长度加一
L->data[L->length - 1] = x;
break;
}
}
}
有序单链表数据插入、删除。代码或伪代码介绍。
void ListInsert(LinkList& L, ElemType e)//有序链表插入元素e
{
LinkList p, node;
p = new LNode;
node = new LNode;
node->data = e;
p = L->next;
//为空表
if (p == NULL)
return;
//不为空表
while (p->next != NULL)//此处条件应为p->next!=NULL,因为下一行有对p->next做操作,若其为NULL会出现访问异常
{
if (p->data <= e && p->next->data >e )//找到插入的位置
{
node->next = p->next;//改变要插入位置的前后位置的next关系
p->next = node;
return;
}
p = p->next;
}
//单独讨论,插入的数在链表末尾时
node->next = p->next;
p->next = node;
}
void ListDelete(LinkList& L, ElemType e)//链表删除元素e
{
LinkList p, q, s;
p = new LNode;
q = new LNode;
s = new LNode;
int flag = 0;
p = L;
q = L->next;//设置前后两个连续指针,方便后续移动删除
//为空表
if (q == NULL)
return;
//不为空表
while (q != NULL)
{
if (q->data == e)//找到要删除数
{
s = q;//保存结点
q = q->next;
p->next = q;//改变结点的前驱后继
delete s;//删除结点
flag = 1;//标记
return;
}
p = q;
q = q->next;
}
if (!flag)//没找到要删除数
{
cout << e << "找不到!" << endl;
}
}
有序链表合并,代码或伪代码。尽量结合图形介绍。
void MergeList(LinkList& L1, LinkList L2)
{
LinkList p1, p2,move;
p1 = L1->next;
p2 = L2->next;
move = L1;
//当为空表时,因为以L1为基础构建,所以不需要考虑L2为空的情况
if (p1 == NULL)
L1 = L2;
//不为空表
while (p1&& p2)//当两个链表均未遍历至最后一个结点
{
if (p1->data > p2->data )//p2小于p1
{
move->next = p2;
move = p2;
p2 = p2->next;
}
else if (p1->data < p2->data)//p2大于p1
{
move->next = p1;
move = p1;
p1 = p1->next;
}
else//p2等于p1,排除重复数据
{
move->next = p1;//任取p1,p2中的一个存入L1中,跳过另一个中的相同数据
move = p1;
p1 = p1->next;//p1,p2均后移
p2 = p2->next;
}
}
//一个链表已经遍历完成,另一个链表可能还有数据余下,全加入L1中
if (p1)
move->next = p1;//将p1中剩余的结点全部加入L1中
if(p2)
move->next = p2;//将p2中剩余的结点全部加入L1中
}
有序链表合并和有序顺序表合并,有哪些优势?
有序链表合并
- 不需要第三个链,可以直接在其中一个链上操作,通过改变每个结点的next关系,来达到排序与合并
有序顺序表合并
- 在有第三个顺序表的参与下才会更加方便,所以占用的空间较大,而且要考虑顺序表的长度大小,以免出现溢出的现象
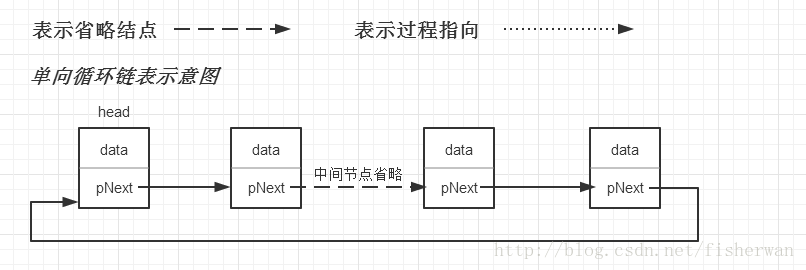
单循环链表特点,循环遍历方式?
- 特点:
1.可以从任何一个结点开始,向后访问到达任意结点。
2.最后一个结点指向头结点
- 循环遍历方式
通过将最后一个结点指向头结点来实现循环。
2.PTA实验作业(4分)
此处请放置下面2题代码所在码云地址(markdown插入代码所在的链接)。如何上传VS代码到码云
两个有序序列的中位数
#include <iostream>
#define max 100000
using namespace std;
typedef int ElemType;
typedef struct
{
ElemType data[max];
int length;
}List, * SqList;
void CreateList(SqList& S1, SqList& S2, int n);//创建顺序表
void MergeList(SqList& S1, SqList& S2,SqList& L);//合并顺序表
//int FindMed(SqList L);//寻找中位数
int main()
{
int n;
int Med;
SqList L,S1,S2;
cin >> n;//输入序列的公共长度
CreateList(S1, S2, n);//建立顺序表
MergeList(S1,S2,L);//合并顺序表
//FindMed(L);//寻找中位数
Med = L->data[(2 * n - 1) / 2];
cout << Med;
}
void CreateList(SqList& S1, SqList& S2, int n)
{
S1 = new List;
S2 = new List;
S1->length = n;
S2->length = n;
for (int i = 0; i < n; i++)
{
cin >> S1->data[i];
}
for (int i = 0; i < n; i++)
{
cin >> S2->data[i];
}
}
void MergeList(SqList& S1, SqList& S2, SqList& L)//合并顺序表
{
int i = 0;
int j = 0;
int k = 0;
L = new List;
L->length = 2*S1->length ;
while (i<S1->length && j < S2->length)//S1,S2均未遍历完成
{
if (S1->data[i] <= S2->data[j])//S1小于等于S2
{
L->data[k++]=S1->data[i++];
}
else if (S1->data[i] > S2->data[j])//S1大于等于S2
{
L->data[k++] = S2->data[j++];
}
}
while(i < S1->length)//S1未遍历完成
{
L->data [k++]=S1->data[i++];
}
while (j < S2->length)//S2未遍历完成
{
L->data[k++] = S2->data[j++];
}
}
一元多项式的乘法与加法运算
#include<iostream>
using namespace std;
typedef int ElemType;
typedef struct PNode {
int coef;//系数
int expn;//指数
struct PNode* next;
}*PolyList,PNode;
void CreatPolyn(PolyList& L, int n);//尾插法建链表
void AddPolyn(PolyList& LC, PolyList& LA, PolyList& LB);//多项式相加
void MulltiPolyn(PolyList& LC, PolyList LA, PolyList LB);//多项式相乘
void PrintPolyn(PolyList P);//输出结果
int main()
{
int n,m;
cin >> n;
PolyList L1,L2,P1,P2;
CreatPolyn(P1, n);//创建链表
cin >> m;
CreatPolyn(P2, m);//创建链表
MulltiPolyn(L1, P1, P2);//多项式相乘
PrintPolyn(L1);
cout << endl;
AddPolyn(L2,P1, P2);//多项式相加
PrintPolyn(L2);
return 0;
}
void CreatPolyn(PolyList& L, int n)//尾插法建链表
{
int x, y;
PolyList p, t;
L = new PNode;
L->next = NULL;
t = L;
for (int i = 1; i <= n; i++){
cin >> x >> y;
if (x) {//除去系数为零的情况
p = new PNode;
p->coef = x; p->expn = y;
t->next = p;
t = p;
}
}
t->next = NULL;
}
void PrintPolyn(PolyList P)//输出结果
{
if (!P->next) cout << "0 0";//链表为空
P = P->next;
while (P){
cout << P->coef << " " << P->expn;
P = P->next;
if (P != NULL) cout<<" "; //只有在指针域不为NULL时,才输出空格间隔开每个多项式。即在多项式末位没有空格
}
}
void AddPolyn(PolyList& LC, PolyList& LA, PolyList& LB)//多项式相加
{
PolyList l ,t,t1, t2;
LC = new PNode;
LC->next = NULL;
l = LC;
t1 = LA->next;
t2 = LB->next;
while (t1 && t2) {
t = new PNode;
if (t1->expn == t2->expn) {//指数相同
if(t1->coef + t2->coef!=0){
t->coef = t1->coef + t2->coef;
t->expn = t1->expn;
l->next = t;
l = t;
}
t1 = t1->next;
t2 = t2->next;
}
else if (t1->expn > t2->expn) {
t->coef = t1->coef;
t->expn = t1->expn;
l->next = t;
l = t;
t1 = t1->next;
}
else {
t->coef =t2->coef;
t->expn = t2->expn;
l->next = t;
l = t;
t2 = t2->next;
}
}
if (t1) l->next = t1;
if (t2) l->next = t2;
}
void MulltiPolyn(PolyList& LC, PolyList LA, PolyList LB)//多项式相乘
{
PolyList l, t, t1, t2,pre,temp;
LC = new PNode;
LC->next = NULL;
l = LC;
t1 = LA->next;
t2 = LB->next;
while (t1) {//让每一个LB中的数据都与LA相乘
t2 = LB->next;//每次从头遍历
while (t2) {
t = new PNode;
t->coef = t2->coef*t1->coef;
t->expn = t2->expn+t1->expn;
pre = LC;//利用前驱,判断插入位置
while (pre->next && pre->next->expn > t->expn) {//找位置
pre = pre->next;
}
if (pre->next == NULL || pre->next->expn < t->expn) {//指数不相同,插入
t->next = pre->next;
pre->next = t;
}
else {//指数相同,相加
pre->next->coef += t->coef;
if(pre->next->coef==0){
temp=pre->next;
pre->next=temp->next;
delete temp;
}
}
t2 = t2->next;
}
t1 = t1->next;
}
}
2.1 两个有序序列的中位数
2.1.1 解题思路及伪代码

2.1.2 总结解题所用的知识点
- 顺序表的结构体定义
- 建立顺序表
- 顺序表的合并
2.2 一元多项式的乘法与加法运算
2.2.1 解题思路及伪代码
同类型合并的过程中可能会产生系数为0的项,这时候必须删除这一项。删除掉节点后记得释放掉这块空间,否则导致内存泄漏。
2.2.2 总结解题所用的知识点
- 链表结构体的构建
- 建立链表
- 链表的合并
- 尾插法
- 链表的前驱和后继
3.阅读代码(1分)
找1份优秀代码,理解代码功能,并讲出你所选代码优点及可以学习地方。主要找以下类型代码:
考研题种关于线性表内容。可以找参加过考研的学长学姐拿。尤其是想要考研同学,可以结合本章内容,用考研题训练学习。
ACM题解
leecode面试刷题网站,找线性表相关题目阅读分析。eecode经典题目
注意:不能选教师布置在PTA的题目。完成内容如下。
3.1 题目及解题代码
可截图,或复制代码,需要用代码符号渲染。
题目(来源:力扣(LeetCode))
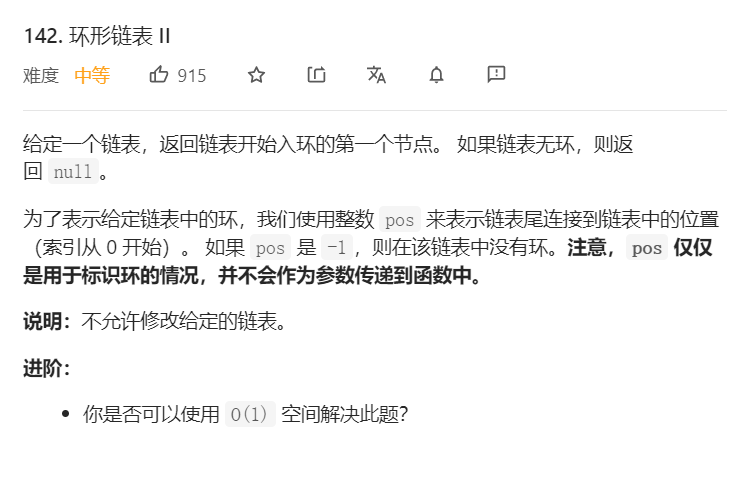
样例:
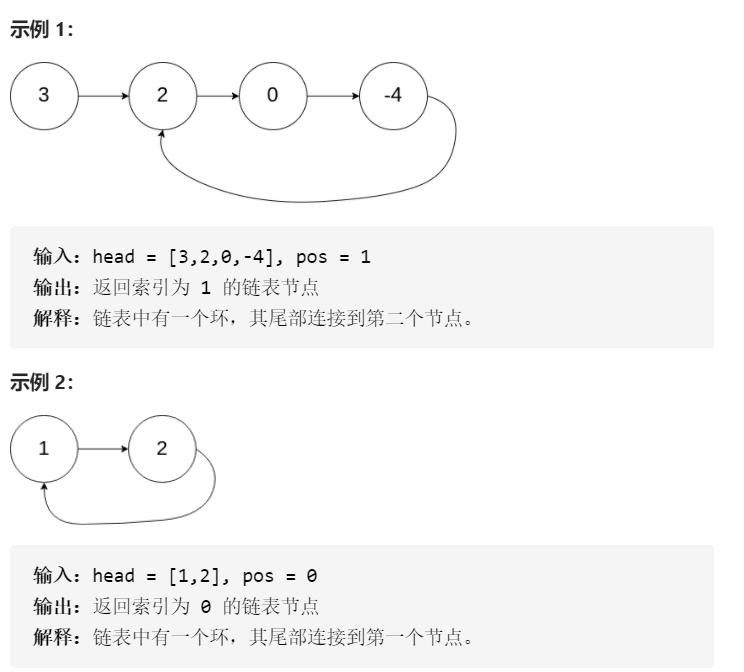

3.2 该题的设计思路及伪代码
链表题目,请用图形方式展示解决方法。同时分析该题的算法时间复杂度和空间复杂度。
思路与算法
我们使用两个指针,fast 与 slow。它们起始都位于链表的头部。随后,slow 指针每次向后移动一个位置,而fast 指针向后移动两个位置。如果链表中存在环,则 fast 指针最终将再次与slow 指针在环中相遇。
如下图所示,设链表中环外部分的长度为 a。slow 指针进入环后,又走了 b 的距离与fast 相遇。此时,fast 指针已经走完了环的 n圈,因此它走过的总距离为 a+n(b+c)+b=a+(n+1)b+nc。
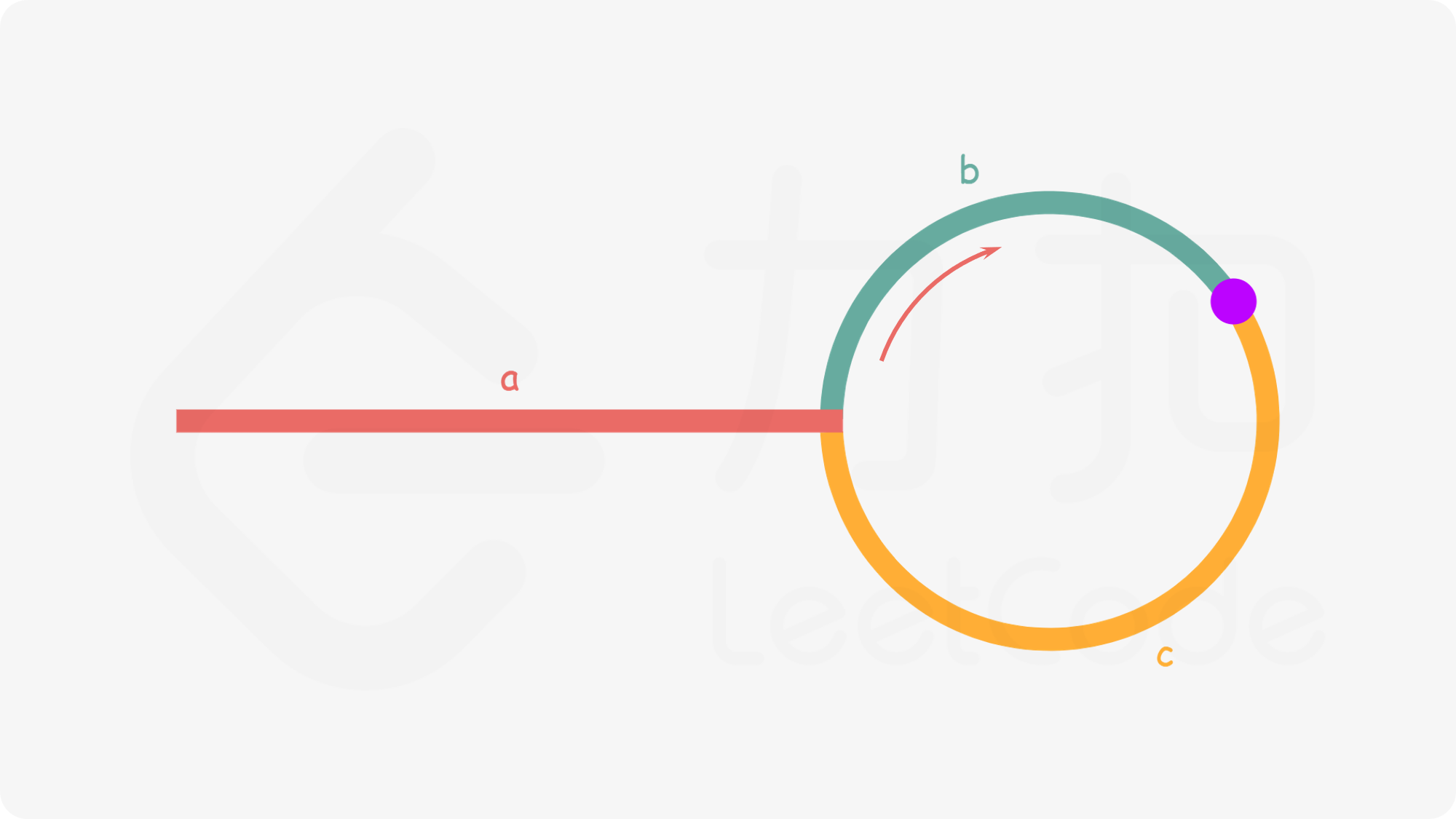
根据题意,任意时刻,fast 指针走过的距离都为slow 指针的 22 倍。因此,我们有
a+(n+1)b+nc=2(a+b)⟹a=c+(n−1)(b+c)
有了 a=c+(n-1)(b+c)a=c+(n−1)(b+c) 的等量关系,我们会发现:从相遇点到入环点的距离加上 n-1 圈的环长,恰好等于从链表头部到入环点的距离。
因此,当发现slow 与fast 相遇时,我们再额外使用一个指针ptr。起始,它指向链表头部;随后,它和slow 每次向后移动一个位置。最终,它们会在入环点相遇。
代码(https://leetcode-cn.com/problems/linked-list-cycle-ii/solution/huan-xing-lian-biao-ii-by-leetcode-solution/)
struct ListNode* detectCycle(struct ListNode* head) {
struct ListNode *slow = head, *fast = head;
while (fast != NULL) {
slow = slow->next;
if (fast->next == NULL) {
return NULL;
}
fast = fast->next->next;
if (fast == slow) {
struct ListNode* ptr = head;
while (ptr != slow) {
ptr = ptr->next;
slow = slow->next;
}
return ptr;
}
}
return NULL;
}
复杂度分析
- 时间复杂度:O(n)在最初判断快慢指针是否相遇时,slow 指针走过的距离不会超过链表的总长度;随后寻找入环点时,走过的距离也不会超过链表的总长度。所以时间复杂度为O(n)。
- 空间复杂度:O(1)只使用了slow,fast,ptr 三个指针。
3.3 分析该题目解题优势及难点。
- 解题优势:双指针从同一个结点出发,利用二者速度差来间接算出链表头部到入环点的距离。
- 难点:此题对数学逻辑要求较高,需要先推出相关路径关系才能写出代码。