HDU-3038 How Many Answers Are Wrong

看半天题意没看懂，翻译也理解不懂，实在不知道该怎么写，数据看着也没什么关系，看完学长的分析才明白这题让干啥，不过最后还是借学长代码理解着才写出来，思路太拐了，不仔细想真不容易写。

并查集的比较典型的题吧。

仔细观察可以发现既然要判断矛盾就肯定知道与以前的数据有冲突的地方，因为没有说这个数列是不是正整数所以冲突的方式只有一种，比如先说了连个区间

1-10 10

1-5 2

6-10 5

跟明显第三句话就可以看出来问题了，第二个加第三个跟第一个不相等，但是他们表述的区间都是相同的，所以产生矛盾，不过这种矛盾应该怎么判断呢，我们可以以它的端点为点建立一个集合，他们的根就是能到达的最左端，如果都有相同的最左端那么就可以判断一下是否有矛盾产生。

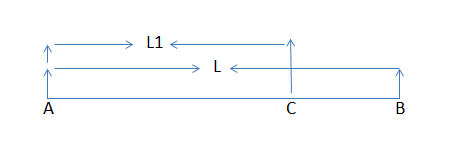
比如上面这个图, 我们已经知道了AB的长度和AC的长度，如果下面再来一个CB，我们就可以知道C的最左端是A，B的最左端也是A，那么就可以判断一个AC+CB的长度是不是等于AB的长度就可以了。。。。

如果最左端不相同的话合并的时候要先比较一下最左端是哪个

代码及详细解释如下：

#include<stdio.h>
#include<cstdio>
#include<cstring>
#include<string.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
#include<map>
#include<ctype.h>
#include<queue>
#include<stack>
#include<algorithm>
using namespace std;


const int maxn  = 200005;

int f[maxn], val[maxn];//Val存储最左端节点的最终数值

int Find(int x)
{
    int k = f[x];

    if(f[x] != x)
    {
        f[x] = Find(f[x]);//合并
        val[x] += val[k];//节点改变，值也要加起来
    }

    return f[x];
}

int main()
{
    int N, M;

    while(scanf("%d%d", &N, &M) != EOF)
    {
        int i, u, v, w, ans=0;

        for(i=0; i<=N; i++)
        {
            f[i] = i;
            val[i] = 0;
        }

        while(M--)
        {
            scanf("%d%d%d", &u, &v, &w);
            u = u-1;
            
            int ru = Find(u), rv = Find(v);//记录所给的左右端点
           
            if(ru == rv && val[u]+w != val[v])//判断所给两个端点最左的点是否相等，若想等再看数值是否相差W，不满足则表示是错误答案（看上边的解释样例，多想想就明白了）
                ans++;
            else if(ru < rv)//把最左的，也就是最小的作为节点
            {
                f[rv] = ru;
                val[rv] = val[u] - val[v] + w;
            }
            else if(ru > rv)//同理
            {
                f[ru] = rv;
                val[ru] = val[v] - val[u] - w;
            }
        }

        printf("%d
", ans);
    }

    return 0;
}