欢迎探讨,如有错误敬请指正
如需转载,请注明出处 http://www.cnblogs.com/nullzx/
1. 优先队列与索引优先队列
优先队列的原理大家应该比较熟悉,本质上就是利用完全二叉树的结构实现以log2n的时间复杂度删除队列中的最小对象(这里以小堆顶为例)。完全二叉树又可以通过数组下标实现索引,当插入一个对象的时候,利用上浮操作更新最小对象。当删除堆顶最小对象时,将末尾的对象放置到堆顶上,然后执行下沉操作。
优先队列有一个缺点,就是不能直接访问已存在于优先队列中的对象,并更新它们。这个问题在Dijistra算法中就有明显的体现,有时候我们需要更新已在队列中的顶点的距离。为此就需要设计一种新型的数据结构来解决这个问题,这就是本文要介绍的索引优先队列。
索引优先队用一个整数和对象进行关联,当我们需要跟新该对象的值时,可以通这个整数进行快速索引,然后对对象的值进行更新。当然更新后的对象在优先队列中的位置可能发生变化,这样以保证整个队列还是一个优先队列。
简易版的索引优先队列API
|
IndexPriorityQueue<T> |
|
|
IndexPriorityQueue(int capacity, Comparator<T> cmp) |
构造函数,capacity表示队列容量,cmp表示对象的比较器 |
|
void enqueue(int k, T t) |
将整数k和对象t进行关联,如果已有和k关联的对象,则将其更新为t |
|
int dequeue() |
出列,即删除最对象素并返回与它相关的整数。 |
|
void change(int k, T t) |
将和整数k和关联的对象更新为t |
注意与对象关联的整数k不能超过队列的容量。
2. 索引优先队列的实现原理
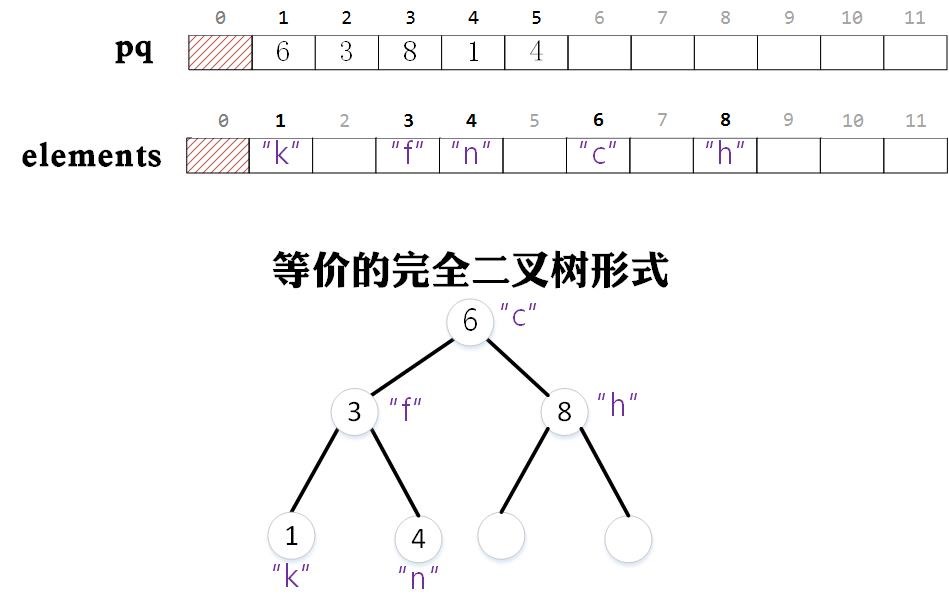
为了实现快速索引,我们首先尝试一个简单版本。我们创建两个数组分别是pq,elements。elements的作用是存储对象的引用,我们将每个对象存储在与之相关的整数作为下标的位置中,elements存储的对象不一定在数组中连续存放。pq存储是与对象相关的整数值,注意数组pq是连续存放的。此时pq作为优先队列,但是在上浮和下沉操作中,我们比较的是pq中值作为下标的elements数组中的值。这样我们就可以实现快速索引。
下图中,我们以字符串作为存储的对象类型,建立一个索引优先队列
从中我们可以看出,我们设计数组pq数组的目的。我们只需要对pq中的数值进行维护就可以实现一个优先队列,而elements中的对象的位置保持不变(出列时会置为null),这样就可以方便我们快速索引。比如通过elements数组我们可以知道与整数3相关的字符串为“f”。
在图中,我们插入一个与整数10相关的字符串“b”后,pq和elements中的值如下图所示。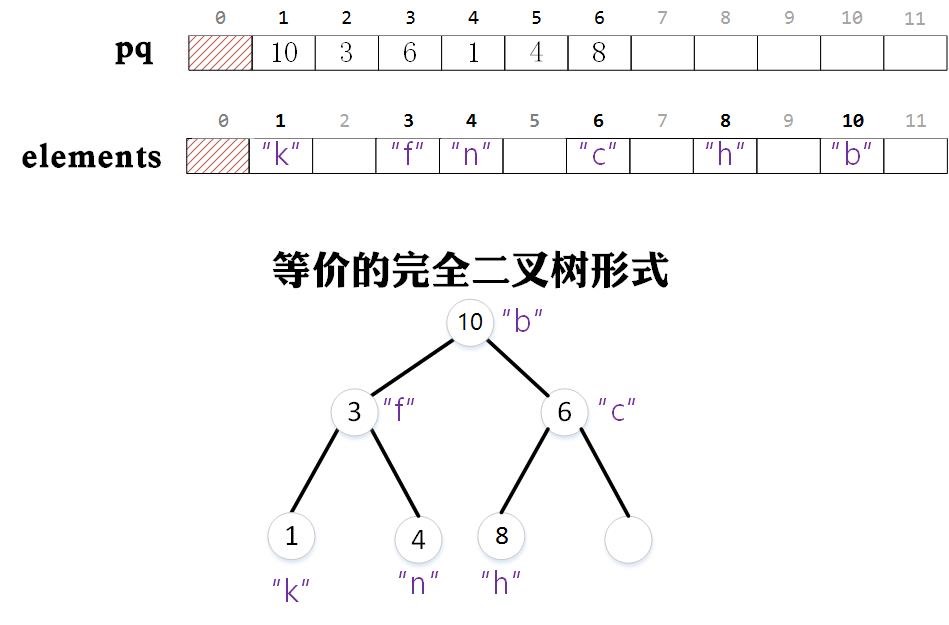
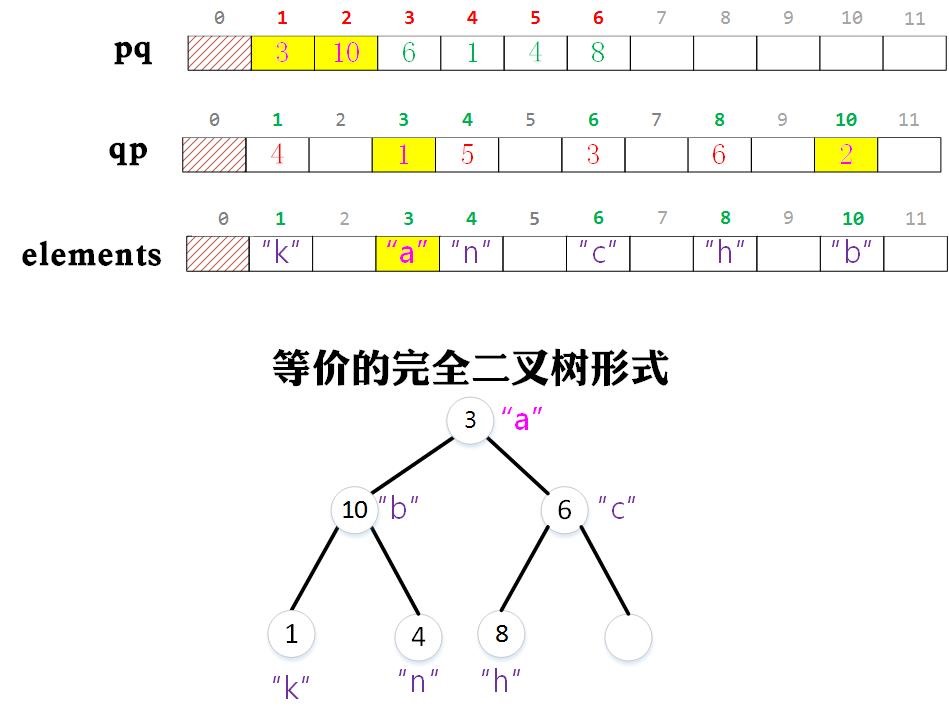
假设在上图的基础上,我们要将与整数3相关的字符串修改为“a”,那么我们只需要让elements[3] = “a”即可。然后去维护pq中的值。但是在维护pq中的值时出现了一个问题,我们不知道pq中哪个位置中的值为3,只能从都到尾遍历,找到这个元素所在的位置后进行上浮和下沉操作(因为我们必须通过下标才能快速找到父节点或者孩子节点)。为了能够快速找到pq中元素值对应的下标,我们需要额外设置一个数组qp,它的作用是存储与对象相关的整数在pq数组中的下标,并在上浮和下沉的过程中同时维护它。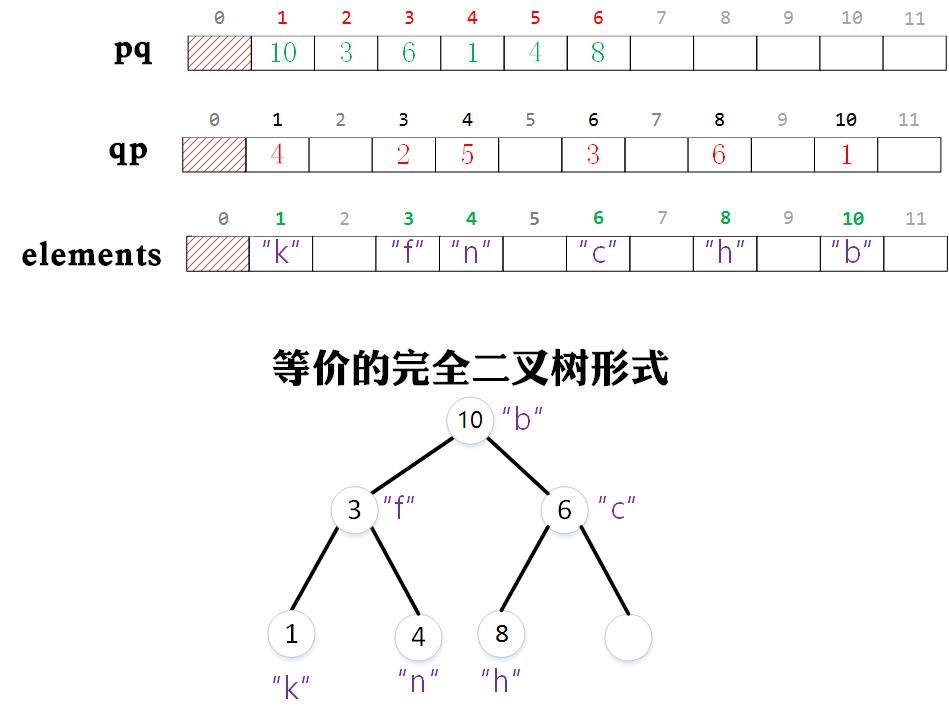
在上述的基础上,假设我们需要将与整数3相关的字符串修改为“a”,那么我们只需要让elements[3] = “a”,然后通过qp[3]中的值2就可以知道数组pq中值为3的下标为2,然后对pq[2]进行上浮或下沉操作。这里显然需要进行上浮操作,那么我们要交换pq[1]和pq[2]的值。这个时候我们需要注意的是,在交换pq数组中的两个元素的值时,我们也需要交换qp对应两个元素的值,因为与对象相关的整数在pq的不同位置上,那么显然该整数在pq所在的下标也变了,所以qp中的值也应该发生变化。而需要交换的qp中的两元素的下标正好就是pq中两元素的值。结果如下图所示。所以我们也需要交换qp[3]和qp[10]的值。
3. 索引优先队列的代码实现
上述的索引优先队列的原理中不能将数字0与对象进行关联,因为三个数组没有使用下标为0的位置。如果要实现与数字0进行关联,入列时只需要每个关联的数字加1;当出列时,我们只需要将返回的数字减1。
package datastruct;
import java.util.Arrays;
import java.util.Comparator;
public class IndexPriorityQueue<T> {
private int[] pq;
private int[] qp;
private Object[] element;
private final int capacity;
private int size;
private Comparator<? super T> cmp;
private static class Cmp<T> implements Comparator<T>{
@SuppressWarnings({ "unchecked", "rawtypes" })
@Override
public int compare(T t1, T t2) {
return ((Comparable)(t1)).compareTo(t2);
}
}
private static void swap(int[] a, int i, int j){
int tmp;
tmp = a[i];
a[i] = a[j];
a[j] = tmp;
}
//与对象关联的整数范围是[0,capacity-1]
public IndexPriorityQueue(int capacity, Comparator<T> cmp){
this.capacity = capacity;
pq = new int[capacity+1];
qp = new int[capacity+1];
Arrays.fill(qp, -1);
element = new Object[capacity+1];
if(cmp == null){
this.cmp = new Cmp<T>();
}
}
public void enqueue(int k, T t){
k++;//使得关联的整数可以为0
if(k > capacity){
throw new IllegalArgumentException();
}
if(qp[k] != -1){
element[k] = t;
swim(qp[k]);
sink(qp[k]);
return;
}
size++;
pq[size] = k;
qp[k] = size;
element[k] = t;
swim(size);
}
@SuppressWarnings("unchecked")
private void swim(int child){
int parent = child/2;
while(parent > 0){
if(cmp.compare((T)element[pq[child]], (T)element[pq[parent]]) < 0){
swap(pq, child, parent);
swap(qp, pq[child], pq[parent]);
child = parent;
parent = child/2;
}else{
break;
}
}
}
public int dequeue(){
if(size == 0){
throw new IllegalArgumentException();
}
int r = pq[1];
element[r] = null;
swap(pq, size, 1);
swap(qp, pq[size], pq[1]);
pq[size] = -1;
size--;
sink(1);
r--;//使得关联的整数可以为0
return r;
}
@SuppressWarnings("unchecked")
private void sink(int parent){
int child = parent*2;
while(child <= size){
if(child + 1 <= size){
int r = cmp.compare((T)element[pq[child]], (T)element[pq[child+1]]);
child = r > 0 ? child+1 : child;
}
if(cmp.compare((T)element[pq[child]], (T)element[pq[parent]]) < 0){
swap(pq, parent, child);
swap(qp, pq[parent], pq[child]);
parent = child;
child = parent*2;
}else{
break;
}
}
}
public void change(int k, T t){
k++;
if(qp[k] == -1){
throw new IllegalArgumentException();
}
element[k] = t;
swim(qp[k]);
sink(qp[k]);
}
public int size(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
public static void main(String[] args){
IndexPriorityQueue<String> ipq = new IndexPriorityQueue<String>(11, null);
ipq.enqueue(0, "k");
ipq.enqueue(6, "d");
ipq.enqueue(3, "f");
ipq.enqueue(4, "c");
ipq.enqueue(0, "a");
while(!ipq.isEmpty()){
System.out.println(ipq.dequeue());
}
}
}
4. 参考内容
[1]. 算法(第4版)Robert Sedgewick 人民邮电出版社