一、连续数组求和
Leetcode 53 最大子序和
题目描述:给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6
说明:解释: 连续子数组 [4,-1,2,1] 的和最大,为6。
思路1:判断加了当前数之后,是否会使得和增大,如果不会,就判断当前的和是否比num这个数大,如果没有,则当前使和最大的数就是num这个数;如果会,就将其加入list中;如果当前的num加进去之后,使得和更低了,也将其加入list中,注意,这个list不是最终的list,为了得到最后的list,需要判断一下,当前得到的和是否比上一轮得到的和更大,如果没有,就不更新最终的list
思路1代码如下:
def maxSubArray(arr):
res_list = []
s = -2**31 #返回的和
ts =-2**31 #每轮连续最大和
Res_list = []
for num in arr:
if num > num + ts: #如果加了num后的结果比num一个值的时候还糟
res_list = [num]
ts = num
else: #如果加了num之后的结果能够使得和变大
res_list.append(num)
ts += num
if ts > s:#只有当前的和最大时,才输出
s = ts
Res_list = res_list
print(ts)
print(res_list)
return s,Res_list
思路2:分治法
先将数组一分为二,对每个子数组求连续子序列和最大值,再合并;
分为三种情况,左子序列(加mid);右子序列(不加mid);从mid开始向左延伸,得到延伸之后的包括mid的左子序列最大值+不加mid向右延伸,得到延伸之后的右子序列最大值
取这三种情况里面的最大值,就作为本轮得到的最大连续子序列和。
举个例子:
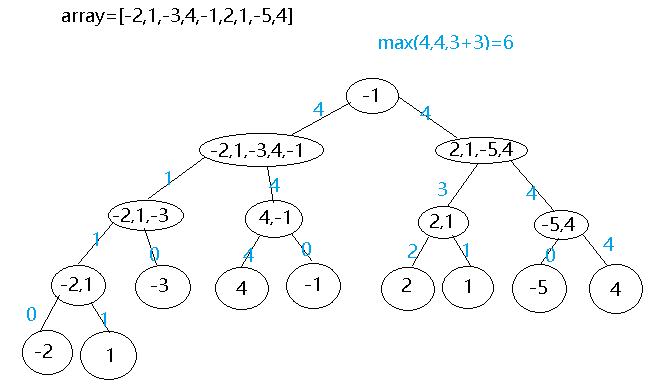
思路2代码如下:
def maxSubArray1(array,start,last): #举例 [-2,1,-3,4,-1]
mid = start + (last-start) // 2
if start == last: #递归的出口是只有一个数字的时候,如果该数字大于0,就保留该数字并返回;如果该数字小于0,就丢弃该数字,返回0
if array[start] > 0:
return array[start]
else:
return 0
'''
左[-2,1,-3] --> 左[-2,1] 右[-3]
右[4,-1]
'''
maxSumL = maxSubArray1(array,start,mid) #计算[start:mid]之间数的最长子序列和(包括mid)
maxSumR = maxSubArray1(array,mid+1,last) #计算[mid+1:last]之间数的最长子序列和(不包括mid)
'''因为上面的递归只计算了左半部分(包括mid),和右半部分分别的最长子序列和,那左边和右边加一起最大的最长子序列和是多少呢?
或者说右半部分加mid的子序列和会不会是最大呢?'''
maxsuml = 0
maxsumr = 0
temp_maxsum = 0
i = mid
while i >= start: #计算左半部分连同mid向左延伸最大和----从mid到start【逆序】,保留最大的连续和
temp_maxsum += array[i]
if temp_maxsum > maxsuml:
maxsuml = temp_maxsum
i -= 1
i = mid + 1
temp_maxsum = 0
while i <= last: #计算右半部分向右延伸最大的和,从mid+1到last【顺序】
temp_maxsum += array[i]
if temp_maxsum > maxsumr:
maxsumr = temp_maxsum
i += 1
maxSum = max(max(maxSumL,maxSumR),maxsuml+maxsumr)
return maxSum
array=[-2,1,-3,4,-1,2,1,-5,4]
start=0
last=len(array)-1
res = maxSubArray1(array,start,last)
print(res)
思路3:贪心法 时间复杂度O(N^2)
思路3代码如下:
def maxSubArray2(A):
if not A:
return 0
else:
subSum=maxSum=A[0]
for item in A[1:]:
subSum=max(item,item+subSum)
maxSum=max(subSum,maxSum)
return maxSum
Leetcode 560 和为K的子数组
题目描述:
给定一个整数数组和一个整数 k,你需要找到该数组中和为 k 的连续的子数组的个数。
示例:
输入:nums = [1,1,1], k = 2
输出: 2 , [1,1] 与 [1,1] 为两种不同的情况。
说明 :
- 数组的长度为 [1, 20,000]。
- 数组中元素的范围是 [-1000, 1000] ,且整数 k 的范围是 [-1e7, 1e7]。
Leetcode 523 连续的子数组和
题目描述:
给定一个包含非负数的数组和一个目标整数 k,编写一个函数来判断该数组是否含有连续的子数组,其大小至少为 2,总和为 k 的倍数,即总和为 n*k,其中 n 也是一个整数。
示例:
示例 1: 输入: [23,2,4,6,7], k = 6 输出: True 解释: [2,4] 是一个大小为 2 的子数组,并且和为 6 示例 2: 输入: [23,2,6,4,7], k = 6 输出: True 解释: [23,2,6,4,7]是大小为 5 的子数组,并且和为 42。
说明:
- 数组的长度不会超过10,000。
- 你可以认为所有数字总和在 32 位有符号整数范围内。