凸包

这可能（一定）是我上高中之前的最后一篇博文了！

今天闲的没事(其实我有一堆作业没写完)听膜你抄(点击进入)，莫名其妙看到了凸包，于是就在百度里输入了这俩字，于是看到了黄学长的文章，于是来到了博客园发了个这个玩意儿

正题：

1.什么是凸包？
（这里说平面凸包）凸包就是平面上有一些点，你要求出一个封闭图形使所有的点在这个封闭图形内，且这个图形的面积最小，且这个图形内的任意两点的连线不与封闭图形相交（我是这么理解的，说白了就是地上钉着一堆钉子，你有一个皮筋，要把这些钉子围起来，假设一开始皮筋是无限大的圆，所有钉子都在这里面，你一松手皮筋由于弹力开始收缩，最后皮筋会被钉子挡住（假设钉子无比坚硬），那么皮筋形成的图形就是凸包当我没说）
下面的图片来自维基百科，我们假设黑色的线是皮筋，毫无疑问松手之后他就变成了蓝色的线。蓝色的线就是这些点的凸包

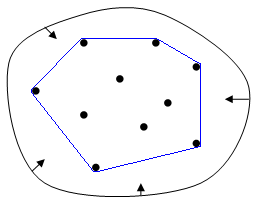
“在二维欧几里得空间中，凸包可想象为一条刚好包着所有点的橡皮圈。”——维基百科（强悍！一句话解释）

2.算法 （时间复杂度坠高的算法）（一种奇怪的方法）
i我们首先要建立坐标系（废话），每个点都有其坐标。（输入数据） O(n)
ii选取纵坐标最小的点，如果有多个点则选取横坐标最小的点。 O(n)
iii求出每个点与这个点的连线和x轴夹角的角度 O(n)
iiii按照角度由小到大排序  O(nlog₂n)//我们排序的目的是为了找连线与x轴夹角最小的点，所以只需遍历每个点更新即可，O(n)
iiiii找角度最小的点，把当前点和该点连线加入凸包 O(1)
iiiiii把上一步搜索到的最小的点当做当前的点，从步骤iii重复，直到求到ii找到的点为止。
时间复杂度O(nm)【m是凸包上点的个数，显然凸包上点越少越好】，最差O(n²)【所有点都在凸包上，重复n次】，最好O(n)【你说呢(滑稽)】

这种算法应该叫j什么什么s步进法，因为是依次找每个在凸包上的点。

代码 代更

3.g什么什么m扫描法(O(nlogn))

代更

然后呢这是洛谷板子题（USACO圈奶牛）的代码

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
using namespace std;
struct vesor
{
    double x,y,p;
    vesor(double x=0,double y=0):x(x),y(y){}
    friend vesor operator-(const vesor&a,const vesor&b){return vesor(a.x-b.x,a.y-b.y);}
    friend double operator^(const vesor&a,const vesor&b){return a.x*b.y-a.y*b.x;}
    double mod(){return sqrt(x*x+y*y);}
}a[10010];
bool youngsc(const vesor&a,const vesor&b){return a.p<b.p;}
bool vis[10010];
int s[10010],top;
int minj=1,n;
double ans;
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%lf%lf",&a[i].x,&a[i].y);
        if(a[minj].y>a[i].y||(a[minj].y==a[i].y&&a[minj].x>a[i].x))
        {
            minj=i;
        }
    }
    swap(a[1],a[minj]);
    for(int i=2;i<=n;i++)
    {
        a[i].x-=a[1].x;
        a[i].y-=a[1].y;
        a[i].p=atan2(a[i].y,a[i].x);
    }
    sort(a+2,a+1+n,[](const vesor&a,const vesor&b){return a.p<b.p;});//lambda表达式编译错误 版本
    a[1].x=0;
    a[1].y=0;
    for(int i=1;i<=n;i++)
    {
//        printf("%f %f %f
",a[i].x,a[i].y,a[i].p);
    }
    s[1]=1;
    s[2]=2;
    s[3]=3;
    top=3;
    for(int i=4;i<=n;i++)//while(前前->前)在(前->cur)的逆时针，那前死
    {
        while(top>2&&((a[s[top]]-a[s[top-1]])^(a[i]-a[s[top]]))<0)
            top--;
        s[++top]=i;
    }
    for(int i=1;i<top;i++)
    {
//        printf("%d %d
",s[i],s[i+1]);
        ans+=(a[s[i+1]]-a[s[i]]).mod();
    }
    ans+=(a[n]-a[1]).mod();
    printf("%.2f
",ans);
    return 0;
}