树有很多优美的性质,这题就是一个很好的例子.
在树上找出一条不超过给定长度的路径,使得所有点到这条路径的距离的最大值最小.
可以证明,这条路径必定在树的直径上.很像NOIP树网的核.
两遍BFS,求出直径后(可能不唯一,但只需一条足够),把直径上所有边的权记录下来,并在原图上把它们改成0,再一遍BFS,求出不是直径上的点离直径的最长距离S’.这样,我们可以二分答案,由于路径只为一条,所以对应到数组中是连续的一段,判断是否可行即可(这里可以用二分查找O(logn),我写了O(n)的朴素),设最小可能值为S.
1、若当S’>S,S’不可能增大,即那时那个不是直径上的点一定能覆盖到.
2、若当S’<S,S’增大后不会超过S.
可得出答案为Max(S,S’).
简单证明:
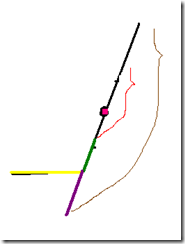
棕色是直径,粉色是中点,黄色是不是直径上的点离直径的最长路径,覆盖了红色部分,多出的一部分为绿色.
1、反证法.假设S’增大了.且S’(指原先的)>S,那么,紫色长度<黄色长度,那么黄+绿+黑就比直径还长了,自相矛盾.
2、假设S=绿+紫,因为直径的性质,所以紫>黄,所以S=绿+紫>绿+黄,即S>S’.S在另一边也易证.
var n,maxs,i,j,k,l,r,p,x,y,z,max,big,ans:longint;
e,b,w,first,last,dis,fa,fak,path,f,s,s2:array[0..600001] of longint;
procedure add(x,y,z:longint);
begin
inc(p);
e[p]:=y;w[p]:=z;
if first[x]=0 then first[x]:=p else b[last[x]]:=p;last[x]:=p;
end;
procedure BFS(start:longint;jilu:boolean);
var i,j,k:longint;
begin
filldword(dis,sizeof(dis) div 4,maxlongint);
i:=1;j:=1;f[1]:=start;fa[1]:=0;fak[1]:=0;dis[start]:=0;
repeat
k:=first[f[i]];
while k<>0 do
begin
if dis[f[i]]+w[k]<dis[e[k]] then
begin
dis[e[k]]:=dis[f[i]]+w[k];
j:=j+1;
f[j]:=e[k];
fa[j]:=i;
fak[j]:=k;
end;
k:=b[k];
end;
i:=i+1;
until i>j;
max:=-1;
for i:=1 to n do
if dis[i]>max then begin max:=dis[i];big:=i;end;
for i:=1 to n do
if f[i]=big then begin j:=i;break;end;
if jilu then
begin
path[0]:=0;
while fak[j]<>0 do
begin
inc(path[0]);
path[path[0]]:=fak[j];
j:=fa[j];
end;
end;
//for i:=1 to path[0] do write(w[path[i]],' ');writeln;
end;
function ok(x:longint):boolean;
var i,j,tot:longint;
begin
i:=0;while (i<=path[0])and(s[i]<=x) do i:=i+1;i:=i-1;
j:=path[0]+1;while (j>=1)and(s2[j]<=x) do j:=j-1;j:=j+1; ///二分???
if s[j-1]-s[i]<=maxs then exit(true) else exit(false);
end;
begin
assign(input,'mindist.in');
assign(output,'mindist.out');
reset(input);rewrite(output);
readln(n,maxs);
p:=0;
for i:=1 to n-1 do
begin
readln(x,y,z);
add(x,y,z);
add(y,x,z);
end;
BFS(1,true);
BFS(big,true);
s[0]:=0;for i:=1 to path[0] do s[i]:=s[i-1]+w[path[i]];
s2[path[0]+1]:=0;for i:=path[0] downto 1 do s2[i]:=s2[i+1]+w[path[i]];
for i:=1 to path[0] do
if odd(path[i]) then begin w[path[i]]:=0;w[path[i]+1]:=0;end
else begin w[path[i]]:=0;w[path[i]-1]:=0;end;
BFS(big,false);
l:=0;r:=300000000;
while l<r do
begin
if ok((l+r) div 2) then r:=(l+r) div 2
else l:=(l+r) div 2+1;
end;
if max>l then writeln(max)
else writeln(l);
close(input);close(output);
end.