$ color{#0066ff}{ 题目描述 }$
「Hanabi, hanabi……」
一听说祭典上没有烟火,Karen 一脸沮丧。
「有的哦…… 虽然比不上大型烟花就是了。」
还好 Shinobu 早有准备,Alice、Ayaya、Karen、Shinobu、Yoko 五人又能继续愉快地玩耍啦!
「噢……!不是有放上天的烟花嘛!」Karen 兴奋地喊道。
「啊等等……」Yoko 惊呼。Karen 手持点燃引信的烟花,「嗯??」
Yoko 最希望见到的是排列优美的烟火,当然不会放过这个机会…… 不过时间似乎已经不多了。
nn 个烟火排成一排,从左到右高度分别为 (h_1,h_2,cdots),这些高度两两不同。
每次 Yoko 可以选择两个相邻的烟火交换,这样的交换可以进行任意多次。
每次 Yoko 还可以选择两个不相邻的烟火交换,但这样的交换至多进行一次。
你的任务是帮助 Yoko 用最少次数的交换,使这些烟火从左到右的高度递增。
(color{#0066ff}{输入格式})
第一行包含一个正整数 (n)。
第二行包含 (n) 个正整数 (h_1,h_2,cdots),相邻整数之间用一个空格隔开。
(color{#0066ff}{输出格式})
输出一个整数,表示最少的交换次数。
(color{#0066ff}{输入样例})
5
3 5 4 1 2
(color{#0066ff}{输出样例})
5
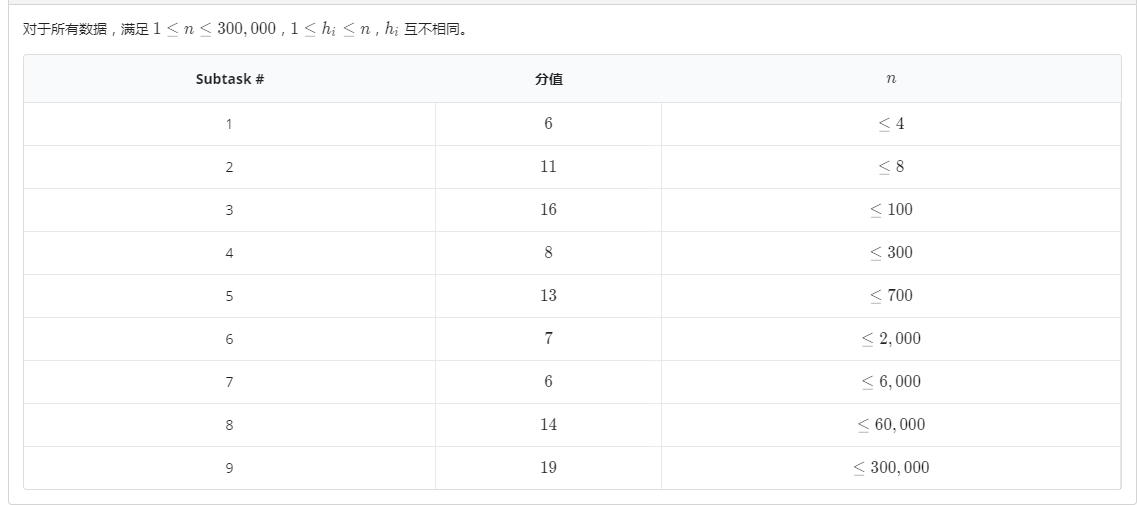
(color{#0066ff}{数据范围与提示})
一开始,(5) 个烟火的高度依次为 (3,5,4,1,2)。
第 (1) 次,交换第 (4) 根烟火和第 (5) 根烟火,交换后烟火的高度依次为 (3,5,4,2,1)。
第 (2) 次,交换第 (3) 根烟火和第 (4) 根烟火,交换后烟火的高度依次为 (3,5,2,4,1)。
第 (3) 次,交换第 (1) 根烟火和第 (2) 根烟火,交换后烟火的高度依次为 (5,3,2,4,1)。
第 (4) 次,交换第 (2) 根烟火和第 (3) 根烟火,交换后烟火的高度依次为 (5,2,3,4,1)。
第 (5) 次,交换第 (1) 根烟火和第 (5) 根烟火,交换后烟火的高度依次为 (1,2,3,4,5)。
可以证明这是交换次数最少的方案。
(color{#0066ff}{题解})
考虑没有交换任意两个数一次的操作,那么答案就是逆序对数
现在我们有一个交换任意两个数的操作
我们肯定是要让这次操作的贡献最大的
也就是说,减少的逆序对数最多
那么我们选的两个数,左面那个肯定是越靠左且越大为优,右面那个越靠右越小越优
也就是说,我们可能被交换的数就是所有前缀max取得的点和所有后缀min取得的点
然后我们处理出了这两个可能修改的位置数组,都是单调的
我们现在要在两个数组内分别选一个数,交换这两个数所对应的位置,使得对答案的贡献最大
对于一对([l,r]),交换它俩的贡献是([l,r]之间权值在[a[r],a[l]]之间的值的个数)
这就是二维数点了, 主席树可以维护
现在考虑怎么快速求出每个点的贡献
也就是说,对于每个可能的右端点,选一个最优的左端点
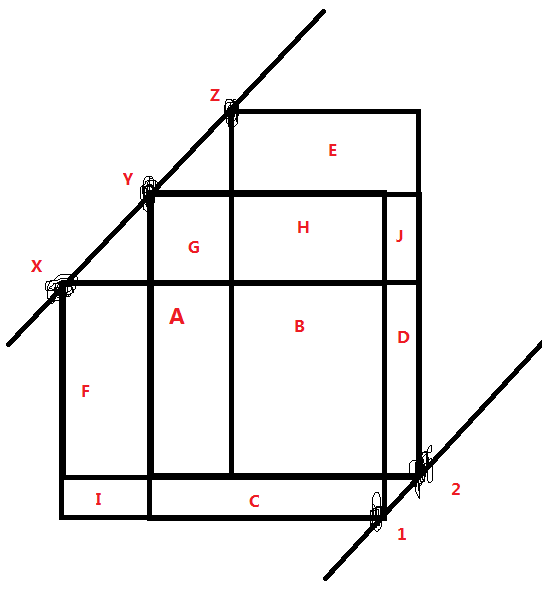
我们假设1选择y最优
那么可以得出(G+H>F+I)
然后对于2,因为(G+H+J>F)显然,所以y肯定比x有,也就是说最优点单调!!
于是我们就可以整体二分(O(nlog^2n))的求出右面每个点的贡献,然后取max,交换最优的l和r
最后树状数组求一下序列逆序对即可
#include<bits/stdc++.h>
#define LL long long
LL in() {
char ch; LL x = 0, f = 1;
while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
return x * f;
}
const int maxn = 3e5 + 10;
struct Tree {
protected:
int st[maxn];
int low(int x) { return x & (-x); }
int siz;
public:
void resize(int n) { siz = n; }
void add(int pos) { while(pos <= siz) st[pos]++, pos += low(pos); }
int query(int pos) { int re = 0; while(pos) re += st[pos], pos -= low(pos); return re; }
}s;
struct node {
node *ch[2];
int num;
node(int num = 0): num(num) { ch[0] = ch[1] = NULL; }
};
int n, a[maxn];
node *root[maxn];
int st1[maxn], st2[maxn], top1, top2, to[maxn], ans[maxn];
LL tot;
void init() {
root[0] = new node();
root[0]->ch[0] = root[0]->ch[1] = root[0];
}
void add(node *&o, node *lst, int l, int r, int p) {
o = new node(), *o = *lst, o->num++;
if(l == r) return;
int mid = (l + r) >> 1;
if(p <= mid) add(o->ch[0], lst->ch[0], l, mid, p);
else add(o->ch[1], lst->ch[1], mid + 1, r, p);
}
int getnum(node *x, node *y, int l, int r, int ql, int qr) {
if(x->num == y->num) return 0;
if(ql <= l && r <= qr) return y->num - x->num;
int mid = (l + r) >> 1;
int cnt = 0;
if(ql <= mid) cnt += getnum(x->ch[0], y->ch[0], l, mid, ql, qr);
if(qr > mid) cnt += getnum(x->ch[1], y->ch[1], mid + 1, r, ql, qr);
return cnt;
}
int getans(int l, int r) {
if(l >= r) return 0;
if(a[l] < a[r]) return 0;
return getnum(root[l - 1], root[r], 1, n, a[r] + 1, a[l] - 1);
}
void cdq(int l, int r, int a, int b) {
if(a > b) return;
if(l > r) return;
if(l == r) {
for(int i = a; i <= b; i++) {
int now = getans(st1[l], st2[i]);
if(now > ans[i]) ans[i] = now, to[i] = l;
}
return;
}
int mid = (a + b) >> 1;
//printf("now is work[%d, %d, %d, %d]
", l, r, a, b);
ans[mid] = 0;
for(int i = l; i <= r; i++) {
int now = getans(st1[i], st2[mid]);
if(now >= ans[mid]) ans[mid] = now, to[mid] = i;
}
cdq(l, to[mid], a, mid - 1);
cdq(to[mid], r, mid + 1, b);
}
void predoit() {
s.resize(n);
init();
for(int i = 1; i <= n; i++) add(root[i], root[i - 1], 1, n, a[i] = in());
//st1 can be left
//st2 can be right
for(int i = 1; i <= n; i++) {
while(top2 && a[i] < a[st2[top2]]) top2--;
if(a[i] > a[st1[top1]]) st1[++top1] = i;
st2[++top2] = i;
}
int max = 0, l = 0, r = 0;
cdq(1, top1, 1, top2);
for(int i = 1; i <= top2; i++)
if(max < ans[i]) max = ans[i], l = st1[to[i]], r = st2[i];
std::swap(a[l], a[r]);
if(l ^ r) tot++;
}
void getans() {
for(int i = n; i >= 1; i--) {
tot += s.query(a[i]);
s.add(a[i]);
}
printf("%lld
", tot);
}
int main() {
n = in();
predoit();
getans();
return 0;
}