P1959 遗址_NOI导刊2009普及（6）

题意：平面上n个点（坐标$0le x,yle 5000，n le 3000$） 

　　　求以其中四个点为顶点的正方形的最大面积

$O(n^2)$枚举两个点作为当前正方形的对角线

那么如何求出另外两个点呢？

设一个点为$（ax，ay）$，另一个为$（bx，by）$

所求点$（cx，cy），（dx，dy）$

考虑正方形中点$(frac{ax+bx}{2},frac{ay+by}{2})$

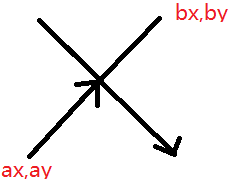
可以求出左边的向量为$(frac{bx-ax}{2},frac{by-ay}{2})$

右边的向量等于左边的向量旋转（自己举例推）$(frac{by-ay}{2},frac{ax-bx}{2})$

于是，右下角的点的坐标等于中点加右边的向量

　　　左上角点的坐标等于中点减右边的向量

如果那两个点是小数，是不成立的

怎么判断呢？

可以发现，那两个点的结果是由ax，ay，bx，by通过加加减减之后除以二得到的，

也就是说ax，ay，bx，by通过加加减减得到的应该是偶数

因此ax，ay，bx，by中必须要有偶数个奇数才成立！

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cctype>
#include<algorithm>
using namespace std;
#define olinr return
#define _ 0
#define love_nmr 0
#define DB double
inline int read()
{
    int x=0,f=1;
    char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-')
            f=-f;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    return x*f;
}
inline void put(int x)
{
    if(x<0)
    {
        x=-x;
        putchar('-');
    }
    if(x>9)
        put(x/10);
    putchar(x%10+'0');
}
int n;
struct node
{
    int x;
    int y;
}E[3050];
bool vis[5005][5005];
int ans;
double eps=1e-5;
inline int ok(int i,int j)
{
    int ax=E[i].x;
    int ay=E[i].y;
    int bx=E[j].x;
    int by=E[j].y;
    if((ax^ay^bx^by)&1) return -1;  //判断是否有奇数个奇数
    int cx=(ax+bx+by-ay)>>1;     //四个点的坐标
    int cy=(ay+by+ax-bx)>>1;
    int dx=(ax+bx-by+ay)>>1;
    int dy=(ay+by-ax+bx)>>1;
    if(cx<0||cy<0||dx<0||dy<0||cx>5000||cy>5000||dx>5000||dy>5000||!vis[cx][cy]||!vis[dx][dy]) return -1;  //没超范围并且点存在
    int fx=cx-ax;
    int fy=cy-ay;
    return fx*fx+fy*fy;   //面积
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
    {
        E[i].x=read();
        E[i].y=read();
        vis[E[i].x][E[i].y]=true;
    }
    for(int i=1;i<=n;i++)
        for(int j=1;j<=n;j++)
        {
            if(i==j) continue;
            ans=max(ans,ok(i,j));
        }
    put(ans);
    olinr ~~(0^_^0)+love_nmr;
}