作者:薛勤 | 微信公众号“ 代码艺术 ”作者
写在前面
本文是之前发表的文章《逐行解读HashMap源码》的下一篇,也是最后一篇。在《逐行解读HashMap源码》文章中,笔者主要分析了 HashMap 类的成员变量与成员方法,未涉及对 HashMap 中红黑树相关内容的分析。于是,笔者经过一段的时间的编写与打磨,写出了本文。本文主要内容包括对上一篇文章的些许补充以及对红黑树源码的详细解读。
如果读者没有阅读过上一篇内容,可以微信搜索公众号“代码艺术”搜索并阅读文章。
1. 红黑树概述
从本章节开始,笔者将对 HashMap 内部的 TreeNode 内部类源码开始分析,这部分的内容也就是我们所说的红黑树。
红黑树是建立在二叉查找树的基础之上的,二叉查找树又是建立在二叉树的基础之上。所以,我们需要从二叉树开始学习红黑树的发展脉络。
2. 二叉树
二叉树(英语:Binary tree)是每个节点最多只有两个分支(即不存在分支度大于2的节点)的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序,不能随意颠倒。
3. 二叉查找树
二叉查找树(英语:Binary Search Tree),也称为二叉搜索树、有序二叉树(ordered binary tree)或排序二叉树(sorted binary tree),是指一棵空树或者具有下列性质的二叉树:
- 若任意节点的左子树不空,则左子树上所有节点的值均小于它的根节点的值;
- 若任意节点的右子树不空,则右子树上所有节点的值均大于或等于它的根节点的值;
- 任意节点的左、右子树也分别为二叉查找树;
一颗二叉查找树如下图所示:

但是,当我们顺序插入一系列节点后,二叉查找树就退化为线性表,如下图所示:

虽然二叉查找树退化为线性表之后,最坏效率降为 O(n)。但依旧有很多改进版的二叉查找树可以使树高为O(log n),从而将最坏效率降至O(log n),如AVL树、红黑树等。
4. AVL树
AVL 树是最早被发明的自平衡二叉查找树。在AVL树中,任一节点对应的两棵子树的最大高度差为 1 ,因此它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是 O(logn)。增加和删除元素的操作则可能需要借由一次或多次树旋转,以实现树的重新平衡。
在 AVL 树中,节点的平衡因子是它的左子树的高度减去它的右子树的高度(有时相反)。带有平衡因子 1、0 或 -1 的节点被认为是平衡的。带有平衡因子 -2 或 2 的节点被认为是不平衡的,并需要重新平衡这个树。平衡因子可以直接存储在每个节点中,或从可能存储在节点中的子树高度计算出来。
AVL 树自平衡的方式是做一次或多次所谓的"AVL旋转"。
5. 红黑树
红黑树(英语:Red–black tree)也是一种自平衡二叉查找树。红黑树在二叉查找树的基础之上,对每个节点都增加了颜色属性,分为红色或黑色。在二叉查找树强制的一般要求以外,对于任何有效的红黑树增加了如下 5 条额外要求:
- 节点是红色或黑色。
- 根节点是黑色。
- 所有叶子都是黑色(叶子是NIL节点)。
- 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。
下面是一个具体的红黑树的图例:

红黑树的这些特性,保证了红黑树从根到叶子的最长的可能路径不多于最短的可能路径的两倍长,造成的结果是红黑树大致上是平衡的。如上图所示,"nil叶子"或"空(null)叶子"不包含数据而只充当树在此结束的指示。
对于红黑树的读与写,因为每一个红黑树都是一个(特殊的)二叉查找树,因此红黑树上的只读操作与普通二叉查找树上的只读操作相同。然而,在红黑树上进行插入操作和删除操作会导致不再符合红黑树的性质。恢复红黑树的性质需要少量 O(log n) 的颜色变更(实际是非常快速的)和不超过三次的树旋转(对于插入操作是两次)。虽然插入和删除很复杂,但操作时间仍可以保持为 O(log n) 次。
本章节开始结合 HashMap 源码讲解红黑树的插入、红黑树的删除、红黑树的自平衡、左旋、右旋等内容。
6. 链表转为红黑树的过程
HashMap 的桶类型除了 Node (链表)外,还有 TreeNode (树)。
TreeNode 类包含成员方法 treeify() ,该方法的作用是形成以当前 TreeNode 对象为根节点的红黑树。
树化过程不外乎是循环遍历链表,构造一颗二叉查找树,最后使用红黑树的平衡方法进行自平衡。
该方法源码如下:
final void treeify(Node<K,V>[] tab) {
TreeNode<K,V> root = null;
// 步骤①:循环遍历当前TreeNode链表
for (TreeNode<K,V> x = this, next; x != null; x = next) {
next = (TreeNode<K,V>)x.next;
x.left = x.right = null;
// 步骤②:如果还未设置根节点..
if (root == null) {
x.parent = null;
x.red = false;
root = x;
}
// 步骤③:如果已设置根节点..
else {
K k = x.key;
int h = x.hash;
Class<?> kc = null;
// 步骤④:从根节点开始遍历,插入新节点
for (TreeNode<K,V> p = root;;) {
int dir, ph;
K pk = p.key;
// 步骤⑤:比较当前节点的hash值与新节点的hash值
// 若是新节点hash值较小
if ((ph = p.hash) > h)
dir = -1;
// 若是新节点的hash值较大
else if (ph < h)
dir = 1;
// 若是新节点与当前节点的hash值相等
else if (
// 如果新节点的key没有实现Comparable接口..
(kc == null && (kc = comparableClassFor(k)) == null)
// 或者实现了Comparable接口但是k.compareTo(pk)结果为0
||(dir = compareComparables(kc, k, pk)) == 0)
// 则调用tieBreakOrder继续比较大小
dir = tieBreakOrder(k, pk);
TreeNode<K,V> xp = p;
// 步骤⑥:如果新节点经比较后小于等于当前节点且当前节点的左子节点为null,则插入新节点,反之亦然
if ((p = (dir <= 0) ? p.left : p.right) == null) {
x.parent = xp;
if (dir <= 0)
xp.left = x;
else
xp.right = x;
// 步骤⑦:平衡红黑树
root = balanceInsertion(root, x);
break;
}
}
}
}
// 步骤⑧:确保给定的根节点是所在桶的第一个节点
moveRootToFront(tab, root);
}
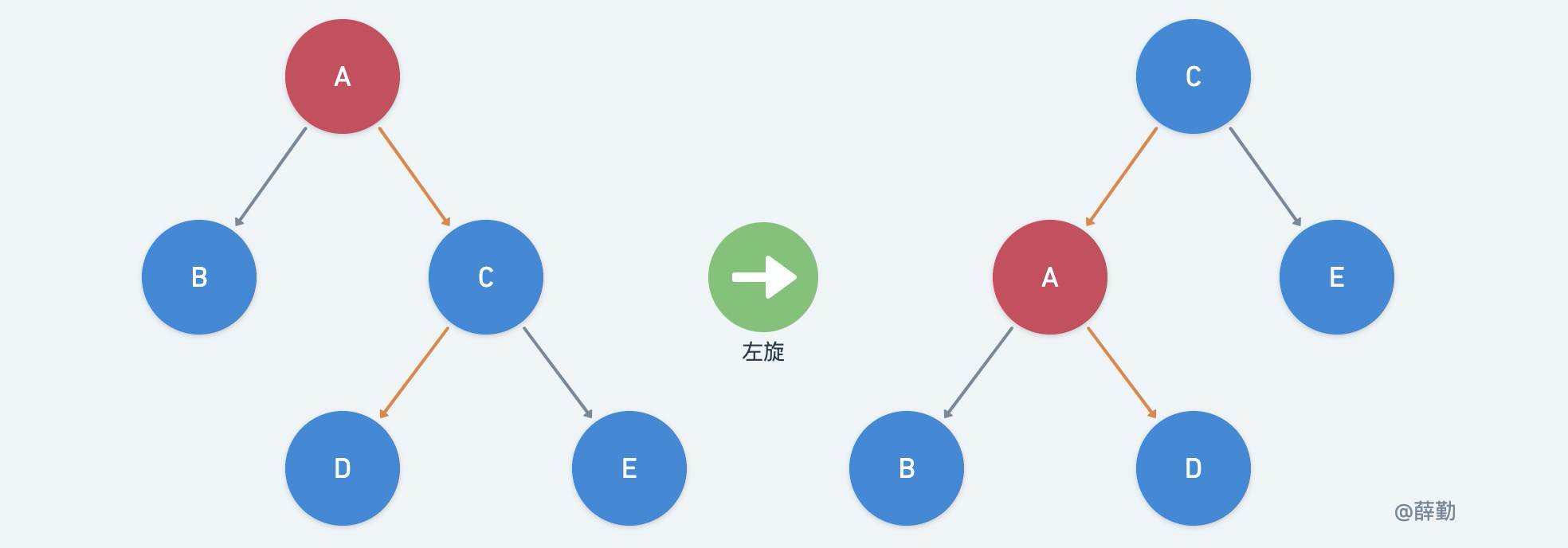
7. 红黑树的左旋和右旋
红黑树的左旋和右旋其实很简单,所谓的左旋是把要平衡的节点向左下旋转成一个叶子节点。
如下图所示:
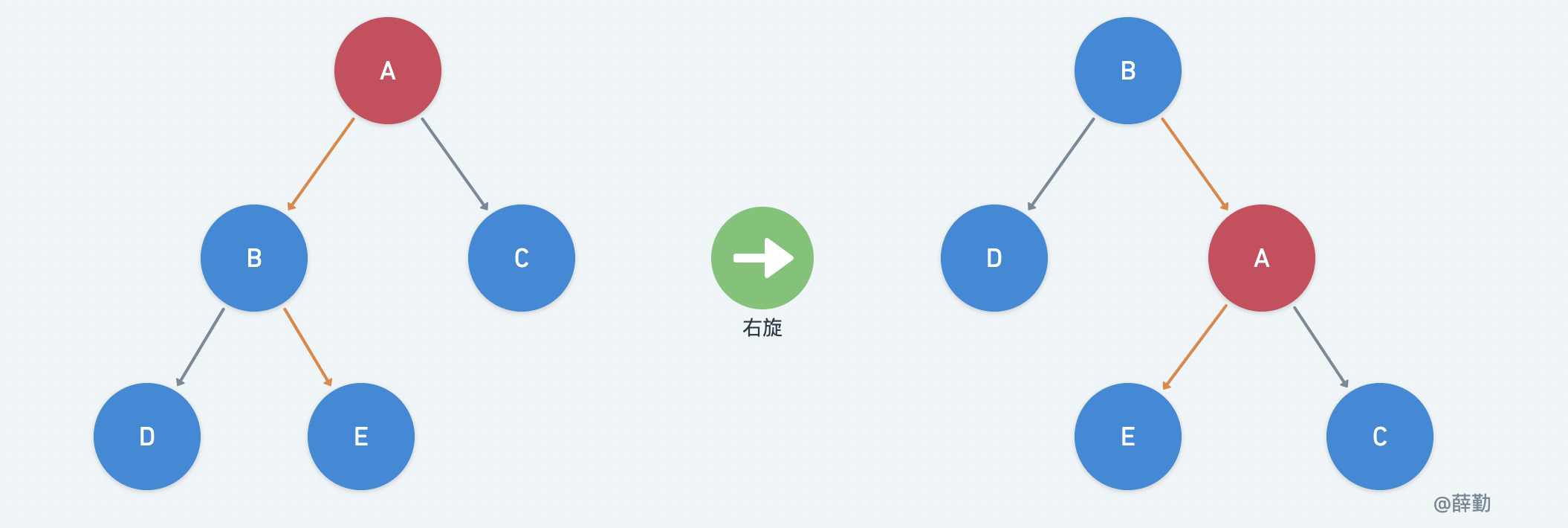
所谓的右旋是把要平衡的节点向右下旋转成一个叶子节点。
如下图所示:
在 HashMap 的源码中,左旋的实现代码如下:
static <K,V> TreeNode<K,V> rotateLeft(TreeNode<K,V> root,
TreeNode<K,V> p) {
// p: 当前节点
// r: 当前节点的右儿子
// rl: 当前节点的右儿子的左儿子
TreeNode<K,V> r, pp, rl;
// 如果当前节点和当前节点的右儿子不为空,就左旋
if (p != null && (r = p.right) != null) {
// 步骤①:当前节点的右儿子的左儿子成为当前节点的右儿子
if ((rl = p.right = r.left) != null)
rl.parent = p;
// 步骤②:当前节点的右儿子成为当前节点的父节点
if ((pp = r.parent = p.parent) == null)
// 如果当前节点是根节点,那么r的颜色必须是黑色
(root = r).red = false;
else if (pp.left == p)
pp.left = r;
else
pp.right = r;
r.left = p;
p.parent = r;
}
return root;
}
右旋的实现代码如下:
static <K,V> TreeNode<K,V> rotateRight(TreeNode<K,V> root,
TreeNode<K,V> p) {
// p: 当前节点
// l: 当前节点的左儿子
// lr: 当前节点的左儿子的右儿子
TreeNode<K,V> l, pp, lr;
// 如果当前节点和当前节点的左儿子不为空,就右旋
if (p != null && (l = p.left) != null) {
// 步骤①:当前节点的左儿子的右儿子成为当前节点的左儿子
if ((lr = p.left = l.right) != null)
lr.parent = p;
// 步骤②:当前节点的左儿子成为当前节点的父节点
if ((pp = l.parent = p.parent) == null)
// 如果当前节点是根节点,那么r的颜色必须是黑色
(root = l).red = false;
else if (pp.right == p)
pp.right = l;
else
pp.left = l;
l.right = p;
p.parent = l;
}
return root;
}
8. 红黑树的插入
红黑树是一棵特殊的二叉查找树,如同二叉查找树的插入一样,红黑树的插入,也需要判断插入节点与当前节点的大小。如果插入节点大于或等于当前节点,则插入当前节点的右子树;否则,插入到左子树。循环此过程,直到找到为空的叶子节点放入即可。
/**
* Tree version of putVal.
*/
final TreeNode<K,V> putTreeVal(HashMap<K,V> map, Node<K,V>[] tab,
int h, K k, V v) {
Class<?> kc = null;
boolean searched = false;
// root: 树根节点
TreeNode<K,V> root = (parent != null) ? root() : this;
for (TreeNode<K,V> p = root;;) {
// p: 当前节点
// dir: 标识新节点应该插入到当前节点的左子树还是右子树
// ph: 当前节点的hash值
// pk: 当前节点的key
int dir, ph; K pk;
// 步骤①:判断新节点应该插入到当前节点的左子树还是右子树
if ((ph = p.hash) > h)
dir = -1;
else if (ph < h)
dir = 1;
else if ((pk = p.key) == k || (k != null && k.equals(pk)))
return p;
else if ((kc == null &&
(kc = comparableClassFor(k)) == null) ||
(dir = compareComparables(kc, k, pk)) == 0) {
if (!searched) {
TreeNode<K,V> q, ch;
searched = true;
if (((ch = p.left) != null &&
(q = ch.find(h, k, kc)) != null) ||
((ch = p.right) != null &&
(q = ch.find(h, k, kc)) != null))
return q;
}
dir = tieBreakOrder(k, pk);
}
TreeNode<K,V> xp = p;
// 步骤②:终于从上向下遍历到了空的叶子节点,插入新节点
if ((p = (dir <= 0) ? p.left : p.right) == null) {
// 1.父节点指向新节点
Node<K,V> xpn = xp.next;
TreeNode<K,V> x = map.newTreeNode(h, k, v, xpn);
// 新节点位置在左子树还是右子树
if (dir <= 0)
xp.left = x;
else
xp.right = x;
xp.next = x;
// 2.新节点指向父节点
x.parent = x.prev = xp;
if (xpn != null)
// 如果有兄弟节点,兄弟节点的上一个节点指向新节点
((TreeNode<K,V>)xpn).prev = x;
// 最后平衡红黑树,并保证根节点在哈希桶的头部
moveRootToFront(tab, balanceInsertion(root, x));
return null;
}
}
}
红黑树的插入与二叉查找树的不同之处,在于最后的平衡部分。
插入节点之后的红黑树平衡方法如下:
/**
* 平衡红黑树-当新增后
* x: 影响平衡的点(俗称:当前节点)
*/
static <K,V> TreeNode<K,V> balanceInsertion(TreeNode<K,V> root,
TreeNode<K,V> x) {
// 新增节点x默认是红色
x.red = true;
// xp父节点 xpp祖父节点 xppl祖父左节点 xppr 祖父右节点(p: parent, l: left, r: right)
for (TreeNode<K,V> xp, xpp, xppl, xppr;;) {
if ((xp = x.parent) == null) {
// 步骤①:如果插入的是根节点,根据红黑树性质之根节点是黑色,直接涂黑即可
x.red = false;
return x;
}
// 步骤②:插入节点的父节点是黑色或者父节点是根节点,红黑树没有被破坏,不需要调整
else if (!xp.red || (xpp = xp.parent) == null)
return root;
// 父节点是祖父节点的左子节点
if (xp == (xppl = xpp.left)) {
// 步骤③:当前节点的父节点是红色,且叔叔节点也是红色
if ((xppr = xpp.right) != null && xppr.red) {
// 1.叔叔节点设置为黑色
xppr.red = false;
// 2.父节点设置为黑色
xp.red = false;
// 3.祖父节点设置为红色
xpp.red = true;
// 4.将当前节点指向祖父节点,从新的当前节点重新开始算法
x = xpp;
}
else {
// 步骤④:当前节点的父节点是红色,且叔叔节点是黑色,当前节点是其父右子节点
if (x == xp.right) {
// 当前节点的父节点作为新的当前节点,以新当节点为支点左旋
root = rotateLeft(root, x = xp);
// 重新赋值
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
// 父节点设置为黑色
xp.red = false;
if (xpp != null) {
// 祖父节点设置为红色
xpp.red = true;
// 以祖父节点为支点右旋
root = rotateRight(root, xpp);
}
}
}
}
// 父节点是祖父节点的右子节点
else {
// 步骤③:当前节点的父节点是红色,且叔叔节点也是红色
if (xppl != null && xppl.red) {
// 1.叔叔节点设置为黑色
xppl.red = false;
// 2.父节点设置为黑色
xp.red = false;
// 3.祖父节点设置为红色
xpp.red = true;
// 4.将当前节点指向祖父节点,从新的当前节点重新开始算法
x = xpp;
}
else {
// 步骤④:当前节点的父节点是红色,且叔叔节点是黑色,当前节点是其父左子节点
if (x == xp.left) {
// 当前节点的父节点作为新的当前节点,以新当节点为支点右旋
root = rotateRight(root, x = xp);
// 重新赋值
xpp = (xp = x.parent) == null ? null : xp.parent;
}
if (xp != null) {
// 父节点设置为黑色
xp.red = false;
if (xpp != null) {
// 祖父节点设置为红色
xpp.red = true;
// 以祖父节点为支点左旋
root = rotateLeft(root, xpp);
}
}
}
}
}
}
10. 红黑树的删除
红黑树的删除相比插入更加复杂,需要先从链表结构上进行删除,也就是处理当前节点的 next 指针与 prev 指针。如果当前树的节点太少,那么就将树退化为链表。然后,查找被删除节点的后继节点。所谓后继节点,就是当删除节点p后,如果p有子节点,p的子节点上移继承其位置。当找到后继节点,立即删除节点,如果被删除节点是红色,那么不需要平衡,否则平衡红黑树。
红黑树的删除方法代码如下:
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
boolean movable) {
int n;
if (tab == null || (n = tab.length) == 0)
// 不处理空的哈希表
return;
// 第 1 部分: 处理链表结构
// 通过被删除的key的哈希值查找桶(红黑树)的位置
int index = (n - 1) & hash;
// first、root: 红黑树的根节点
TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
// succ: 当前节点(被删除节点)的下一个节点
// pred: 当前节点(被删除节点)的上一个节点
TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
// 步骤①:从链表结构上删除当前节点(处理上一个节点的 next 指针与下一个节点的 prev 指针)
if (pred == null)
// 上一个节点为空,说明是要删除的是根节点,将红黑树的根节点索引改为当前节点的下一个节点
tab[index] = first = succ;
else
// 删除的不是根节点,就把当前节点的上一个节点的next指向当前节点的下一个节点
pred.next = succ;
if (succ != null)
// 当前节点的下一个节点不为空,就把下一个节点的prev指向当前节点的上一个节点
succ.prev = pred;
// 步骤②:删除节点完毕后,红黑树为空,直接返回
if (first == null)
return;
// 步骤③:更新root指针,并判断是否需要将树转为链表结构
if (root.parent != null)
root = root.root();
if (root == null || root.right == null ||
(rl = root.left) == null || rl.left == null) {
tab[index] = first.untreeify(map); // too small
return;
}
// 第 2 部分: 处理树结构
// p: 被删除的节点; replacement: 后继节点(删除节点p后,如果p有子节点,p的子节点上移继承其位置)
// pl: 被删除节点的左儿子; pr: 被删除节点的右儿子
TreeNode<K,V> p = this, pl = left, pr = right, replacement;
// 步骤①:查找被删除节点的后继节点,分以下几种情况
// ⑴ 被删除节点有左子树和右子树
if (pl != null && pr != null) {
TreeNode<K,V> s = pr, sl;
// 1.查找右子树最左叶子节点s与待删除节点p进行位置互换
while ((sl = s.left) != null) // find successor
s = sl;
// 2.交换最左叶子节点和待删除节点的颜色
boolean c = s.red; s.red = p.red; p.red = c; // swap colors
// sr:最左叶子节点的右儿子
TreeNode<K,V> sr = s.right;
// pp:被删除节点的父节点
TreeNode<K,V> pp = p.parent;
// 3.交换被删除节点p和最左叶子节点s的位置
// 判断最左叶子节点是否是被删除节点的右儿子(即右子树是否只有一个节点)分别处理节点s.right和p.parent的引用
if (s == pr) { // p was s's direct parent
p.parent = s;
s.right = p;
}
else {
TreeNode<K,V> sp = s.parent;
if ((p.parent = sp) != null) {
if (s == sp.left)
sp.left = p;
else
sp.right = p;
}
if ((s.right = pr) != null)
pr.parent = s;
}
p.left = null;
// 处理p.right和sr.parent的引用
if ((p.right = sr) != null)
sr.parent = p;
// 处理s.left和pl.parent的引用
if ((s.left = pl) != null)
pl.parent = s;
// 处理s.parent的引用和pp.left或pp.right
if ((s.parent = pp) == null)
root = s;
else if (p == pp.left)
pp.left = s;
else
pp.right = s;
// 4.交换最左叶子节点和被删除节点的位置完成
// 此时被删除节点p在原最左叶子节点的位置,现在被删除节点p没有左子树,如果有右子树,那么右儿子sr就是后继节点,否则后继节点指向自身
if (sr != null)
replacement = sr;
else
replacement = p;
}
// ⑵ 被删除节点只有左子树,后继节点就是左儿子
else if (pl != null)
replacement = pl;
// ⑶ 被删除节点只有右子树,后继节点就是右儿子
else if (pr != null)
replacement = pr;
// ⑷ 被删除节点没有子树,那么后继节点就指向自身
else
replacement = p;
// 步骤②:已经找到删除节点后的后继节点,这一步将从树中彻底删除节点p。
if (replacement != p) {
// 1.修改替代节点的父节点引用
TreeNode<K,V> pp = replacement.parent = p.parent;
// 2.将被删除节点的父节点对其的引用进行修改
if (pp == null)
root = replacement;
else if (p == pp.left)
pp.left = replacement;
else
pp.right = replacement;
// 3.彻底删除节点p
p.left = p.right = p.parent = null;
}
// 步骤③:删除节点完成,删除的是红色节点,不需要平衡;否则,平衡
TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);
// 步骤④:若没有后继节点,直接删除节点p
if (replacement == p) { // detach
TreeNode<K,V> pp = p.parent;
p.parent = null;
if (pp != null) {
if (p == pp.left)
pp.left = null;
else if (p == pp.right)
pp.right = null;
}
}
if (movable)
// 确保节点r是树根
moveRootToFront(tab, r);
}
删除红黑树节点之后的平衡代码如下,笔者认为,应当重点关注红黑树的变色、旋转逻辑。
/**
* 平衡红黑树-当删除后
* x: 影响平衡的点(俗称:当前节点)
*/
static <K,V> TreeNode<K,V> balanceDeletion(TreeNode<K,V> root,
TreeNode<K,V> x) {
// xp: 当前节点的父节点
// xpl: 当前节点的父节点的左儿子
// xpr: 当前节点的父节点的右儿子
for (TreeNode<K,V> xp, xpl, xpr;;) {
// 步骤①:当前节点是null或者是根节点,不改变红黑树的结构,不需要改变
if (x == null || x == root)
return root;
// 步骤②:当前节点成为根节点,置为黑色
else if ((xp = x.parent) == null) {
x.red = false;
return x;
}
// 步骤③:当前节点为红色,改为黑色后,不影响路径上黑色的数量,不需要改变
else if (x.red) {
x.red = false;
return root;
}
// 步骤④:当前节点为父节点的左儿子
else if ((xpl = xp.left) == x) {
// 如果兄弟节点是红色,那么父节点一定是黑色
if ((xpr = xp.right) != null && xpr.red) {
// 1.兄弟节点置为黑色
xpr.red = false;
// 2.父节点置为红色
xp.red = true;
// 3.以父节点为支点左旋
root = rotateLeft(root, xp);
// 4.刷新兄弟节点
xpr = (xp = x.parent) == null ? null : xp.right;
}
// 如果兄弟节点为空,将当前节点向上调整为父节点,继续循环
if (xpr == null)
x = xp;
else {
// sl: 兄弟节点的左儿子
// sr: 兄弟节点的右儿子
TreeNode<K,V> sl = xpr.left, sr = xpr.right;
if ((sr == null || !sr.red) &&
(sl == null || !sl.red)) {
// 如果兄弟节点没有红色孩子,则兄弟节点置为红色
xpr.red = true;
// 本轮结束,将当前节点向上调整为父节点,继续循环
x = xp;
}
else {
if (sr == null || !sr.red) {
// 如果兄弟节点的左儿子是红色就改为黑色
if (sl != null)
sl.red = false;
// 并将兄弟节点置为红色
xpr.red = true;
// 以兄弟节点为支点右旋
root = rotateRight(root, xpr);
// 刷新兄弟节点
xpr = (xp = x.parent) == null ?
null : xp.right;
}
if (xpr != null) {
// 将兄弟节点的颜色染成和父节点一样
xpr.red = (xp == null) ? false : xp.red;
// 将兄弟节点的右儿子染成黑色,防止出现两个红色节点相连
if ((sr = xpr.right) != null)
sr.red = false;
}
if (xp != null) {
// 父节点置为黑色,并对其左旋,这样就能保证被删除的节点所在的路径又多了一个黑色节点,从而达到恢复平衡的目的
xp.red = false;
root = rotateLeft(root, xp);
}
// 调整完毕,下一次循环直接退出
x = root;
}
}
}
// 步骤⑤:当前节点为父节点的右儿子,同上
else { // symmetric
if (xpl != null && xpl.red) {
xpl.red = false;
xp.red = true;
root = rotateRight(root, xp);
xpl = (xp = x.parent) == null ? null : xp.left;
}
if (xpl == null)
x = xp;
else {
TreeNode<K,V> sl = xpl.left, sr = xpl.right;
if ((sl == null || !sl.red) &&
(sr == null || !sr.red)) {
xpl.red = true;
x = xp;
}
else {
if (sl == null || !sl.red) {
if (sr != null)
sr.red = false;
xpl.red = true;
root = rotateLeft(root, xpl);
xpl = (xp = x.parent) == null ?
null : xp.left;
}
if (xpl != null) {
xpl.red = (xp == null) ? false : xp.red;
if ((sl = xpl.left) != null)
sl.red = false;
}
if (xp != null) {
xp.red = false;
root = rotateRight(root, xp);
}
x = root;
}
}
}
}
}
写在最后
这篇逐行解读 HashMap 源码的文章到此终于结束!笔者从开始写下此文的前半部分到现在,已经过了半年,期间由于功力不足、时间有限一直断断续续。不过所幸,笔者始终没有放弃,坚持要写出一篇高质量的解读 HashMap 源码的文章。但是,笔者虽已完成大部分核心源码的解读,但受限于自身功力浅薄,未能写的尽善尽美,本文仍旧存有许多遗憾之处。如果有读者想对本文进行补充的话,欢迎通过微信公众号“代码艺术”联系我!
学习资源
版权声明
【本文版权归微信公众号"代码艺术"(ID:onblog)所有,若是转载请务必保留本段原创声明,违者必究。若是文章有不足之处,欢迎关注微信公众号私信与我进行交流!】
