Graph Regularized Nonnegative Matrix Factorization for Data Representation
从几何角度来看, 数据通常是从嵌入在高维环境空间中的低维流形采样的。然后, 人们希望找到一个紧凑的表示, 它揭示了隐藏的语义, 同时尊重了内在的几何结构
所有这些算法都使用所谓的局部不变的想法 , 即附近的点很可能有类似的嵌入。研究表明, 利用几何结构, 考虑局部不变性, 可以显著提高学习性能。
受到启发 作者提出了GNMF 明确考虑了局部不变性。我们通过构造最近的邻域图来编码数据空间的几何信息.
下面是NMF 的公式 和两种迭代规则


局部几何结构
局部几何结构可以通过数据点散射上的最近邻图进行有效建模。考虑具有 n 个顶点的图形, 其中每个顶点对应于一个数据点。对于每个数据点 xj, 我们找到它的 p 最近的邻居, 并在 xj 和它的邻居之间放置边缘。在图形上定义权重矩阵 w 有许多选择。其中最常用的三种方法如下:
1 0-1 0-1 Weighting 2 Heat Kernel Weighting. 3. Dot-Product
这样低维结构可以表示
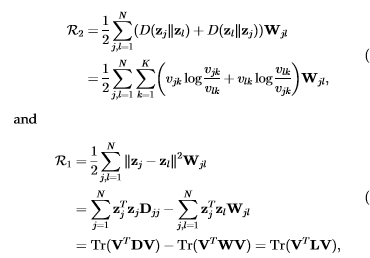
最后整个方程:
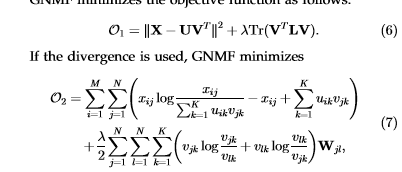
最后的迭代优化:Algorithms for Non-Negative Matrix Factorization,
先就写这些