网络战争
与01分数规划相结合
(dfrac{sum W_e}{|C|} < lambda) 对应 (sum(W_e - lambda) < 0)
二分 (lambda) 找到 (dfrac{sum W_e}{|C|}) 的最小值
(W_e - lambda le 0) 的边必选, 剩余的集合内的边一定不选,则边割集与流网络的割相对应, 求一个最小割即可
#include <bits/stdc++.h>
using namespace std;
const int N = 100 + 10;
const int M = (400 + 10) * 2;
const int INF = 1e9;
const double eps = 1e-8;
int n, m, S, T;
struct Edge
{
int to, nxt, w;
double flow;
}line[M];
int fist[N], idx;
int cur[N], d[N];
void add(int x, int y, int z)
{
line[idx] = {y, fist[x], z, 0};
fist[x] = idx ++;
line[idx] = {x, fist[y], z, 0};
fist[y] = idx ++;
}
bool bfs()
{
queue<int> q;
memset(d, -1, sizeof d);
q.push(S), d[S] = 0, cur[S] = fist[S];
while(!q.empty())
{
int u = q.front(); q.pop();
for(int i = fist[u]; i != -1; i = line[i].nxt)
{
int v = line[i].to;
if(d[v] == -1 && line[i].flow > 0)
{
d[v] = d[u] + 1;
cur[v] = fist[v];
if(v == T) return 1;
q.push(v);
}
}
}
return 0;
}
double find(int u, double limit)
{
if(u == T) return limit;
double flow = 0;
for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
{
cur[u] = i;
int v = line[i].to;
if(d[v] == d[u] + 1 && line[i].flow > 0)
{
double t = find(v, min(line[i].flow, limit - flow));
if(t <= 0) d[v] = -1;
line[i].flow -= t;
line[i ^ 1].flow += t;
flow += t;
}
}
return flow;
}
double dinic(double mid)
{
double res = 0;
for(int i = 0; i < idx; i += 2)
if(line[i].w <= mid)
{
res += line[i].w - mid;
line[i].flow = line[i ^ 1].flow = 0;
}
else line[i].flow = line[i ^ 1].flow = line[i].w - mid;
double r = 0, flow;
while(bfs()) while(flow = find(S, INF)) r += flow;
return res + r;
}
int main()
{
scanf("%d%d%d%d", &n, &m, &S, &T);
memset(fist, -1, sizeof fist);
for(int i = 1; i <= m; ++ i)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c);
}
double l = 0, r = 1e7;
while(r - l > eps)
{
double mid = (l + r) / 2;
if(dinic(mid) < 0) r = mid;
else l = mid;
}
printf("%.2lf
", r);
return 0;
}
最优标号
每一位之间互不影响, 拆成每一位处理
把集合分为两类,一类是当前位为 (0) 的点, 一类是当前位为 (1) 的点
集合内部的点异或值为 (0) ,这些边不会对答案有贡献, 集合间的边异或值为 (1), 对答案有贡献
为了最小化边的数量, 跑最小割即可
建立虚拟源点和汇点
- 从源点向当前位初始值为 (0) 的点连一条容量为 (+infty) 的边.(保证该点一定和 (s) 在一个集合)
- 从当前位初始值为 (1) 的点向汇点连一条容量为 (+infty) 的边.(保证该点一定和 (t) 在一个集合)
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
typedef long long LL;
const int N = 500 + 10;
const int M = (3000 + N) * 2;
const int INF = 1e9;
int n, m, k, S, T;
struct Edge
{
int to, nxt, flow;
}line[M];
int fist[N], idx;
int cur[N], d[N];
int p[N];
PII edges[3010];
void add(int x, int y, int z)
{
line[idx] = {y, fist[x], z};
fist[x] = idx ++;
line[idx] = {x, fist[y], z};
fist[y] = idx ++;
}
bool bfs()
{
queue<int> q;
memset(d, -1, sizeof d);
q.push(S), d[S] = 0, cur[S] = fist[S];
while(!q.empty())
{
int u = q.front(); q.pop();
for(int i = fist[u]; i != -1; i = line[i].nxt)
{
int v = line[i].to;
if(d[v] == -1 && line[i].flow)
{
d[v] = d[u] + 1;
cur[v] = fist[v];
if(v == T) return 1;
q.push(v);
}
}
}
return 0;
}
int find(int u, int limit)
{
if(u == T) return limit;
int flow = 0;
for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
{
cur[u] = i;
int v = line[i].to;
if(d[v] == d[u] + 1 && line[i].flow)
{
int t = find(v, min(line[i].flow, limit - flow));
if(!t) d[v] = -1;
line[i].flow -= t;
line[i ^ 1].flow += t;
flow += t;
}
}
return flow;
}
LL dinic(int k)
{
memset(fist, -1, sizeof fist);
idx = 0;
for(int i = 1; i <= m; ++ i)
{
int a = edges[i].x, b = edges[i].y;
add(a, b, 1);
}
for(int i = 1; i <= n; ++ i)
if(p[i] >= 0)
{
if(p[i] >> k & 1) add(i, T, INF);
else add(S, i, INF);
}
int res = 0, flow;
while(bfs()) while(flow = find(S, INF)) res += flow;
return res;
}
int main()
{
scanf("%d%d", &n, &m);
S = 0, T = n + 1;
memset(fist, -1, sizeof fist);
for(int i = 1; i <= m; ++ i) scanf("%d%d", &edges[i].x, &edges[i].y);
scanf("%d", &k);
memset(p, -1, sizeof p);
for(int i = 1; i <= n; ++ i)
{
int a, b;
scanf("%d%d", &a, &b);
p[a] = b;
}
LL res = 0;
for(int i = 0; i <= 30; ++ i) res += dinic(i) << i;
printf("%lld
", res);
return 0;
}
最大获利
最大权闭合图做法
中转站的权值设为负值, 用户群的权值设为正值, 从用户群向可以提供服务的中转站连边, 该问题转化为最大权闭合图
- 从源点向权值为正的点连一条容量为权值的边
- 从权值为负的点向汇点连一条容量为权值的绝对值的边
- 原图内部的边的容量设为 (+infty)
#include <bits/stdc++.h>
using namespace std;
const int N = 50000 + 5000 + 10;
const int M = (N + 50000 * 2) * 2;
const int INF = 1e9;
int n, m, S, T;
struct Edge
{
int to, nxt, flow;
}line[M];
int fist[N], idx;
int cur[N], d[N];
void add(int x, int y, int z)
{
line[idx] = {y, fist[x], z};
fist[x] = idx ++;
line[idx] = {x, fist[y], 0};
fist[y] = idx ++;
}
bool bfs()
{
queue<int> q;
memset(d, -1, sizeof d);
q.push(S), d[S] = 0, cur[S] = fist[S];
while(!q.empty())
{
int u = q.front(); q.pop();
for(int i = fist[u]; i != -1; i = line[i].nxt)
{
int v = line[i].to;
if(d[v] == -1 && line[i].flow)
{
d[v] = d[u] + 1;
cur[v] = fist[v];
if(v == T) return 1;
q.push(v);
}
}
}
return 0;
}
int find(int u, int limit)
{
if(u == T) return limit;
int flow = 0;
for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
{
cur[u] = i;
int v = line[i].to;
if(d[v] == d[u] + 1 && line[i].flow)
{
int t = find(v, min(line[i].flow, limit - flow));
if(!t) d[v] = -1;
line[i].flow -= t;
line[i ^ 1].flow += t;
flow += t;
}
}
return flow;
}
int dinic()
{
int res = 0, flow;
while(bfs()) while(flow = find(S, INF)) res += flow;
return res;
}
int main()
{
scanf("%d%d", &n, &m);
S = 0, T = n + m + 1;
memset(fist, -1, sizeof fist);
for(int i = 1; i <= n; ++ i)
{
int x;
scanf("%d", &x);
add(m + i, T, x);
}
int res = 0;
for(int i = 1; i <= m; ++ i)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
res += c;
add(S, i, c);
add(i, a + m, INF);
add(i, b + m, INF);
}
printf("%d
", res - dinic());
return 0;
}
最大密度子图做法
把用户群直接看做是一条边,转化成无向图,获益转化为边权, 建造费用的负值转化为点权
目的是使得 (|V''| + |E'|) 最大, 与点和边带权的最大密度子图最大化的值 (|E'| + |V''| - g * |V'|) 对应, 即在 $ g = 0$ 时最大
建图:
- 从源点向每个基站连一条容量为 (U) 的边
- 从每个基站向汇点连一条容量为 (2 * g - dv - 2 * pv + U) 的边
- 两个基站之间的双向边的容量设为边权
(c(S, T) = U * n + 2 * g * |V'| - 2 * |E'| - 2 * |V''| = U * n - 2 * |E'| - 2 * |V''|)
找到了最小割和 (|V''| + |E'|) 之间的关系, 求最小割即可使目标值最大化
#include <bits/stdc++.h>
using namespace std;
const int N = 5000 + 10;
const int M = (N * 2 + 50000 + 10) * 2;
const int INF = 1e9;
int n, m, S, T;
struct Edge
{
int to, nxt, flow;
}line[M];
int fist[N], idx;
int cur[N], d[N];
int dg[N], p[N];
void add(int x, int y, int z1, int z2)
{
line[idx] = {y, fist[x], z1};
fist[x] = idx ++;
line[idx] = {x, fist[y], z2};
fist[y] = idx ++;
}
bool bfs()
{
queue<int> q;
memset(d, -1, sizeof d);
q.push(S), d[S] = 0, cur[S] = fist[S];
while(!q.empty())
{
int u = q.front(); q.pop();
for(int i = fist[u]; i != -1; i = line[i].nxt)
{
int v = line[i].to;
if(d[v] == -1 && line[i].flow)
{
d[v] = d[u] + 1;
cur[v] = fist[v];
if(v == T) return 1;
q.push(v);
}
}
}
return 0;
}
int find(int u, int limit)
{
if(u == T) return limit;
int flow = 0;
for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
{
cur[u] = i;
int v = line[i].to;
if(d[v] == d[u] + 1 && line[i].flow)
{
int t = find(v, min(line[i].flow, limit - flow));
if(!t) d[v] = -1;
line[i].flow -= t;
line[i ^ 1].flow += t;
flow += t;
}
}
return flow;
}
int dinic()
{
int res = 0, flow;
while(bfs()) while(flow = find(S, INF)) res += flow;
return res;
}
int main()
{
scanf("%d%d", &n, &m);
S = 0, T = n + 1;
memset(fist, -1, sizeof fist);
for(int i = 1; i <= n; ++ i)
{
scanf("%d", &p[i]);
p[i] *= -1;
}
for(int i = 1; i <= m; ++ i)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
add(a, b, c, c);
dg[a] += c, dg[b] += c;
}
int U = 0;
for(int i = 1; i <= n; ++ i) U = max(U, 2 * p[i] + dg[i]);
for(int i = 1; i <= n; ++ i)
{
add(S, i, U, 0);
add(i, T, U - 2 * p[i] - dg[i], 0);
}
printf("%d
", (U * n - dinic()) / 2);
return 0;
}
生活的艰辛
最大密度子图
最大化 (dfrac{|E'|}{|V'|}),转化成判断最大化 (|E'| - g * |V'|) 与 (0) 的关系
建图:
- 从源点向所有点连一条容量为 (U) 的边
- 从所有点向汇点连一条容量为 (2 * g - dv + U) 的边
- 图中原有边的容量设为 (1)
(c(S, T) = U * n + 2 * g * |V'| - 2 * |E'|)
找到了割与 (|E'| - g * |V'|) 的关系, 求最小割即可
#include <bits/stdc++.h>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
const int N = 100 + 10;
const int M = (N * 2 + 1000 + 10) * 2;
const int INF = 1e9;
const double eps = 1e-8;
int n, m, S, T, U;
struct Edge
{
int to, nxt;
double flow;
}line[M];
int fist[N], idx;
int cur[N], d[N];
int dg[N];
PII p[M];
int ans;
bool st[N];
void add(int x, int y, double z1, double z2)
{
line[idx] = {y, fist[x], z1};
fist[x] = idx ++;
line[idx] = {x, fist[y], z2};
fist[y] = idx ++;
}
bool bfs()
{
queue<int> q;
memset(d, -1, sizeof d);
q.push(S), d[S] = 0, cur[S] = fist[S];
while(!q.empty())
{
int u = q.front(); q.pop();
for(int i = fist[u]; i != -1; i = line[i].nxt)
{
int v = line[i].to;
if(d[v] == -1 && line[i].flow > 0)
{
d[v] = d[u] + 1;
cur[v] = fist[v];
if(v == T) return 1;
q.push(v);
}
}
}
return 0;
}
double find(int u, double limit)
{
if(u == T) return limit;
double flow = 0;
for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
{
cur[u] = i;
int v = line[i].to;
if(d[v] == d[u] + 1 && line[i].flow > 0)
{
double t = find(v, min(line[i].flow, limit - flow));
if(t <= 0) d[v] = -1;
line[i].flow -= t;
line[i ^ 1].flow += t;
flow += t;
}
}
return flow;
}
double dinic(double g)
{
memset(fist, -1, sizeof fist);
idx = 0;
for(int i = 1; i <= m; ++ i)
add(p[i].x, p[i].y, 1, 1);
for(int i = 1; i <= n; ++ i)
{
add(S, i, U, 0);
add(i, T, U + g * 2 - dg[i], 0);
}
double res = 0, flow;
while(bfs()) while(flow = find(S, INF)) res += flow;
return res;
}
void dfs(int u)
{
st[u] = 1;
if(u != S) ans ++;
for(int i = fist[u]; i != -1; i = line[i].nxt)
{
int v = line[i].to;
if(!st[v] && line[i].flow > 0) dfs(v);
}
}
int main()
{
scanf("%d%d", &n, &m);
S = 0, T = n + 1;
for(int i = 1; i <= m; ++ i)
{
int a, b;
scanf("%d%d", &a, &b);
dg[a] ++, dg[b] ++;
p[i] = {a, b};
}
U = m;
double l = 0, r = m;
while(r - l > eps)
{
double mid = (r + l) / 2;
double t = dinic(mid);
if(U * n - t > 0) l = mid;
else r = mid;
}
dinic(l);
dfs(S);
if(!ans) puts("1
1");
else
{
printf("%d
", ans);
for(int i = 1; i <= n; ++ i)
if(st[i])
printf("%d
", i);
}
return 0;
}
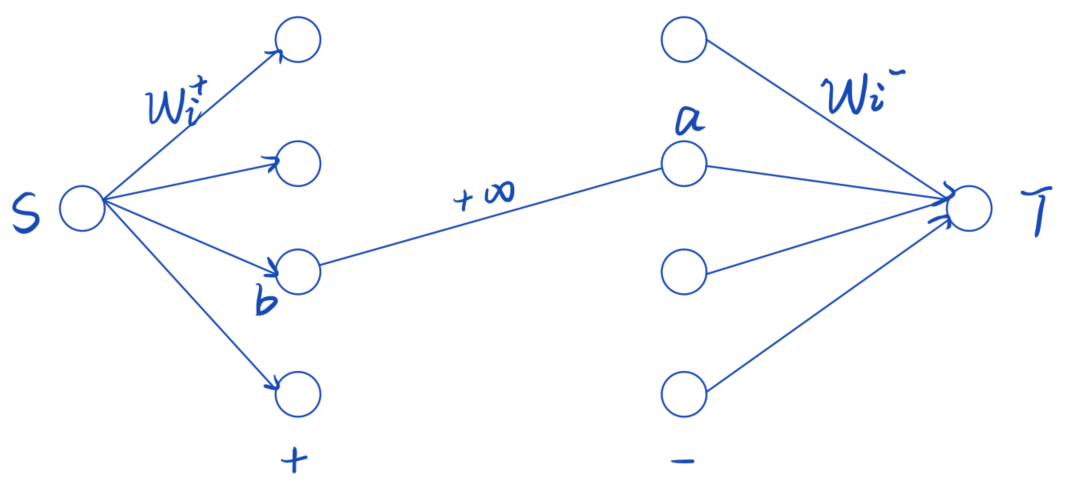
有向图破坏
最小点权覆盖集
如果有一条从 (a) 到 (b) 的边, 那么 (W_a^-) 和 (W_b^+) 必须选一个来删掉这条边
那么考虑把每个点拆点构造一个二分图, 第一排点都是作为出点的点, 第二排点都是作为入点的点
若有一条从 (a) 到 (b) 的边, 则从 (a^-) 向 (b^+) 连一条边无向边
则该问题转化为一个最小点权覆盖问题
- 从源点向入点连一条容量为 (W_i^+) 的边
- 从出点向汇点连一条容量为 (W_i^-) 的边
- 若有一条从 (a) 到 (b) 的边, 则从 (b^+) 向 (a^-) 连一条容量为 (+infty) 的边
最终找到割边输出方案
#include <bits/stdc++.h>
using namespace std;
const int N = 100 * 2 + 10;
const int M = (5000 + N + 10) * 2;
const int INF = 1e9;
int n, m, S, T;
struct Edge
{
int to, nxt, flow;
}line[M];
int fist[N], idx;
int cur[N], d[N];
bool st[N];
void add(int x, int y, int z)
{
line[idx] = {y, fist[x], z};
fist[x] = idx ++;
line[idx] = {x, fist[y], 0};
fist[y] = idx ++;
}
bool bfs()
{
queue<int> q;
memset(d, -1, sizeof d);
q.push(S), d[S] = 0, cur[S] = fist[S];
while(!q.empty())
{
int u = q.front(); q.pop();
for(int i = fist[u]; i != -1; i = line[i].nxt)
{
int v = line[i].to;
if(d[v] == -1 && line[i].flow)
{
d[v] = d[u] + 1;
cur[v] = fist[v];
if(v == T) return 1;
q.push(v);
}
}
}
return 0;
}
int find(int u, int limit)
{
if(u == T) return limit;
int flow = 0;
for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
{
cur[u] = i;
int v = line[i].to;
if(d[v] == d[u] + 1 && line[i].flow)
{
int t = find(v, min(line[i].flow, limit - flow));
if(!t) d[v] = -1;
line[i].flow -= t;
line[i ^ 1].flow += t;
flow += t;
}
}
return flow;
}
int dinic()
{
int res = 0, flow;
while(bfs()) while(flow = find(S, INF)) res += flow;
return res;
}
void dfs(int u)
{
st[u] = 1;
for(int i = fist[u]; i != -1; i = line[i].nxt)
{
int v = line[i].to;
if(!st[v] && line[i].flow) dfs(v);
}
}
int main()
{
scanf("%d%d", &n, &m);
S = 0, T = 2 * n + 1;
memset(fist, -1, sizeof fist);
for(int i = 1; i <= n; ++ i)
{
int w;
scanf("%d", &w);
add(S, i, w);
}
for(int i = 1; i <= n; ++ i)
{
int w;
scanf("%d", &w);
add(n + i, T, w);
}
for(int i = 1; i <= m; ++ i)
{
int a, b;
scanf("%d%d", &a, &b);
add(b, a + n, INF);
}
printf("%d
", dinic());
dfs(S);
int res = 0;
for(int i = 0; i < idx; i += 2)
{
int u = line[i ^ 1].to, v = line[i].to;
if(st[u] && !st[v]) res ++;
}
printf("%d
", res);
for(int i = 0; i < idx; i += 2)
{
int u = line[i ^ 1].to, v = line[i].to;
if(st[u] && !st[v])
{
if(u == S) printf("%d +
", v);
if(v == T) printf("%d -
", u - n);
}
}
return 0;
}
王者之剑
最大点权独立集
- 只能在偶数秒拿宝石
- 不可能同时拿走相邻格子上的宝石,把格子看成点,相邻格子之间连一条边,将格子黑白染色,可以形成一个二分图,则我们选择的格子一定是二分图上的独立集
- 两行两行走,对于任何一个独立集,可以构造出一种合法方案
故所有合法方案等价于二分图的一个独立集, 求一个最大点权独立集即可
#include <bits/stdc++.h>
using namespace std;
const int N = 10000 + 10;
const int M = (N + 5000 * 4 + 10) * 2;
const int INF = 1e9;
const int dx[] = {-1, 1, 0, 0};
const int dy[] = {0, 0, -1, 1};
int n, m, S, T;
struct Edge
{
int to, nxt, flow;
}line[M];
int fist[N], idx;
int cur[N], d[N];
int get(int x, int y)
{
return (x - 1) * m + y;
}
void add(int x, int y, int z)
{
line[idx] = {y, fist[x], z};
fist[x] = idx ++;
line[idx] = {x, fist[y], 0};
fist[y] = idx ++;
}
bool bfs()
{
queue<int> q;
memset(d, -1, sizeof d);
q.push(S), d[S] = 0, cur[S] = fist[S];
while(!q.empty())
{
int u = q.front(); q.pop();
for(int i = fist[u]; i != -1; i = line[i].nxt)
{
int v = line[i].to;
if(d[v] == -1 && line[i].flow)
{
d[v] = d[u] + 1;
cur[v] = fist[v];
if(v == T) return 1;
q.push(v);
}
}
}
return 0;
}
int find(int u, int limit)
{
if(u == T) return limit;
int flow = 0;
for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
{
cur[u] = i;
int v = line[i].to;
if(d[v] == d[u] + 1 && line[i].flow)
{
int t = find(v, min(line[i].flow, limit - flow));
if(!t) d[v] = -1;
line[i].flow -= t;
line[i ^ 1].flow += t;
flow += t;
}
}
return flow;
}
int dinic()
{
int res = 0, flow;
while(bfs()) while(flow = find(S, INF)) res += flow;
return res;
}
int main()
{
scanf("%d%d", &n, &m);
S = 0, T = n * m + 1;
memset(fist, -1, sizeof fist);
int tot = 0;
for(int i = 1; i <= n; ++ i)
for(int j = 1; j <= m; ++ j)
{
int w;
scanf("%d", &w);
if(i + j & 1)
{
add(S, get(i, j), w);
for(int k = 0; k < 4; ++ k)
{
int x = i + dx[k], y = j + dy[k];
if(x >= 1 && x <= n && y >= 1 && y <= m)
add(get(i, j), get(x, y), INF);
}
}
else add(get(i, j), T, w);
tot += w;
}
printf("%d
", tot - dinic());
return 0;
}
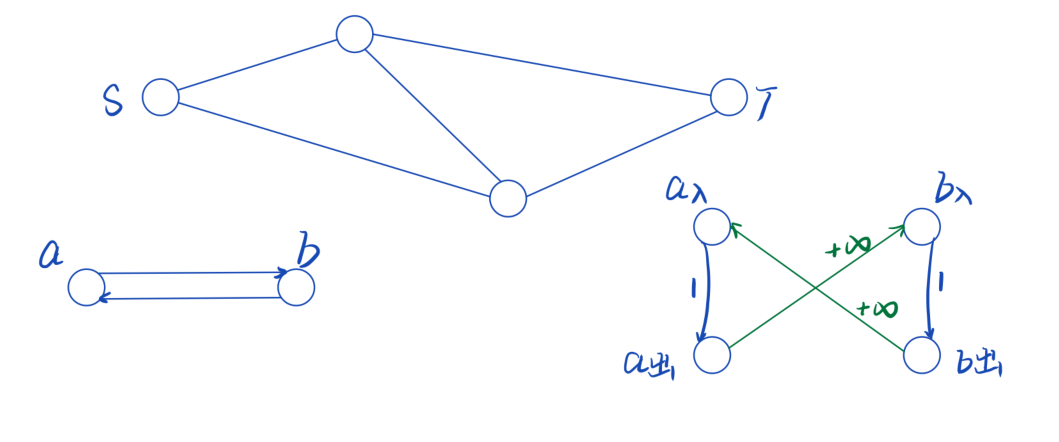
有线电视网络
使得两个点不连通, 枚举这两个点作为源点和汇点
要删去的是点,为了和割边产生联系,我们考虑拆点,删去某个点等价于把该点的入点到出点之间的边选为割边, 把不能被选为割边的边容量设为 (+infty)
- 每个点的入点到出点连一条容量为 (1) 的边
- 内部边不能被选为割边,它的容量设为 (+infty)
最小割即为使源点和汇点不连通时,需要删去的最少点数
#include <bits/stdc++.h>
using namespace std;
const int N = 50 * 2 + 10;
const int M = (50 * 50 + 50 + 10) * 2;
const int INF = 1e9;
int n, m, S, T;
struct Edge
{
int to, nxt, flow;
}line[M];
int fist[N], idx;
int cur[N], d[N];
void add(int x, int y, int z)
{
line[idx] = {y, fist[x], z};
fist[x] = idx ++;
line[idx] = {x, fist[y], 0};
fist[y] = idx ++;
}
bool bfs()
{
queue<int> q;
memset(d, -1, sizeof d);
q.push(S), d[S] = 0, cur[S] = fist[S];
while(!q.empty())
{
int u = q.front(); q.pop();
for(int i = fist[u]; i != -1; i = line[i].nxt)
{
int v = line[i].to;
if(d[v] == -1 && line[i].flow)
{
d[v] = d[u] + 1;
cur[v] = fist[v];
if(v == T) return 1;
q.push(v);
}
}
}
return 0;
}
int find(int u, int limit)
{
if(u == T) return limit;
int flow = 0;
for(int i = cur[u]; i != -1 && flow < limit; i = line[i].nxt)
{
cur[u] = i;
int v = line[i].to;
if(d[v] == d[u] + 1 && line[i].flow)
{
int t = find(v, min(line[i].flow, limit - flow));
if(!t) d[v] = -1;
line[i].flow -= t;
line[i ^ 1].flow += t;
flow += t;
}
}
return flow;
}
int dinic()
{
int res = 0, flow;
while(bfs()) while(flow = find(S, INF)) res += flow;
return res;
}
int main()
{
while(scanf("%d%d", &n, &m) == 2)
{
memset(fist, -1, sizeof fist);
idx = 0;
for(int i = 0; i < n; ++ i) add(i, n + i, 1);
for(int i = 1; i <= m; ++ i)
{
int a, b;
scanf(" (%d,%d)", &a, &b);
add(n + a, b, INF);
add(n + b, a, INF);
}
int res = n;
for(int i = 0; i < n; ++ i)
for(int j = 0; j < i; ++ j)
{
S = n + i, T = j;
for(int k = 0; k < idx; k += 2)
{
line[k].flow += line[k ^ 1].flow;
line[k ^ 1].flow = 0;
}
res = min(res, dinic());
}
printf("%d
", res);
}
return 0;
}