樽海鞘是一种透明的桶状生物,和水母比较相似。它通过吸水、喷水来移动的。由于它生活在寒带的深海里面,给我们的研究造成了一定的困扰。但是,这并不影响我们对它的研究。在深海里,樽海鞘是以樽海鞘链的形式存在,这就是我们感兴趣的群体行为之一。
首先,我们将樽海鞘链分为两组:1、领导者;2、追随者。
领导者就是樽海鞘链前端的部分;追随者就是樽海鞘链后端的部分。
首先,领导者的位置跟新公式:

最后,更新追随者位置
为了不误导大家,我给直接给出结果
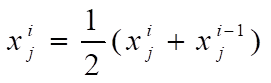
clc;
clear all;
close all;
%% 问题定义
CostFunction = @(x) sphere(x); % 目标函数
nVar = 5; % 变量的维数
VarSize = [1,nVar]; % 变量的矩阵大小
VarMin = -10; % 变量的下确界
VarMax = 10; % 变量的上确界
%% SSA参数
MaxIt = 1000; % 最大迭代次数
nPop = 50; % 种群大小
%% 初始化
% 樽海鞘模板
empty_slaps.Position = [];
empty_slaps.Cost = [];
empty_slaps.Best.Position = [];
empty_slaps.Best.Cost = [];
% 创建种群数组
slaps = repmat(empty_slaps,nPop,1);
% 初始化食物的适应度
Food.Cost = inf;
% 初始化种群
for i=1:nPop
% 生成随机解
slaps(i).Position = unifrnd(VarMin,VarMax,VarSize);
% 评价
slaps(i).Cost = CostFunction(slaps(i).Position);
% 更新最优个体
slaps(i).Best.Position = slaps(i).Position;
slaps(i).Best.Cost = slaps(i).Cost;
% 更新食物的位置
if slaps(i).Best.Cost < Food.Cost
Food = slaps(i).Best;
end
end
BestCosts = zeros(MaxIt,1);
%% SSA算法的主程序
it = 1;
while it < MaxIt+1
c1 = 2*exp(-(4*it/MaxIt)^2); % 设置参数
for i=1:nPop
if i <= nPop/2
c2=rand();
c3=rand();
%%%%%%%%%%%%% % Eq. (3.1) in the paper %%%%%%%%%%%%%%
if c3<0.5
slaps(i).Position =Food.Position + c1*((VarMax - VarMin)*c2 + VarMin);
else
slaps(i).Position =Food.Position - c1*((VarMax - VarMin)*c2 + VarMin);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
elseif i > nPop/2 && i < nPop+1
point1 = slaps(i-1).Position;
point2 = slaps(i).Position;
slaps(i).Position = (point2 + point1)/2;
end
end
for i=1:nPop
slaps(i).Position = max(slaps(i).Position,VarMin);
slaps(i).Position = min(slaps(i).Position,VarMax);
slaps(i).Cost = CostFunction(slaps(i).Position); % 计算每个体的适应度值
if slaps(i).Cost < slaps(i).Best.Cost
slaps(i).Best.Position = slaps(i).Position;
slaps(i).Best.Cost = slaps(i).Cost;
if slaps(i).Best.Cost < Food.Cost
Food = slaps(i).Best;
end
end
end
BestCosts(it) = Food.Cost;
disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCosts(it))]);
it = it + 1;
end
%% Results
figure;
% plot(BestCosts,'LineWidth',2);
semilogy(BestCosts,'LineWidth',2);
xlabel('Iterations');
ylabel('Best Cost');
grid on;
function z = sphere(x)
%% 目标函数
z = sum(x.^2);
end
