费用流练习

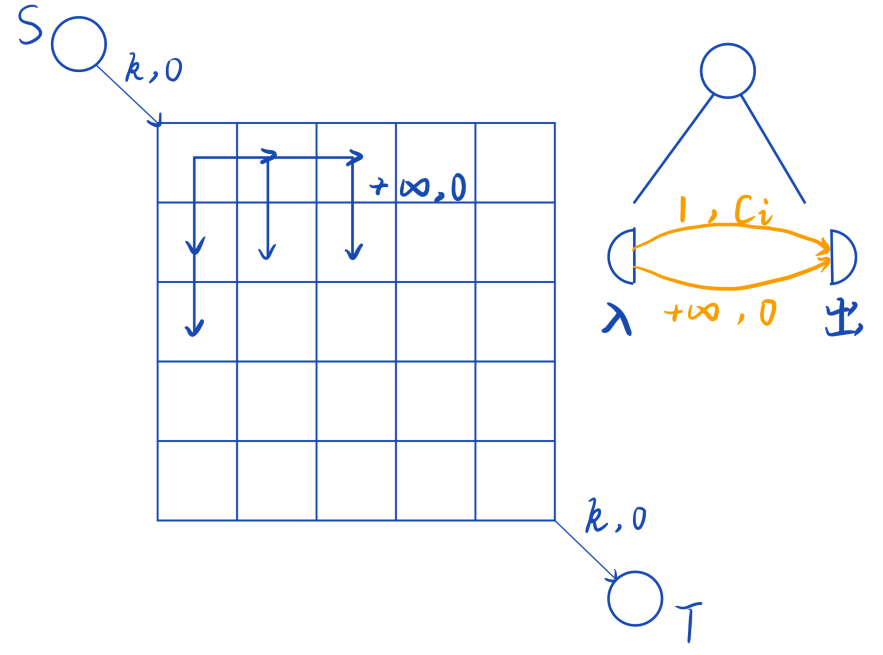
K取方格数

每个点可以走无限次，但只有一次有权值，考虑拆点，在入点和出点间建立两条边，只有一条有权值

• 从虚拟源点向左上角的点连一条容量为 (k) 费用为 (0) 的边
• 从右下角的点向虚拟汇点连一条容量为 (k) 费用为 (0) 的边
• 从当前点向下方和右方的点连一条容量为 (+infty) 费用为 (0) 的边
• 从每个点的入点到出点连一条容量为 (1) 费用为 (c_i) 的边
• 从每个点的入点到出点连一条容量为 (+infty) 费用为 (0) 的边
  

每个方案和最大可行流一一对应， 求最大费用最大流即可

#include <bits/stdc++.h>
using namespace std;

const int N = 50 * 50 * 2 + 10;
const int M = (50 * 50 * 4 + 10) * 2;
const int INF = 1e9;

int n, k, S, T;
struct Edge
{
	int to, nxt, flow, w;
}line[M];
int fist[N], idx;
int d[N], pre[N], incf[N];
bool st[N];

void add(int x, int y, int z, int w)
{
	line[idx] = {y, fist[x], z, w};
	fist[x] = idx ++;
	line[idx] = {x, fist[y], 0, -w};
	fist[y] = idx ++;
}

bool spfa()
{
	queue<int> q;
	memset(d, -0x3f, sizeof d);
	memset(incf, 0, sizeof incf);
	q.push(S), d[S] = 0, incf[S] = INF;
	while(!q.empty())
	{
		int u = q.front(); q.pop();
		st[u] = 0;
		for(int i = fist[u]; i != -1; i = line[i].nxt)
		{
			int v = line[i].to;
			if(line[i].flow && d[v] < d[u] + line[i].w)
			{
				d[v] = d[u] + line[i].w;
				pre[v] = i;
				incf[v] = min(line[i].flow, incf[u]);
				if(!st[v])
				{
					q.push(v);
					st[v] = 1;
				}
			}
		}
	}
	return incf[T] > 0;
}

int EK()
{
	int cost = 0;
	while(spfa())
	{
		int t = incf[T];
		cost += t * d[T];
		for(int i = T; i != S; i = line[pre[i] ^ 1].to)
		{
			line[pre[i]].flow -= t;
			line[pre[i] ^ 1].flow += t;
		}
	}
	return cost;
}

int get(int x, int y, int t)
{
	return (x * n + y) * 2 + t;
}

int main()
{
	scanf("%d%d", &n, &k);
	S = n * n * 2, T = n * n * 2 + 1;
	memset(fist, -1, sizeof fist);
	add(S, get(0, 0, 0), k, 0);
	add(get(n - 1, n - 1, 1), T, k, 0);
	for(int i = 0; i < n; ++ i)
		for(int j = 0; j < n; ++ j)
		{
			int c;
			scanf("%d", &c);
			add(get(i, j, 0), get(i, j, 1), 1, c);
			add(get(i, j, 0), get(i, j, 1), INF, 0);
			if(i + 1 < n) add(get(i, j, 1), get(i + 1, j, 0), INF, 0);
			if(j + 1 < n) add(get(i, j, 1), get(i, j + 1, 0), INF, 0);
		}
		
	printf("%d
", EK());
	return 0;
} 

志愿者招募

无源汇上下界最小费用可行流

#include <bits/stdc++.h>
using namespace std;

const int N = 1000 + 10;
const int M = (N * 2 + 10000 + 10) * 2;
const int INF = 1e9;

int n, m, S, T;
struct Edge
{
	int to, nxt, flow, w;
}line[M];
int fist[N], idx;
int d[N], pre[N], incf[N];
bool st[N];

void add(int x, int y, int z, int w)
{
	line[idx] = {y, fist[x], z, w};
	fist[x] = idx ++;
	line[idx] = {x, fist[y], 0, -w};
	fist[y] = idx ++; 
}

bool spfa()
{
	queue<int> q;
	memset(d, 0x3f, sizeof d);
	memset(incf, 0, sizeof incf);
	q.push(S), d[S] = 0, incf[S] = INF;
	while(!q.empty())
	{
		int u = q.front(); q.pop();
		st[u] = 0;
		for(int i = fist[u]; i != -1; i = line[i].nxt)
		{
			int v = line[i].to;
			if(line[i].flow && d[v] > d[u] + line[i].w)
			{
				d[v] = d[u] + line[i].w;
				pre[v] = i;
				incf[v] = min(line[i].flow, incf[u]);
				if(!st[v])
				{
					q.push(v);
					st[v] = 1;
				}
			}
		}
	}
	return incf[T] > 0; 
}

int EK()
{
	int cost = 0;
	while(spfa())
	{
		int t = incf[T];
		cost += t * d[T];
		for(int i = T; i != S; i = line[pre[i] ^ 1].to)
		{
			line[pre[i]].flow -= t;
			line[pre[i] ^ 1].flow += t;
		}
	}
	return cost;
}

int main()
{
	scanf("%d%d", &n, &m);
	S = 0, T = n + 2;
	memset(fist, -1, sizeof fist); 
	
	int last = 0;
	for(int i = 1; i <= n; ++ i)
	{
		int c;
		scanf("%d", &c);
		if(last > c) add(S, i, last - c, 0);
		else if(last < c) add(i, T, c - last, 0);
		add(i, i + 1, INF - c, 0);
		last = c;
	}
	add(S, n + 1, last, 0);
	
	for(int i = 1; i <= m; ++ i)
	{
		int a, b, c;
		scanf("%d%d%d", &a, &b, &c);
		add(b + 1, a, INF, c);
	}
	
	printf("%d
", EK());
	return 0;
}