中文分词系列（一） 双数组Tire树(DART)详解

1 双数组Tire树简介

---

 

双数组Tire树是Tire树的升级版，Tire取自英文Retrieval中的一部分，即检索树，又称作字典树或者键树。下面简单介绍一下Tire树。

1.1 Tire树

Trie是一种高效的索引方法，它实际上是一种确定有限自动机(DFA)，在树的结构中，每一个结点对应一个DFA状态，每一个从父结点指向子结点(有向)标记的边对应一个DFA转换。遍历从根结点开始，然后从head到tail，由关键词(本想译成键字符串，感太别扭)的每个字符来决定下一个状态，标记有相同字符的边被选中做移动。注意每次这种移动会从关键词中消耗一个字符并走向树的下一层，如果这个关键字符串空了，并且走到了叶子结点，那么我们达到了这个关键词的出口。如果我们被困在了一点结点，比如因为没有分枝被标记为当前我们有的字符，或是因为关键字符串在中间结点就空了，这表示关键字符串没有被trie认出来。图1.1.1即是一颗Tire树，其由字典{AC,ACE,ACFF,AD,CD,CF,ZQ}构成。

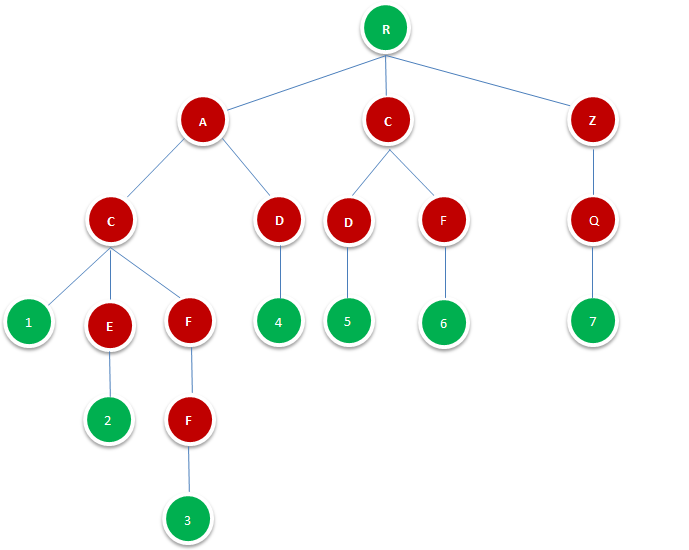
图1.1.1

图中R表示根节点，并不代表字符，除根节点外每一个节点都只包含一个字符。从根节点到图中绿色节点，路径上经过的字符连接起来，为该节点对应的字符串。绿色叶节点的数字代表其在字典中的位置

1.2 Tire树的用途

Tire树核心思想是空间换取时间，利用字符串的公共前缀来节省查询时间，常用于统计与排序大量字符串。其查询的时间复杂度是O（L），只与待查询串的长度相关。所以其有广泛的应用，下边简单介绍下Tire树的用途

 Tire用于统计：

 题目：给你100000个长度不超过10的单词。对于每一个单词，我们要判断他出没出现过，如果出现了，求第一次出现在第几个位置。

 解法 ：从第一个单词开始构造Tire树，Tire树包含两字段，字符与位置，对于非结尾字符，其位置标0，结尾字符，标注在100000个单词词表中的位置。对词表建造Tire树，对每个词检索到词尾，若词尾的数字字段>0,表示单词已经在之前出现过，否则建立结尾字符标志，下次出现即可得知其首次出现位置，便利词表即可依次计算出每个单词首次出现位置复杂度为O（N×L）L为最长单词长度，N为词表大小

 Tire用于排序

 题目：对10000个英文名按字典顺序排序

 解法：建造Tire树，先序便利即可得到结果。

1.3 针对Tire树的改进

Tire树虽然很完美，但缺点是空间的利用率很低，比如建立一颗ASCII的Tire树，每个节点的指针域为256，这样每个节点既有256个指针域，即使子节点置空，仍会有空间占用问题，解决办法是动态数组Tire树，即对子节点分配动态数组，生成子节点则动态扩大数组容量，这样便能有效的利用空间。

出于对Tire树占用空间的更有效利用，便引入了今天的主题：双数组Tire树，顾名思义，即把Tire树压缩到两个数组中。

双数组Tire树拥有Tire树的所有优点，而且刻服了Tire树浪费空间的不足，使其应用范围更加广泛，例如词法分析器，图书搜索，拼写检查，常用单词过滤器，自然语言处理 中的字典构建等等。在基于字典的分词方法中，许多开源

的实现都采用了双数组Tire树。

2 构造双数组Tire树

---

下面不如本文的主题双数组Tire树，其基本观念是压缩trie树，使用两个一维数组BASE和CHECK来表示整个树。双数组缺点在于：构造调整过程中，每个状态都依赖于其他状态，所以当在词典中插入或删除词语的时候，往往需要对双数组结构进行全局调整,灵活性能较差。 但对与，这个缺点是可以忽略的，因为核心词典已经预先建立好并且有序的，并且不会添加或删除新词，所以插入时不会产生冲突。所以常用双数组Tire树来载入整个核心分词词典。

　2.1 双数组的构造

Tire树终究是一颗树形结构，树形结构的两个重要要素便是前驱和后继，把Tire树压缩到双数组中，只需要保持能查询到每个节点的前驱和后继即可。Tire树中几个重要的概念

STATE：状态，实际为在数组中的下标 

CODE ： 状态转移值，实际为转移字符的 ASCII码

BASE  ：表示后继节点的基地址的数组，叶子节点没有后继，标识为字符序列的结尾标志

CHECK：标识前驱节点的地址

 

在DAT的构造过程当中，一般有两种构造方法：

1 动态输入词语，动态构造双数组。

定义2. 对于一个接收字符c从状态s移动到t的转移，在双数组中保存的条件是：

check[base[s] + c] = s

base[s] + c = t

以上为双数组中的核心转移公式，公式中s 和 t 均为状态state  

对于新插入字符串c₁c₂...c_n

树的构造过程如下，由根节点开始，加入到树中，加入方法即如上所述的状态转移方法。

base[root] + c₁ .code= t_{1 ，}check[t₁] = root 

base[t₁] + c₂.code = t₂ , check[t₂] = t₁

 ....

base[t_n-1] + c_n .code = t_n , check[t_n] = t_n-1

公式中的root t_i 即为 状态state，也就是在数组中的下标，如图2.1.2所示

 

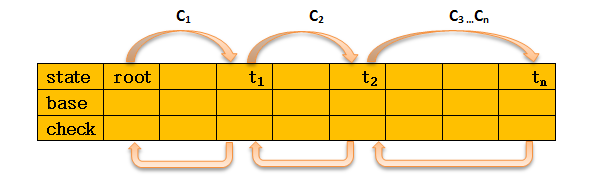
图2.1.1

root的base值一般是给定的，假定root在在位置0，base[root] = base[0] = 1

假设插入字符串AB， base[root]+ 'A'.code = 1+65 = 66,check[66] = 1,即 t₁ = 66，然后base[t₁] +'B'.code = t₂ ,因为t₂  可能被占用，所以要确保t₂ 的check值为空，即没有父节点，即插入 'B' 的就要在CHECK数组中找到一个空位置，即找到使check[base[t₁]+'B'.code] = 0的值begin，另base[t₁]=begin , base[t₁]+'B'.code即为状态t₂，另check[t₂] = t₁即可。

接下来依次插入其他字符序列，不同于静态构造，动态构造的插入过程中注意产生冲突的问题，比如现在Tire树由{AB，AC}构成，当插入AD时

首先要要找一个状态t为B C的基地址，若check[base[t]+'D'.code]  != 0,即base[t]可以作为BC基地址，而作为BCD的基地址却产生了冲突，因为base[t]+'D'.code已经被占用，解决办法是重新选择base[A]，重新寻找base[t],使得check[base[t]+'B'.code] = check[base[t]+'C'.code] = check[base[t]+'D'.code] = 0 即找到三个空位置重新放置三个子节点，可完成动态构造Tire树。 

2 已知所有词语，静态构造双数组；

_{这就是本文的重点了，静态构造Tire树，一般双数组的实现都会对算法做一个改进，下面的算法讲解主要参考开源实现dart-clone，dart-clone 也对双数组算法做了一个改进，即}

_{base[s] +c = t}

_{check[t] = base[s]}

不是原来的check[t] = s , 构造过程是 对于一组待插入的序列c_1...c_n,找到一个begin值，使得 begin+c₁.code...begin+c_n.code = t₁ ... t_n ,check[t₁] ... check[t_n] = base[s] = begin 即为c_1...c_n的基地址，而不是原来的 check[t =]s ，所以指向父节点的指针不是指向上一个状态，而是上一个状态s的base值  base[s],那么问题来了一个base[s]值只能作为一组children的基地址，若现在有第二组children也可以用base[s]作为基地址，如何防止这种冲突呢，解决方法就是做一个boolean数组 used[],一旦base[s]作为某组children的基地址，used[base[s]] = true，若产生冲突发现used[base[s]] = true，则说明已经作为父节点，则第二组children再重新寻找新的begin值。

_{dart-clone的另一个改进是另字符的code = ASCII+1，下面就是静态构造过程了，构造中首先要有一个字典，包含所有字符序列，并且一般情况下不会对构造完成的Tire树插入新字符序列}

对于由Dic = { AC,ACE,ACFF,AD,CD,CF,ZQ }构成的Tire树，其双数组如图2.1.1所示：由 dart-clone 生成的结果：

图2.1.1

其中i是下标，即为state，这里根据下标i可以看出BASE与CHECK数组的长度均达到了144，本图中只显示了BASE与CHECK中不为0的信息。

构造过程

1 建立根节点root,令base[root] =1

2 找出root的子节点 集{root.children_i }(i = 1...n) , 使得 check[root.children_i ] = base[root] = 1

3 对 each element in  root.children : 

　　1）找到{elemenet.children_i }(i = 1...n) ，注意若一个字符位于字符序列的结尾，则其孩子节点包括一个空节点，其code值设置为0找到一个值begin使得每一个check[ begin_i + element.children_i .code] = 0

　　2）设置base[element.children_i] = begin_i

　　3）对element.children_i 递归执行步骤3，若遍历到某个element，其没有children，即叶节点，则设置base[element]为负值（一般为在字典中的index取负）

下面举一个实例，对字典Dic = { AC,ACE,ACFF,AD,CD,CF,ZQ }建立Tire树，图1.1.1展示了其树形结构

1 遍历字典，找到root的所有children，在Dic中为{A C Z}，因为首次插入，直接设置其三个子节点的check值=1 root经过A  C  Z 的作用分别到达三个状态 t₁  t₂  t₃

状态t₁由条件 ‘A’ 触发，找到‘A’的子节点值{C D},找一个begin值，使得check[begin + 'C'.code] = check[begin +'D',code] = 0,这里 base[t₁] = begin = 2，状态t₁ =67,t₁下一状态为t₄ = base[t₁]+ 'C'.code ,t₅ = base[t₂] +'D'.code

继续向下便利，不断添加字符，状态转移，递归的对BASE与CHECK赋值，注意叶节点没有儿子，则设置其base值为-index , 最终便得到由两个数组表示的Tire树。

图2.1.2表示不同于图1.1.1，图2.12.使用DFA的形式来描绘，节点表示state，字符作为转移条件，不同字符触发不同的state，由图可见，一个转移状态对应一个state，在实现过程中，可以把2者结合起来，图2.1.2就会变成图1.1.1的形式了

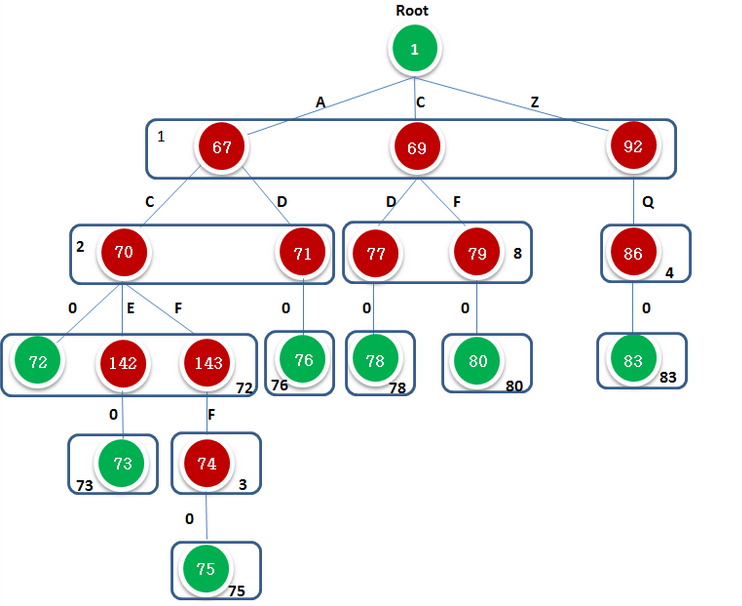
图2.1.2

注意：对于叶节点leaf.code = 0，标识为词尾

1 对于有相同父节点的children，其有相同的基地址值，如状态 67 69 92的check值= base[root] = 1

2 每个节点表示一个状态，子节点的check值即为父节点的base值

3 叶子节点的code值为0，叶子节点代表一个字符序列的结尾 且base[leaf] = -index

4 对于depth = 2 的节点 其基地址为1 ，1+'A'.code  1+'B'.code  1+'C'.code 为三个状态在数组中的位置 分别为 67 69 92

5 对叶节点t_leaf , check[t_leaf] = t_leaf， 因为到叶节点的转移字符leaf.code = 0,寻找begin值时，begin + leaf.code =t_leaf ,check[begin+ leaf.code] = begin ， 由于leaf.code = 0 , 则有begin = t_leaf，即check[t_leaf] = t_leaf

　2.2Tire树的查询

有了如上的构建过程，查询就会变的很easy

只需牢记：

base[s] + c = t

check[t] = base[s] 

当有 base[s] == t 时说明 c=0 ，即遇到了叶子节点，这时，记录下其位置index，然后输出Dic[index]即为匹配出来的dic中的词