csp-s模拟测试93T2口胡(蒟蒻的口胡大家显然就不用看了吧

我们先证正确性,再证复杂度

以下记$left langle i,j ight angle$为考虑$left [ i,j ight ]$的点时的最优决策

$left langle i,j ight angle$由$left langle i,j-1 ight angle$转移的

先放棵树

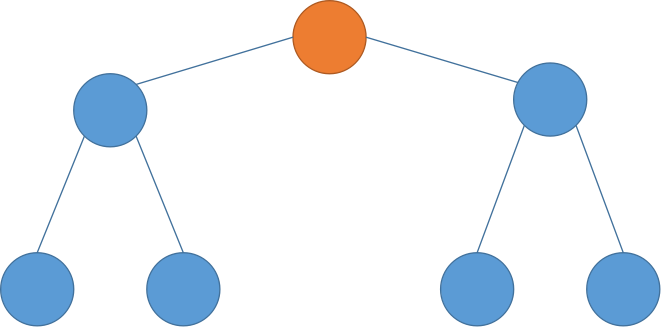
那个橙色的就是$left langle i,j-1 ight angle$

此时根是其他任意一个点都不会比现在更优

现在我们要在这颗树上插入点$j$,

显然$j$是这颗树中最大的点

那么这个点只会被插入到图示绿色区域内

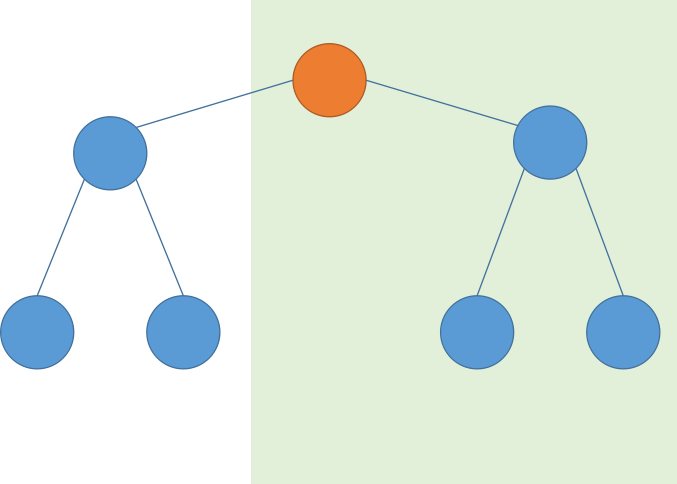
此时绿色区域中会有一个更深的点,

通过将绿色区域中某一点换为根可能会使答案变优,

但将白色区域的点换为根一定不优

所以$left [left langle i,j-1 ight angle,j  ight ]$为$left langle i,j ight angle$的可行区间

同理$left [i,left langle i+1,j ight angle  ight ]$为另一可行区间

有因为$left langle i,j-1 ight anglegeqslant i,left langle i+1,j ight angleleq j$

所以$left langle i,j ight angle$的可行区间为:$$left [ left langle i,j-1 ight angle,left langle i+1,j ight angle ight ]$$

然后是复杂度

考虑枚举每一个$len$

我们会更新$left langle i,j ight angle,left langle i+1,j+1 ight angle, cdots$

在更新$left langle i,j ight angle$时

我们会用到$left [left langle i,j-1 ight angle,left langle i+1,j ight angle  ight ]$

更新$left langle i+1,j+1 ight angle$时

我们会用到$left [left langle i+1,j ight angle,left langle i+2,j+1 ight angle  ight ]$

所以一个点最多被用两次

枚举$len$是$Theta (n)$的

所以总的来说是$Theta (n^{2})$的