这篇主要是讲对树的一些简单操作
1 练习:二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
这题主要是用递归并记录下返回值,如下:
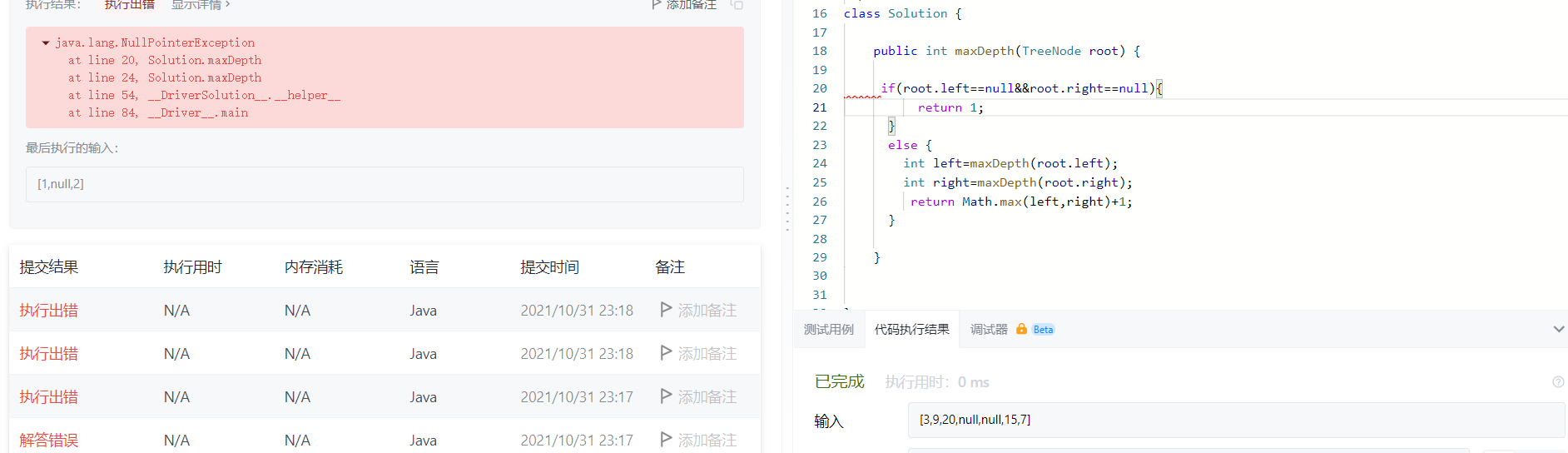
第一局,有点麻

原因,空指针异常,root成为叶子节点之后是没有左右子节点的,所以再深入递归一层,代码如下
class Solution {
public int maxDepth(TreeNode root) {
if(root==null){
return 0;
}
else {
int left=maxDepth(root.left);
int right=maxDepth(root.right);
return Math.max(left,right)+1;//本函数每一层都返回一个int相当于在每一个节点都判断左右子树的大小最大者留下,
}
}
2 练习:二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明:叶子节点是指没有子节点的节点。
这就同理可得了:

这玩意儿还有点小特殊,同理不行了,考虑考虑哪里不行
如果上述这么求的话,没有左孩子的分支会算为最短深度。
所以,如果左子树为空,右子树不为空,说明最小深度是 1 + 右子树的深度。
反之,右子树为空,左子树不为空,最小深度是 1 + 左子树的深度。 最后如果左右子树都不为空,返回左右子树深度最小值 + 1 。
加如果左右子树都为空的话,要返回到上一级
代码如下:
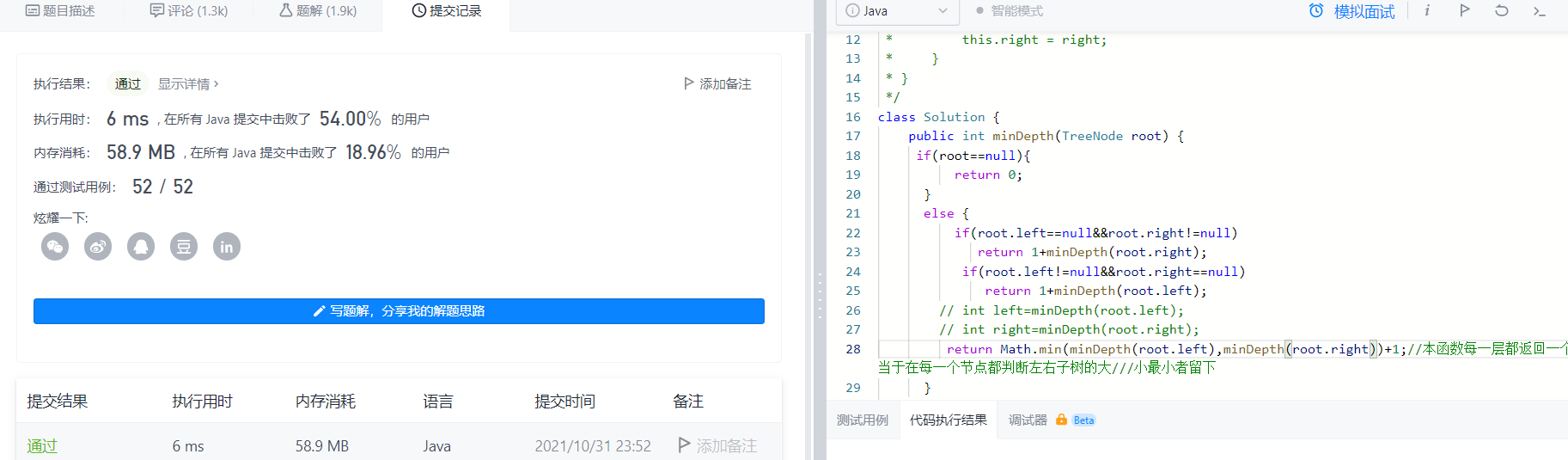
class Solution {
public int minDepth(TreeNode root) {
if(root==null){
return 0;
}
else {
if(root.left==null&&root.right!=null)
return 1+minDepth(root.right);
if(root.left!=null&&root.right==null)
return 1+minDepth(root.left);
// int left=minDepth(root.left);
// int right=minDepth(root.right);
return Math.min(minDepth(root.left),minDepth(root.right))+1;//本函数每一层都返回一个int相当于在每一个节点都判断左右子树的大///小最小者留下
}
}
}
没想到看似简单,还费了我一番功夫
未完,待更