树状数组是什么东东

          树状数组。求和，更新，求ith之前比a[i]小的元素个数！普通数组不行吗，行啊，关键树状数组快啊。贴个图：

                                                             

 

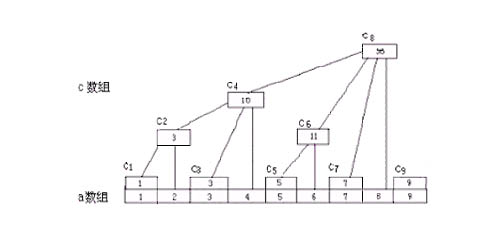
a数组为普通数组，c数组为属性数组，图要仔细研究研究，据说图明白了，离弄懂树状数组就不远了。

c1=a1;    (0001)

c2=a1+a2;(0010)

c3=a3（够shit的学校又要熄灯了，今天就到这里）(0011)

(继续：)
 c4=a1+a2+a3+a4    (0100)

c5=a5    (0101)

c6=a6+a5    (0110)

.....

.....

......上面每一个等式后面括号内的二进制码对应树状数组的下标 ，不知是否看出来等式左面的项数  等于   其下标二进制码  从右端开始出现的第一个1所代表的数值，再结合上面的图，是不是看的差不多了。树状数组的这种构造也正是其精华，上文讲到用其求和，或是求数组中（指的是普通数组a)第i个元素之前有多少个比他小的元素。当然要想做这些操作，首先要明白如何实现树状数组。下面有两个函数：

                           update（int i,int p)//i,p可以代表很多意义，还有看具体内容。这里可以认为是在初始化树状数组c  ，即在a[i]=p时

                           {

                                      for(;i<=n;i+=i&(-i))

                                            c[i]+=p;

                             }

                        循环语句中i+=i&(-1)   什么意思，i(&-i)   是求i对应的二进制码其最右面的一代表的数值（不懂得话自己可以求试试)

                        sum(int i)//求和函数

                       {

                              for(;i>0);i-=i(-i)

                                 S+=c[i];

                           return S;

                         }

其他的应用在此基础上发挥就行了