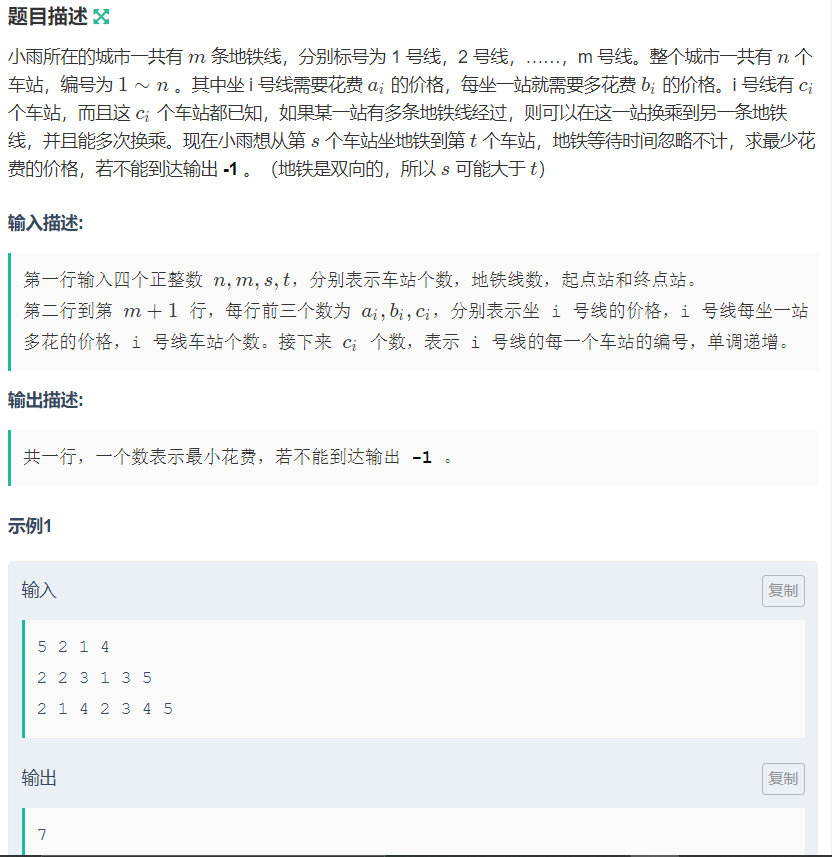
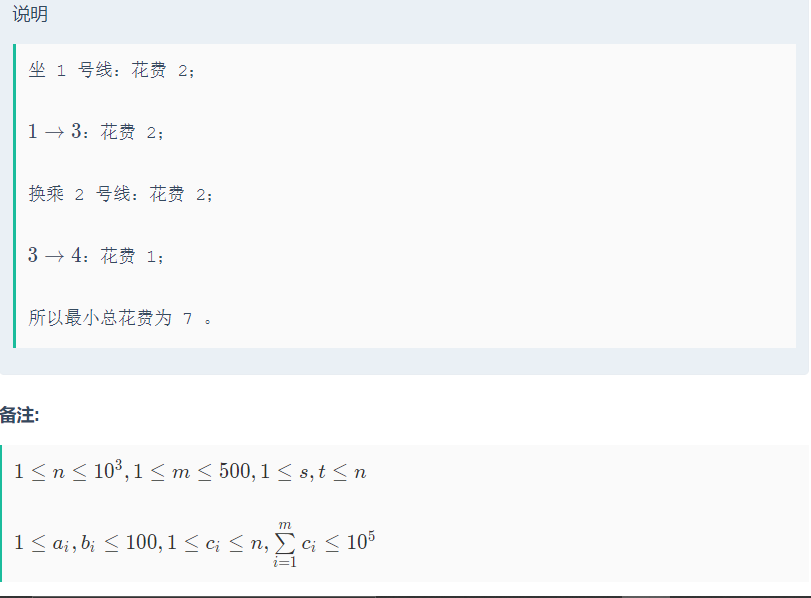
思路
如果考虑暴力建图的方法
对于每一条线路的每一个站点可到达的站点建边
在每条线路有1e5个站点的条件下显然是不现实的
如何解决建图的问题是此题的关键
因为有转车和车费逐步增加的情况存在
很容易想到分层图的概念
通过把路线看作不同的图层
就能把转车的概念转化为层与层之间的转化概念
令图层层数为 0 ~ m
其中第 m 层为中转线
所有的转车行为必须先转入中转层,再改换到其他的路线层
显然,去中转线的费用应为a[i],由中转层上其他车的费用为0
之后对于每一层的路线只要正常建图即可
CODE

1 #include <bits/stdc++.h> 2 #define dbg(x) cout << #x << "=" << x << endl 3 #define eps 1e-8 4 #define pi acos(-1.0) 5 6 using namespace std; 7 typedef long long LL; 8 9 template<class T>inline void read(T &res) 10 { 11 char c;T flag=1; 12 while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;res=c-'0'; 13 while((c=getchar())>='0'&&c<='9')res=res*10+c-'0';res*=flag; 14 } 15 16 namespace _buff { 17 const size_t BUFF = 1 << 19; 18 char ibuf[BUFF], *ib = ibuf, *ie = ibuf; 19 char getc() { 20 if (ib == ie) { 21 ib = ibuf; 22 ie = ibuf + fread(ibuf, 1, BUFF, stdin); 23 } 24 return ib == ie ? -1 : *ib++; 25 } 26 } 27 28 int qread() { 29 using namespace _buff; 30 int ret = 0; 31 bool pos = true; 32 char c = getc(); 33 for (; (c < '0' || c > '9') && c != '-'; c = getc()) { 34 assert(~c); 35 } 36 if (c == '-') { 37 pos = false; 38 c = getc(); 39 } 40 for (; c >= '0' && c <= '9'; c = getc()) { 41 ret = (ret << 3) + (ret << 1) + (c ^ 48); 42 } 43 return pos ? ret : -ret; 44 } 45 46 const int maxn = 2e6 + 7; 47 const int inf = 0x3f3f3f3f; 48 49 int head[maxn << 1], edge[maxn << 1], w[maxn << 1], nxt[maxn << 1]; 50 int cnt; 51 52 inline void BuildGraph (int u, int v, int c) { 53 cnt++; 54 edge[cnt] = v; 55 nxt[cnt] = head[u]; 56 w[cnt] = c; 57 head[u] = cnt; 58 } 59 60 struct node { 61 int u,v; 62 bool operator <(const node &t) const { 63 return u > t.u; 64 } 65 }; 66 67 int n,m,s,t,k; 68 int dis[maxn << 1]; 69 bool vis[maxn << 1]; 70 71 priority_queue<node> q; 72 73 void dijkstra(int s) { 74 memset(dis, 0x3f, sizeof(dis)); 75 dis[s] = 0; 76 node temp; 77 temp.u = 0; 78 temp.v = s; 79 q.push(temp); 80 while(!q.empty()) { 81 int u = q.top().v; 82 int d = q.top().u; 83 q.pop(); 84 if(vis[u]) continue; 85 vis[u] = true; 86 for (int i = head[u]; i; i = nxt[i]) { 87 int v = edge[i]; 88 int c = w[i]; 89 if(dis[v] > dis[u] + c && !vis[v]) { 90 dis[v] = dis[u] + c; 91 node p; 92 p.u = dis[v], p.v = v; 93 q.push(p); 94 } 95 } 96 } 97 } 98 99 int a[maxn << 1], b[maxn << 1], c[maxn << 1]; 100 101 int main() 102 { 103 read(n); read(m); read(s); read(t); 104 for ( int i = 1; i <= m; ++i ) { 105 read(a[i]); read(b[i]); read(c[i]); 106 int u = 0, v = -1; 107 for ( int j = 1; j <= c[i]; ++j ) { 108 read(u); 109 if(~v) { 110 BuildGraph((i - 1) * n + u, (i - 1) * n + v, b[i]); 111 BuildGraph((i - 1) * n + v, (i - 1) * n + u, b[i]); 112 } 113 v = u; 114 BuildGraph((i - 1) * n + u, n * m + u, 0); 115 BuildGraph((n * m) + u, (i - 1) * n + u, a[i]); 116 } 117 } 118 dijkstra(n * m + s); 119 int ans = INT_MAX; 120 for ( int i = 1; i <= m; ++i ) { 121 ans = min(ans, dis[n * i + t]); 122 } 123 if(ans == inf) { 124 puts("-1"); 125 return 0; 126 } 127 cout << ans << endl; 128 return 0; 129 }
