杨辉三角与二项式定理

首先杨辉三角是啥：

利益方面，把 （a + b）^n 展开，将会得到一个关于x的多项式：

　　（a + b）^0 = 1

　　（a + b）^1 = a + b

　　（a + b）^2 = a^2 + 2*a*b + b^2

　　（a + b）^3 = a^3 + 3*a^2*b + 3*a*b^2 + b^3

　　（a + b）^4 = a^4 + 4*a^3*b + 6*a^2*b^2 + 4*a*b^3 + b^4

系数正好跟杨辉三角一致。一般的，有二项式定理：

　　

所以，（a + b）^n 是n个括号连乘，每个括号里任选一项乘起来都会对最后的结果有一个影响。如果选择了 k 个 a，就一定会选择 n - k个 b,最后的项也就是 a^(n-k)*b^k 。然而从n个a里选择k个有多少种方法呢？

有 C（k ， n）种方法，这就是组合数的定义。

　　给定 n ,如何求出（a + b）^n 中所有项的系数呢？一个方法是用递归，根据杨辉三角中不难发现的规律，可以写出程序：

memset(c,0,sizeofcv));
for(int i = 0;i <= n;i++){
    c[i][0] = 1;
    for(int j = 1;j <= i;j++)
        c[i][j] = c[i-1][j-1] + c[i-1][j];
}

（以上的算法的时间复杂度是O（n^2） ）

另一个方法是利用等式C( k, n) = ( n - k + 1) / ( k ) * C( k-1, n)，从C( 0, n) = 1开始从左往右递推，如下：

c[0] = 1;
for(int i = 1;i <= n;i++)
    c[i] = c[i-1]*(n-i+1)/i;

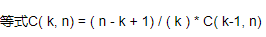可能不明显，却容易用组合数公式 C（k , n）= n! /( k! * (n - k)! )。