A-Uint47 calculator(快速乘)
题意:
定义一堆变量然后进行加减乘除运算
思路:
这题难的地方在乘法,会超出long long的范围,所以要用到快速乘(原理跟快速幂类似)

#include<iostream> #include<algorithm> #include<vector> #include<map> #include<string> #define Endl endl using namespace std; typedef long long ll; const ll mod=1ll<<47; map<string,ll> m; string s1,s2,s3; ll qm(ll a,ll b) { ll ans=0; while(b){ if(b%2) ans=(ans+a)%mod; a=(a+a)%mod; b/=2; } return ans; } int main() { ll num; while(cin>>s1>>s2){ if(s1=="def") cin>>num; else{ cin>>s3; if(s1=="add") num=(m[s2]+m[s3])%mod; if(s1=="sub") num=(m[s2]-m[s3]+mod)%mod; if(s1=="mul") num=qm(m[s2],m[s3]); if(s1=="div") num=m[s2]/m[s3]; if(s1=="mod") num=m[s2]%m[s3]; } if(num<0) num+=mod; m[s2]=num; cout<<s2<<" = "<<num<<endl; } return 0; }
D-Number theory(线段树)
题意:
初始化x=1,有两种操作:M yi: x = x * yi 与 N di: x = x / ydi ,输出每次操作之后的x的值
思路:
用线段树维护乘积和,线段树下标对应的值就为yi
每次进行M操作时将yi进行修改,N操作则将对应的ydi修改为1,每次修改输出Tree[1]即为乘积

#include<iostream> #include<algorithm> using namespace std; typedef long long ll; const int maxn=1e5+20; ll tree[maxn<<2],m; void push_up(int rt) { tree[rt]=(tree[rt<<1]*tree[rt<<1|1])%m; } void update(int pos,int l,int r,int val,int rt) { if(l==r){ tree[rt]=val; return; } int mid=(l+r)>>1; if(pos<=mid) update(pos,l,mid,val,rt<<1); else update(pos,mid+1,r,val,rt<<1|1); //push_up(rt); tree[rt]=(tree[rt<<1]*tree[rt<<1|1])%m; } int main() { int t,k,n; char s[9]; scanf("%d",&t); while(t--){ scanf("%d%lld",&n,&m); for(int i=1;i<=n<<2;i++) tree[i]=1; for(int i=1;i<=n;i++){ scanf("%s%d",&s,&k);; if(s[0]=='M') update(i,1,n,k,1); else update(k,1,n,1,1); cout<<tree[1]<<endl; } } }
E-Traffic jam(最短路)
题意:
给一张无向图带权图,每个点在每个特定时段才能通行,从点s到点t的最短时间
思路:
正常跑dij,在进行松弛操作时,要判断点能否通行,不能通行的话边权要加上等待的时间之后看看能否松弛

#include<iostream> #include<algorithm> #include<cstring> #define inf 0x3f3f3f3f using namespace std; const int maxn=1005; int dis[maxn],m[maxn][maxn],a[maxn],vis[maxn]; int t,n,k,u,v,val,x,y; void init() { memset(vis,0,sizeof(vis)); memset(dis,inf,sizeof(dis)); memset(m,inf,sizeof(m)); for(int i=1;i<=n;i++) m[i][i]=0; } int dij(int s,int t) { dis[s]=0; //vis[s]=1; for(int i=1;i<=n;i++){ int temp=-1,mx=inf; for(int j=1;j<=n;j++){ if(!vis[j]&&dis[j]<mx){ temp=j; mx=dis[j]; } } if(t==-1) break; vis[temp]=1; for(int j=1;j<=n;j++){ if(!vis[j]&&m[temp][j]!=inf){ int d=dis[temp]; if((d%(2*a[temp]))>=a[t]) d+=(a[temp]-d%a[temp]); d=d+m[temp][j]; if(dis[j]>d) dis[j]=d; } } } return dis[t]; } int main() { scanf("%d",&t); while(t--){ scanf("%d%d",&n,&k); init(); for(int i=1;i<=n;i++) scanf("%d",&a[i]); for(int i=1;i<=k;i++){ scanf("%d%d%d",&u,&v,&val); m[u][v]=m[v][u]=val; } scanf("%d%d",&x,&y); cout<<dij(x,y)<<endl; } return 0; }
G-IoU(思维)
题意:
给两个矩形,问他们重叠部分的面积占合并之后的图形的面积的比值
思路:
直接求出合并之后的面积再减去原来两矩形的面积就为重叠的面积,注意要判断两个矩形是否重合

#include<iostream> #include<algorithm> #include<vector> #include<map> #include<string> #define Endl endl using namespace std; typedef long long ll; int main() { ll Cas,x1,x2,y1,y2,w1,w2,h1,h2,x3,y3,x4,y4; ll s,s1,s2; double rate; scanf("%lld",&Cas); while(Cas--){ cin>>x1>>y1>>w1>>h1; cin>>x2>>y2>>w2>>h2; x3 = max(min(x1,x1+w1),min(x2,x2+w2)); y3 = max(min(y1+h1,y1),min(y2,y2+h2)); x4 = min(max(x1,x1+w1),max(x2,x2+w2)); y4 = min(max(y1+h1,y1),max(y2,y2+h2)); if(x4>x3&&y4>y3) s=(y4-y3)*(x4-x3); else s=0; s1=w1*h1,s2=w2*h2; rate=(s*1.0)/(1.0*(s2+s1-s)); printf("%.2lf ",rate); } return 0; }
H-Chosen by god(组合数学)
题意:
进行n次攻击,每次攻击随机并等可能对敌人或敌人的侍从造成1单位伤害,敌人的血量无限,侍从的血量为m,问杀死侍从的概率是多少
思路:
进攻n次总共会有2n种可能,要杀死侍从至少要对其进攻m次,所以如果n<m,则概率为0
能杀死侍从的概率就有C(n,m)+C(n,m+1)+.....+C(n,n)种
所以概率就为C(n,m)+C(n,m+1)+.....+C(n,n)/2n

#include<iostream> #include<algorithm> using namespace std; typedef long long ll; const int mod=1e9+7; const int maxn=1e3+10; ll C[maxn][maxn]; ll pm(ll a,ll b) { ll ans=1; while(b){ if(b&1) ans=(a*ans)%mod; a=(a*a)%mod; b>>=1; } return ans; } ll get_C() { C[0][0]=1; for(int i=0;i<maxn;i++){ C[i][0]=C[i][i]=1; for(int j=1;j<=i;j++) C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod; } } int main() { get_C(); int Cas,n,m; ll ans,x; scanf("%d",&Cas); while(Cas--){ ans=0; scanf("%d%d",&n,&m); for(int i=m;i<=n;i++){ ans+=C[n][i]; ans%=mod; } x=pm(2,n); x=pm(x,mod-2)%mod; ans=(ans*x+mod)%mod; cout<<ans<<endl; } return 0; }
J-Mind control(组合数化简)
题意:
如果给编号为x的人一个蛋糕,那么编号大于x的人都会崇拜你,现在分发m个蛋糕,求对你产生崇拜人数的期望
思路:
每次分发蛋糕,产生崇拜人数只会与x的最小值有关,剩下的m-1个蛋糕可以在编号为(x,n]的人中随意分发,那么就可以推出期望的表达式为
但是这个公式的计算复杂度为O(n),1e6组询问下必TLE,所以还需对公式进行代换。
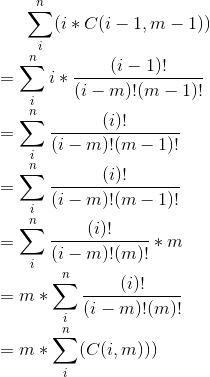
后面的和式为一个组合恒等式,根据C(m,m)=C(m+1,m+1)以及C(m+1,m)+C(m+1,m+1)=C(m+2,m+1)可得证明:
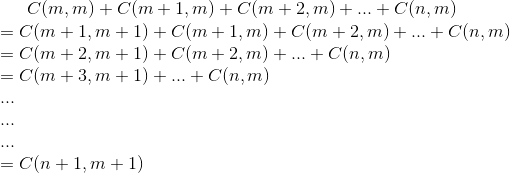
所以几个式子合并有:
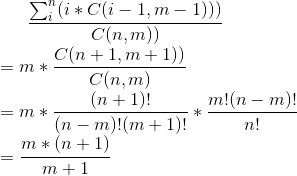

#include<iostream> #include<algorithm> using namespace std; typedef long long ll; const int mod=1e9+7; ll pow(ll a,ll b) { ll ans=1; while(b){ if(b&1) ans=(a*ans)%mod; a=(a*a)%mod; b>>=1; } return ans; } int main() { ll n,m,t,ans; scanf("%lld",&t); while(t--){ scanf("%lld%lld",&n,&m); if(m>n){ cout<<n<<endl; continue; } ans=(n+1)*m%mod; ll x=pow(m+1,mod-2)%mod; ans*=x; ans=(ans+mod)%mod; printf("%lld ",ans); } return 0; }
