给源图像增加边界
cv2.copyMakeBorder(src,top, bottom, left, right ,borderType,value)
src:源图像
top,bottem,left,right: 分别表示四个方向上边界的长度
borderType: 边界的类型
有以下几种:
BORDER_REFLICATE # 直接用边界的颜色填充, aaaaaa | abcdefg | gggg
BORDER_REFLECT # 倒映,abcdefg | gfedcbamn | nmabcd
BORDER_REFLECT_101 # 倒映,和上面类似,但在倒映时,会把边界空开,abcdefg | egfedcbamne | nmabcd
BORDER_WRAP # 额。类似于这种方式abcdf | mmabcdf | mmabcd
BORDER_CONSTANT # 常量,增加的变量通通为value色 [value][value] | abcdef | [value][value][value]
value: 仅仅是常量型边界才有意义
代码及结果如示:
import numpy as np import cv2 from matplotlib import pyplot as plt RED=[255,0,0] img = cv2.imread('/home/zh/pic/3.png') img1 = cv2.resize(img, (0,0), fx=0.5, fy=0.5) replicate = cv2.copyMakeBorder(img1, 10,100,100,100, cv2.BORDER_REPLICATE) reflect = cv2.copyMakeBorder(img1, 100,10,100,100, cv2.BORDER_REFLECT) reflect101 = cv2.copyMakeBorder(img1, 100,100,10,100, cv2.BORDER_REFLECT_101) wrap = cv2.copyMakeBorder(img1, 100,100,100,10, cv2.BORDER_WRAP) constant = cv2.copyMakeBorder(img1, 100,100,100,100, cv2.BORDER_CONSTANT, value=RED) plt.subplot(231),plt.imshow(img1),plt.title('ORIGINAL') plt.subplot(232),plt.imshow(replicate),plt.title('REFLECT') plt.subplot(233),plt.imshow(reflect),plt.title('REFLECT') plt.subplot(234),plt.imshow(reflect101),plt.title('REFLECT_101') plt.subplot(235),plt.imshow(wrap),plt.title('WRAP') plt.subplot(236),plt.imshow(constant),plt.title('CONSTANT') plt.show()
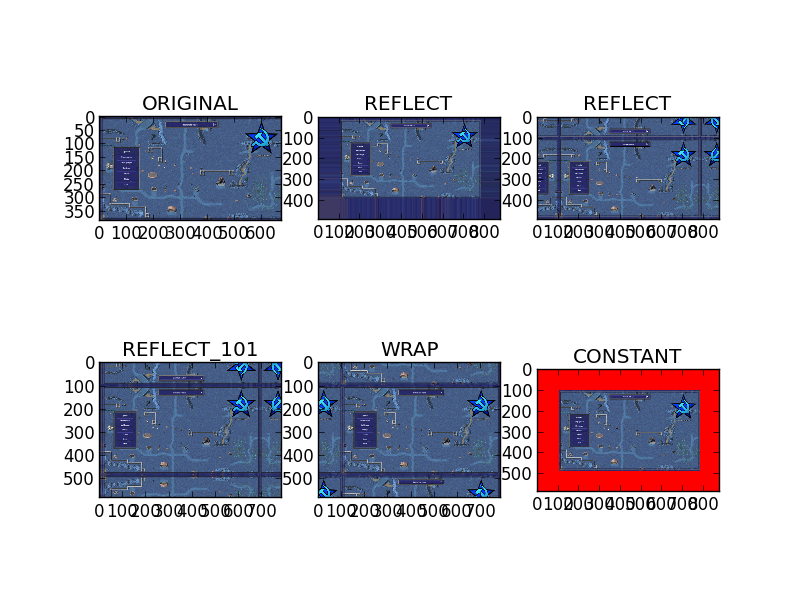
图像的几何变换:
常见的几何变换有缩放,仿射,透视变换,可以通过如下函数完成对图像的上述变换
dst = cv2.resize(src, dsize[, dst[, fx[, fy[, interpolation]]]]) dst = cv2.warpAffine(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]]) dst = cv2.warpPerspective(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]])
首先是缩放变换cv2.resize()
非关键字参数组有2个:src,dsize,分别是源图像与缩放后图像的尺寸
关键字参数为dst,fx,fy,interpolation
dst为缩放后的图像,fx,fy为图像x,y方向的缩放比例,
interplolation为缩放时的插值方式,有三种插值方式:
cv2.INTER_AREA # 使用象素关系重采样。当图像缩小时候,该方法可以避免波纹出现。当图像放大时,类似于 CV_INTER_NN 方法
cv2.INTER_CUBIC # 立方插值
cv2.INTER_LINEAR # 双线形插值
cv2.INTER_NN # 最近邻插值
仿射变换cv2.warpAffine()
非关键字参数有src, M, dsize,分别表示源图像,变换矩阵,变换后的图像的长宽
这里说一下放射变换的变换矩阵
位移变换矩阵为:
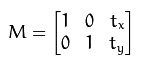
旋转变换矩阵:
标准旋转变换矩阵为
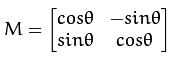 ,但该矩阵没有考虑旋转变换时进行位移以及缩放操作,OpenCV中的旋转变换如下:
,但该矩阵没有考虑旋转变换时进行位移以及缩放操作,OpenCV中的旋转变换如下:
![]() ,其中
,其中
OpenCV中提供了一个函数获得这样一个矩阵
M=cv2.getRotationMatrix2D(rotate_center, degree, scale)
rotate_center为一个2元的元组,表示旋转中心坐标,degree表示逆时针旋转的角度,scale表示缩放的比例
仿射变换矩阵:
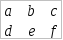
透视变换cv2.warpPerspective()
非关键字参数src, M, dsize分别表示源图像,变换矩阵,以及输出图像的大小
关键字参数为flags, borderMode, borderValue,这几个参数的意思理解的还不是很清楚,可以去
http://docs.opencv.org/modules/imgproc/doc/geometric_transformations.html 查找warpPerspective函数
透视变换矩阵一般不容易直接知道,能够直接知道的往往是变换前后的点的位置,因此,OpenCV中提供了getPersepectiveTransform()函数获得透视变换矩阵
M = cv2.getPerspectiveTransform(pts1, pts2)
pts1,pts2分别为变换前点的位置以及变换后点的位置
(其实所有的变换的变换矩阵都可以通过变换前后点的坐标得到,即通过上面这个函数,因为所有的变换都是透视变换中的特例而已)
最后用一个实例将上述变换函数作用呈现如下:
import numpy as np import cv2 from matplotlib import pyplot as plt #scaling: img = cv2.imread('/home/zh/pic/3.png') rows, cols, channels = img.shape res = cv2.resize(img, (cols/2, rows/2)) #Translation: # 1.shift M_shift = np.float32([[1,0,100],[0,1,50]]) img_shift = cv2.warpAffine(img, M_shift, (cols, rows)) # 2.rotate M_rotate = cv2.getRotationMatrix2D((cols/2, rows/2), 90, 1) img_rotate = cv2.warpAffine(img, M_rotate, (cols, rows)) # 3.affine pts1 = np.float32([[50,50],[200,50],[50,200]]) pts2 = np.float32([[10,100],[200,50],[100,250]]) M_affine = cv2.getAffineTransform(pts1,pts2) img_affine = cv2.warpAffine(img, M_affine, (cols, rows)) # 4.perspective pts3 = np.float32([[56,65],[368,52],[28,387],[389,390]]) pts4 = np.float32([[0,0],[300,0],[0,300],[300,300]]) M_perspective = cv2.getPerspectiveTransform(pts3,pts4) img_perspective = cv2.warpPerspective(img, M_perspective, (cols, rows)) print 'shift: ', M_shift print 'rotate: ', M_rotate print 'affine: ', M_affine print 'perspective: ', M_perspective plt.subplot(231),plt.imshow(img),plt.title('src') plt.subplot(232),plt.imshow(res),plt.title('scale') plt.subplot(233),plt.imshow(img_shift),plt.title('shift') plt.subplot(234),plt.imshow(img_rotate),plt.title('rotate') plt.subplot(235),plt.imshow(img_affine),plt.title('affine') plt.subplot(236),plt.imshow(img_perspective),plt.title('perspective') plt.show()
结果如下:
