第8章 参数化学习（parameterized learning）

第8章 参数化学习（parameterized learning）

前一章中，我们学习了KNN，虽然它简单但是不能从数据中学习，仅是利用了测试数据点和训练数据点之间的距离度量，这在数据量很大时，测试时间以及需要保存的数据量的缺陷将非常明显。因此，它既浪费了资源，又不能很好地构建机器学习模型。

相反，一个更理想的方法是定义一个机器学习模型，可以在训练期间从我们的输入数据中学习模式（要求我们在训练过程中花费更多的时间），但它的优点是可以用少量的参数来定义，这些参数可以很容易地用来表示模型，而不用考虑训练集的大小。这种学习类型称为参数化学习（parameterized learning），定义为：一个参数化模型是用一组固定大小的参数集合（独立于训练示例的大小）来总结数据的学习模型。无论你给参数化模型输入多少数据量，它都不会更改它所需要的参数数量。

本章中，我们回顾参数学学习的概念，并且怎样实现一个简单的线性分类器。就像在本书后面看到的，参数化学习是现代机器学习和深度学习算法的转折点。

1          线性分类介绍

本章的前半部分关注与线性分类的基本理论和数学教学，和更一般的参数化分类算法，这种算法从训练数据中学习模式。之后，提供一个用python实现的线性分类的例子来学习在代码中这些算法是如何工作的。

1.1    参数化学习的4个部件

从现在开始，参数化（parameterized）将分为几种情况，简单来说，参数化（parameterization）是定义一个给定模型必要参数的过程。在机器学习任务中，参数化涉及定义一个问题的4个关键部件：data、a score function、a loss function、weights and bias。

（1）    data：

这个部件就是我们要学习的输入数据，数据包括数据点和对应的类别标签，通常我们依据多维涉及矩阵来表示数据。

在多维设计矩阵中，每一行代表一个数据点，而每一列（通常是一个多维数组）对应一个不同的特征。例如考虑一个RGB颜色空间的100张图像的数据集，每个图像32*32像素。这个数据集设计的矩阵将是 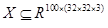 这里 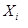 表示R中的第i个图像。依据这种表示，我们定义向量y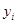， 表示数据集中第i个示例对应的标签。

（2）    a score function

评分函数（score function）接收数据作为输入，且将数据匹配到类别标签。例如在输入图像例子中，通过一个评分函数f，根据输入数据，得到一个预测的类别标签输出：

 

（3）a loss function

损失函数（loss function）量化我们预测的类别标签和真实的标签之间的一致程度。即这两类标签的一致成都越高，损失越低（或者至少在训练集上，精确度越高）。当训练一个机器学习模型时，我们的目标就是最小化损失函数，即增加分类精确度。

（3）    weights and biases

通常，用W表示的权重矩阵和用b表示的偏置向量，称为我们实际将要优化的分类器的权重或参数。基于评分函数和损失函数的输出，我们将调整和篡改权重和偏置的值来增加分类精确度。

基于你的模型类型，可能存在许多参数，但是在最基本的层面上，你通常面对的就是这4个参数化学习的构建模块。一旦我们定义了这4个关键部分，我们就可以应用优化方法（optimization methods），让我们找到一组参数W和b，使我们的损失函数相对于我们的评分函数最小化（同时提高我们数据的分类精度）。

接下来，我们看一下这些部件是如何工作在一起来构建一个线性分类器的，能够将输入数据转换为真正的预测。

1.2    线性分类：从图像到标签

这一节，我们将看一下参数化学习应用到机器学习的数学过程。首先，我们需要数据data，我们假定数据集由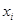 和每个图像对应的类别标签 表示。我们还将假定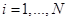 且 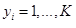，暗示在维度 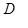上有 N个数据点，分属于K 个独立的类别中。

为了更精确，考虑第7章中的“Animals”数据集，在这个数据集中，总共有N=3000张图像，每张图像表示RGB空间的32*32像素，即D=32*32*3=3072个不同值，最后，有K=3个类别，分别为cats、dogs、pandas。

考虑到这些变量，我们必须定义一个评分函数f 将图像匹配到类别标签分数上。一种方法是通过简单的线性匹配来完成分数：

 

       我们考虑每一个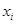表示大小为[D*1] 的单个的列向量（在这个例子中，将32*32*3转为3072的列表），我们的权重矩阵W将是大小为[K*D] （K为类别标签的数目）。最后偏置向量b大小为[K*1] ，偏置向量允许我们在不影响权重矩阵W的情况下，将我们的评分函数向一个方向或另一个方向上移动或调整。（意思是，在权重定了时，通过偏置b来调整到最佳位置？）

       在Animals例子中，图1表示线性分类函数f的例子。

 

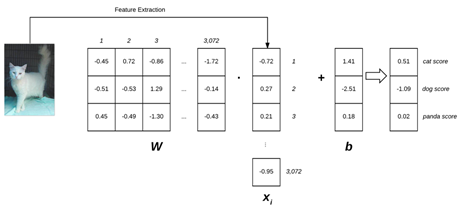
图1 线性分类的例子

       图1中左侧的输入图像为32*32*3大小，通过特征提取，将3D数组图像转变为1D列表，权重W包括三行（每行代表一类）和3072列（每一列表示图像的一个像素），加上偏置b后，就获得了最终的评分。

       实际上，依据参数化学习，我们仅需要控制的参数就是权重W和偏置b。因此，我们的目标就是同时利用评分函数和损失函数来优化权重W和偏置b提高分类精确度。

       优化权重矩阵精确的依赖于损失函数，但是通常涉及一些梯度下降（gradient descent）算法的形式。本章后面将回顾一下，但是梯度下降（和变种）的优化方法将在第9章讨论。但是，此时，我们知道只要给定了评分函数，我们也需要定义一个损失函数来告诉我们在输入数据上我们的预测有“多好”。

1.3    参数化学习和线性分类的优势

利用参数化学习有两个主要优势：

（1）              一旦我们训练好模型，就可以丢弃掉输入数据，仅需要保存权重矩阵W和偏置向量b，这将极大降低缓存大小。

（2）              对新的测试数据的分类是非常快的。为了执行预测，我们仅需要做的就是将权重矩阵W与输入 相乘，然后加上偏置b，获得结果。

1.4    用python实现的简单线性分类器

现在我们了解了参数化学习和线性分类的概念，下面使用python来应用一个简单的线性分类器。这个例子的目的不是从头来来从开始到结束训练模型，而是为了应用权重W和偏置b通过点乘对一个图像进行分类。代码见git仓库

https://github.com/shengqishi8787/Starter_Bundle.git下的chapter8

如果我们从头开始训练线性分类器，那么需要通过优化过程来学习权重W和偏置b的值。这里我们以Animals数据集的一张图片为例，那么图像转为向量为3072维，这里且以随机数来模拟权重W和偏置b。通过python linear_example.py将能够显示一张打了标签的图像。

实际上，我们从不需要自己初始化权重和偏置，而是，通过我们从头训练自己的机器学习模型，通过优化算法如梯度下降来优化和学习W和b。

2          损失函数的作用

为了通过我们的评分函数真正“学习”从输入数据到类标签的映射，我们需要讨论两个重要的概念：（1）损失函数；（2）优化方法。

本节接下来将讨论在神经网络和深度学习中常见的损失函数。在Starter Bundle的第9章将讨论基本的优化方法，在Practitioner Bundle的第7章将讨论更高级的优化方法。

本章只是损失函数的简要介绍，以及在参数化学习的作用。关于损失函数的更详尽的讨论以及数学化的严格推导见Andrew Ng’s Coursera course [76], Witten et al. [77], Harrington [78], and Marsland [79]。

2.1    什么是损失函数？

在最基本层面上，损失函数衡量一个给定分类器在分类数据集中输入数据点时有多好或多坏。如图2表示在CIFAR-10上两个分类器的模型的直观感受。

 

图2 两个模型的损失曲线示意图

损失越小，分类器在建模输入数据和输出类标签之间的关系方面做得越好（尽管我们可以在某种程度上过拟合（overfit）我们的模型——通过对训练数据进行过于紧密的建模，我们的模型失去了概括的能力，这种现象在第17章中讨论）。即损失越大，我们越需要做很多工作来增加分类精确度。

为了提高分类精确度，我们需要调整权重矩阵W和偏置b。如何更新这些参数是一个优化问题，这将在下一章中讨论。此时，只需知道损失函数可以用来度量我们的评价函数在分类数据点上有多好。

理想上，损失应当随着我们调整模型参数在时间上是降低的。从图2看出模型1开始稍微比模型2高，但之后快速下降且保持较低损失，我们说模型1可能是更期望的模型。“可能”是因为模型1还可能在输入数据集上过拟合，我们将在第17章讨论过拟合以及如何识别它。

2.2    多分类SVM损失

多分类SVMs损失（顾名思义）是由（线性）支持向量机（SVMs）启发而来，它使用一个评分函数f将我们的数据点映射到每个类标签的数字分数。函数f是一个简单的学习匹配：

 

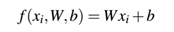
既然我们有了损失函数，我们需要确定这个函数（在给定W和b时）在做出预测时多好或多坏。为了更精确，我们需要损失函数。

当创建机器学习模型时，我们有设计矩阵X ，它的每一行表示要分类的数据点。在图像分类中，X 的每一行表示一个图像，我们说在 X中的第i个图像为 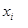。类似的， X对应的每一个类标签构成列向量y ，y 的值是标签的真实值，即是我们的评价函数希望正确预测的值。我们说对于一副图像 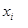，它对应的真实标签为 。

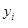不失一般性，我们用 简化评价函数：

 

这意味着我们可以通过第i个数据点获得第j个类别的预测分数：

 

使用这种语法，我们可以获得铰链损失函数（hinge loss function）:

 

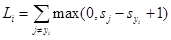
从本质上说，铰链损失函数是在所有不正确的类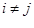（ ）上求和，并比较了我们的j类标签（不正确的类）和 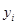类（正确的类）的评分函数s的输出。

当损失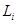 =0时， 分类正确。为了推导整个训练数据集上的损失，我们使用加权平均来计算：

 

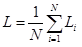
另一种相关的损失函数为平方铰链损失（squared hinge loss）:

 

平方项通过平方输出来惩罚。可看出，损失函数独立于数据集，更常见的是使用标准hinge loss，在一些数据集上使用squared hinge可能会获得较高准确率。但要知道，损失函数可被考虑为一个可以调整的超参数。

2.3    交叉熵损失和softmax分类器

虽然hinge loss是相当流行的，但在深度学习和卷积神经网络的背景下，你更有可能遇到交叉熵丢失（cross-entropy loss）和softmax分类器。

简单来说，softmax为每个类别标签给出概率，而hinge给出的是边界（margin）。对人类来说，概率要比边界评分更容易理解。

Softmax分类器是Logistic Regression二元形式的推广。

为了简洁性，评价函数中我们忽略偏置b：

 

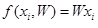
不像hinge loss，我们对每个类标签使用未归一化的log概率来解释得分，这里使用交叉熵损失来替换hinge loss function：

 

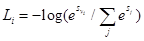
首先，我们的损失函数是将正确分类的负log概率最小：

 

这个概率可表示为：

 

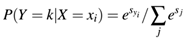
即我们可以获得单个数据点的评分函数：

 

通过指数求和的指数化和归一化是我们的softmax function。这里，忽略了归一化（regularization）项，这将在第9章讨论。

3          附录

[76] Andrew Ng. Machine Learning. https : / / www . coursera . org / learn / machine -learning (cited on pages 88, 132, 137, 141).
[77] Ian H. Witten, Eibe Frank, and Mark A. Hall. Data Mining: Practical Machine Learning Tools and Techniques. 3rd. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., 2011. ISBN: 0123748569, 9780123748560 (cited on page 88).
[78] Peter Harrington. Machine Learning in Action. Greenwich, CT, USA: Manning Publications Co., 2012. ISBN: 1617290181, 9781617290183 (cited on page 88).

[79] Stephen Marsland. Machine Learning: An Algorithmic Perspective. 1st. Chapman & Hall/CRC, 2009. ISBN: 1420067184, 9781420067187 (cited on page 88).