第11章 卷积神经网络（CNNs）

第11章 卷积神经网络（CNNs）

      我们回顾了整个机器学习和深度学习知识，现在我们学习CNNs（Convolutional Neural Networks）以及它在深度学习中的作用。在传统的前馈神经网络中，输入层的每一个神经元都与下一层的每一个输入神经元相连，我们称之为FC（fully-connected，全连接）层。但是，在CNNs中，我们直到网络中的最后一层才使用FC层。因此，我们可以将CNN定义为神经网络，该网络在专用的“卷积（convolutional）”层中交换，代替网络中至少一个层的“FC”层。

      一个激活函数例如ReLU将紧跟在卷积层后处理，且这种卷积==>激活的处理过程将持续（中间伴随着其它层类型的处理，这些层帮助减少输入值的长宽大小且帮助降低过拟合）直到到达网络的最后层次，然后我们实施一到两个FC层获得最终的输出分类。

      CNNs的每一层通常应用不同的过滤器集合，通常几百上千个，将这些结果组合起来，输入到下一层。在训练过程中，CNN自动的学习这些过滤器的值。

      在图像分类背景下，我们的CNN可以用来：在第一层中从原始像素数据检测边缘、在第二层中使用这些边缘检测形状、在网络的更高层中使用这些形状检测更高级的特征，如面部结构、汽车部件等。在CNN的最后一层，使用这些更高层的特征做出关于图像内容的预测。

实际上CNN给我们带来两个关键好处：局部不变性和组合性（local invariance and compositionality）。局部不变性的概念允许我们将分类一副图像看作是包含特定目标的过程，而不管图像中该目标出现在什么地方。我们通过“pooling layer”的使用来获得这种局部不变性，pooling层用对特定过滤器的高响应来标识输入卷（input volume）的区域。第二个优势是组合性，每个过滤器都将底层特征的部分组合到一起构成高层表示，这种组合允许我们的网络可以在网络的更深层次上学习到更富有的特征。例如，我们的网络可以从原始像素构建边缘、由边缘构建形状、由形状构建复杂物体，所有这些都在训练过程中自然地自动发生。这种从底层构建高层特征的概念正是CNN应用于计算机视觉的强大原因。

剩下内容，将讨论什么是卷积以及它在深度学习中的作用。之后将讨论CNN的构建块：层（layers）和你用于构建自己的CNN的层的类型。我们将通过查看常见的模式来总结本章，这些模式用于堆叠这些构建块以创建CNN架构，这些架构在一组不同的图像分类任务中表现良好。

在本章之后，我们可以（1）理解CNN、理解构建一个CNN的思考过程（2）使用一些CNN“配方”构建自己的网络架构。

1         理解卷积

本节中，我们提出了一些问题包括什么是图像卷积？它们能做什么？为什么我们要使用它？怎样将它们应用到图像上？卷积在深度学习上有什么作用？

对图像进行模糊/平滑、边缘检测、锐化…这些都是卷积，卷积是计算机视觉和图像处理中最重要、最基础的构建块之一。

在深度学习领域中，图像卷积就是两个矩阵对应元素相乘、然后求和。这就是卷积了：取两个矩阵（具有相同维度）、对应元素相乘、结果加到一起。在接下来我们将学到卷积、核（kernel）以及如何应用到CNN中。

1.1 卷积与互相关

具有计算机视觉和图像处理背景的读者可能将我描述的卷积作为互相关（cross-correlation）了，使用互相关代替卷积是在实际设计中使用的。一个二维的输入图像I和二维的核K的卷积为：

 

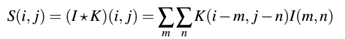
但是几乎所有的机器学习和深度学习库都使用简化的互相关函数：

 

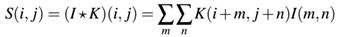
这两个的差异仅仅是在应用到图像上时，如何调整卷积核K，当互相关时，我们不需要翻转K，而卷积时需要翻转。

注意，在几乎所有深度学习库中都使用简化的互相关操作且称为卷积，这里我们也将使用这种术语约定。

1.2 大矩阵和小矩阵类比

一副图像是多维矩阵。我们的图像具有宽度width（列column）和高度height（行row）就像矩阵一样，但是图像还有深度deep即图像的通道channels。考虑到这些，我们称图像是大矩阵、称核kernel或卷积矩阵为小矩阵，小矩阵用于模糊、锐化、边缘检测和其它处理函数。特别的，小矩阵“坐”在大图像上部，并且从左往右、从上往下滑动，在原始图像的每一个(x, y)坐标上应用数学操作（如卷积）。

手动设计核来获得不同的图像处理函数是正常的。实际上，你可能熟悉模糊blurring (average smoothing, Gaussian smoothing, median smoothing, etc.), edge detection (Laplacian, Sobel, Scharr, Prewitt, etc.), and sharpening，所有这些都是用于手动设计的专门用于执行特定的功能。

那么，有自动学习这些类型过滤器的方式吗？甚至使用这些过滤器用于图像分类和目标检测吗？答案是肯定的，但在我们在那之前先更深入的学习核与卷积的知识。

1.3 Kernels核

 

图1 大矩阵与小矩阵示例

现在考虑如图1所示的图像大矩阵和核小矩阵的例子，核（红色区域）沿着原始图像从左往右、从上到下滑动。在原始图像的每一个(x,y)坐标处，我们停止并检查位于图像核中心的像素的邻域。之后取这个像素的邻域、将它们与核卷积、然后获得一个单个输出值。这个输出值位于输出图像的相同的(x,y)坐标处作为核的中心。

下面我们先看看核看起来是什么：

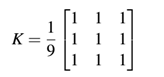
上面我们定义了一个3×3的核。核可以是任意的M×N大小，暗含了M和N都为奇整数。（应用于深度学习和CNNs的核大小一般都是N×N的核，这允许我们可以最有效的方式利用矩阵乘法。）

使用奇数核大小是确保在图像中心有一个有效的坐标(x,y)，如图2所示，在右侧核中，中心坐标0.5,0.5，这在图像中是不存在的。

 

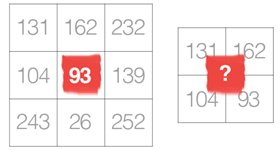
图2 奇数核和偶数核示例

1.4 卷积手动计算示例

在图像处理中，卷积需要三个参数：

（1）一个输入图像；

（2）将应用到图像上的核矩阵；

（3）存储卷积后的输出结果的输出图像。

卷积的计算很简单，即：

（1）从原始图像选择(x,y)坐标

（2）将核的中心放在该(x,y)坐标处

（3）将核与输入图像的对应坐标一一相乘，然后将这些乘积求和成为一个值。这些乘积求和的操作成为核输出（kernel output）。

（4）在输出图像上的与（1）中相同的(x,y)坐标处存储核输出。

例如，将上面定义的卷积核与图1中所在区域卷积：

 

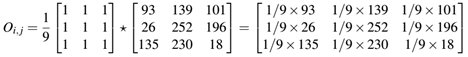
因此：

 

即在该卷积之后，我们设置输出图像O在(i,j)处的值Oi,j为132。这就是卷积计算了，卷就就是卷积核与卷积核在原始图像的覆盖区域的元素一一对应相乘求和的结果。

1.5 卷积python计算示例

为了更好地理解卷积，我们看实际代码如何处理。源代码不仅可以帮助来理解卷积计算是怎样的，还可以用于理解在训练CNN时卷积做了什么。现在可从git上下载chapter11/convolutions.py的文件，浏览代码。

通过执行python convolutions.py –image home.img即可。通过点击后可依次显示不同的模糊、锐化、边缘检测等手动卷积效果。

其中，除了手动设计的卷积计算，作者还给出了cv2.fiter2D(image, -1, K)的opencv调用结果用于对比查看卷积效果。

1.6 深度学习中卷积的作用

就像在上节中演示的，手动设计的卷积核都是很好地，但是有没有一种方式可以自动学习这些卷积核的参数呢？那么定义一种可以在输入图像上寻找并且可以最终学习到这些操作类型的机器学习算法是可能的吗？答案就是本书关注的算法：CNNs。

通过实施卷积过滤器、非线性激活函数、pooling和BP算法，CNNs可以在网络的较低级层上学习到可以检测边缘和类似块的结构的过滤器，之后使用这些边缘和结构作为“构建块”，最终在网络的较深层次上检测到高级对象（例如人脸、猫、狗等等）。

使用较低层学习到更高层特性的过程就是前面介绍的图像的组合性。但是CNN如何精确的做到的？答案是以有目的的方式堆叠一组特定的层。下一节，我们将讨论这些层的类型，并且看一些广泛用于许多图像分类任务中的层堆叠模式。

2         CNN构建块

就像在第10章介绍的，神经网络接收一个输入图像/特征向量（一个输入节点对应一个入口）且将它们通过一个通常是非线性激活函数的隐藏层传输。每个隐藏层也由多个神经元构成，且每一个神经元都全连接到前一层的神经元上。神经网络的最后一层也是全连接的且通常表示网络的最终分类输出。但是，这种传统神经网络通常工作在原始像素上，随着像素数目增加，输入节点数目急剧增加，且网络不能很好地分类性能。

相反， 我们可以使用利用输入图像结构的CNNs且定义一个更好的网络结构。不像标准的神经网络，CNNs的层组织成3D卷（volume）的三维形式：宽度、高度、深度（即图像的宽、高、通道，深度就是卷的第三个维度）。例如在CIFAR-10数据集中的图像：输入卷有32*32*3的维度。后续层中的神经元只会连接到其前面层的一个小部分区域（而不是标准神经网络的全连通结构）——我们称之为局部连通（local connectivity），它使我们能够在网络中保存大量的参数。最后输出层将是一个1×1×N的卷，表示图像分类成类别分数的单个向量。在CIFAR-10例子中，N=10，即最后一层是一个1×1×10的卷。

2.1 层类型

存在许多层类型用于CNNs，但是你最可能见到的是：

 

将这些层以特定的方式堆叠到一起就是CNN。我们常用一个文本图表描述一个CNN：INPUT => CONV => RELU => FC => SOFTMAX。这里描述了一个输入图像应用卷积层、之后激活层、全连接层，然后进入softmax分类器获得最终的分类概率。Softmax激活层常常在网络图表中忽略，因为假定是跟在最后的FC层之后的。

在这些层中，CONV和FC（以及较少使用的BN）是唯一包含在训练过程中学习的参数的层。RELU和DO层本身不考虑作为真正的“层”，包含在网络图表中只是为了使架构更清晰。Pool层与CON和FC层同等重要，因为它对一副图像的空间维度的改变具有重大影响。CONV、RELU、POOL和FC层在构建网络架构时是最重要的层。

2.2 Convolutional layer（卷积层）

CONV层是构建CNN的核心层。CONV层参数由K个可学习的过滤器（核）构成，每个核都有宽和高，通常相同。这些核很小，但是通常延伸到volume的整个深度上（即这些二维核计算时是在整个卷上计算？）。

对于CNN的输入，depth通常是图像的通道数。对于网络中更深层次的卷，其深度将是应用在上一层的过滤器的数量（我的理解是，后一层的输入深度为上一层卷积核的数量，当然这个卷积核的数量为多少根据具体CNN框架是具体问题具体分析的）。如图6所示，K个核的每一个核分别在输入图像上滑动计算卷积，和的输出值就是就是一个2D激活图（activation map）。

 

图6 激活图计算示意图

图6中左图表示要作用到输入图上的K个核，中图表示每个核都与输入图滑动计算卷积，右图表示每个核都输出一个激活图。在应用K个核作用到输入卷之后，我们计算得到了K个激活图，我们将这K个激活图沿着深度维度方向堆叠到一起构成了最终的输出卷，如图7所示，

 

图7 获得K个激活图，堆叠到一起构成网络下一层的输入卷

      输出卷的每一个输入都是神经元的输出，神经元只“看到”输入的一小块区域。通过这种方式，网络“学习”过滤器，当他们在输入卷中看到给定的空间位置上的特定类型的特征时，就会激活。在网络的较低层，当过滤器看到类似边或角的区域可能就会激活。那么，在网络的较高层，当存在高级特征如人脸的部分、狗的爪子、车的轮子时，过滤器就会激活。激活的概念就是当神经元在输入图像中看到特定模式时就“兴奋”且“激活”了。

      将小的过滤器与大的输入卷作卷积的概念在CNNs中有特殊的含义——具体的说，就是神经元的局部连接性（local connectivity）和感受野（receptive field）。在处理图像时，将当前卷中的神经元与上一个卷中的所有神经元连接起来往往是不现实的——有太多的连接、太多的权重，使得无法在空间尺寸较大的图像上训练深层网络。相反，在利用CNNs时，我们选择将每个神经元连接到输入卷的局部区域——我们称这个局部区域的大小为神经元的感受野（或简称为变量F）。

      例如，在CIFAR-10中输入卷是一个32×32×3的输入大小，即每个图像有32像素宽、32像素高和3深度（即RGB通道数目）。如果感受野是3×3大小，那么在CONV层中的每个神经元将连接到这个图像的一个3×3的局部区域，总共有3×3×3=27个权重值（记住，过滤器的深度延伸到输入图像的整个深度，这个例子为3个通道）。

      现在，让我们假设我们的输入卷的空间尺寸已经缩小到一个较小的尺寸，但是我们的深度现在更大了，因为在网络中使用了更多的过滤器，所以现在的卷尺寸是16×16×94。再次假定感受野的大小为3×3，那么在CONV层中的每个神经元对这个输入卷将总共有3×3×94=846个连接。简单的说，感受野F是过滤器的大小，即F×F的核与输入卷进行卷积。（注意注意注意！！！！这里说对于深度94，那么感受野3×3时，一个通道对应一个核，所以总共有3×3×94=846个参数，但是在现代CNN中，利用权值共享，即对于通道维度上的同一个感受野使用一个核代替所有通道上的核，即这94个核可由1个3×3的核代替，那么此时由于利用权值共享，我们的参数只有3×3=9个权值了。这应该在作者的后续书籍中会阐述，这里仅根据自己已知的理解，添加在这里。但是根据作者书籍中学到这里，我们默认还是以每个通道对应一个核的解释进行论述，慢慢深入理解。）

      此时，我们阐述了神经元的连接性，但是没有涉及输出卷的尺寸大小。有三个参数控制输出卷的大小：depth、stride和zero-padding尺寸。

（1）depth

      输出卷的深度控制在CONV层中连接到输入卷的局部区域的神经元（即过滤器）的数目。对于一个给定的CONV层，激活层的深度就是K，或者仅仅是当前层中我们要学习的过滤器的数目。“查看”输入的相同(x,y)位置的一组过滤器称为深度列（depth column）。

      （2）stride

      前面描述的小矩阵在大矩阵上滑动，这种描述类似于滑动窗口（sliding window）。在卷积描述中，我们通常每次滑动都只移动一步即一个像素，然后在感受野范围内使用K个卷积核计算深度卷，且产生一个3D卷。当创建CONV层时，通常使用一个stride步长（即滑动步长）称为S，大小一般S=1或S=2。较小的stride，将产生重叠的感受野、较大的输出卷；较大的stride，将产生不重叠的感受野、较小的输出卷。如表1与2所示的stride为1和2时的输出卷示例：

      

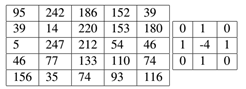
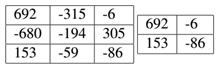
               表1 输入5×5，核3×3                        表2 左stride=1，右stride=2

我们可以看到，仅仅改变stride大小就可以改变输入卷的空间维度。根据后续内容，卷积层和pooling层是降低输入空间大小的主要方法。

（3）zero-padding

Pad即修补的意思，这里指的是在图像的四周“pad”上像素，可简化后续处理，zero-padding即在图像周围填上值为0的额外像素。使用zero-padding，通过这种技术可以使我们输出卷的大小与输入卷大小一致。Pad的大小通常用参数P表示。

当我们开始研究深度CNN体系结构时，这种技术尤其重要，这些体系结构在彼此之间应用了多个CONV过滤器。例如在表1中当S=1时，我们看到图中的左侧输出为3×3，要比输入卷5×5要小。如果我们在输入卷上使P=1，即在输入卷上下左右各补上1使之成为7×7的卷，则此时S=1时的输出卷为表3所示：

 

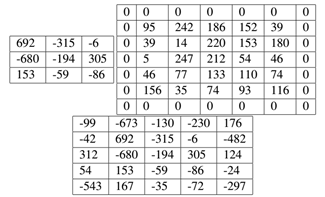
表3 3×3应用到pad=1的7×7卷积示例

没有zero padding，输入卷的空间维度将快速减少，即我们不能训练很深的网络（因为输入卷将太小而不能学习到有用的模式形式）。

将这些参数结合到一起，我们可以计算输出卷的大小作为数据卷大小（W，输入卷大小，通常为正方形）、感受野F、stride S、zero-pad大小P的函数。为了构建一个有效的CONC层，我们需要确保下述公式为整数，如果它不是一个整数，那么这些stride就被错误地设定了，神经元就不能被平铺成对称的大小：

((W – F + 2P) / S) + 1

举个例子，考虑AlexNet体系结构的第一层，它赢得了2012年ImageNet分类的挑战，对当前应用到图像分类的深度学习的热潮负有巨大的责任。论文[1]中，描述了如图8所示的CNN架构：

 

图8 文中描述的原始的AlexNet架构图

注意这里的第一层大小为224×224，由上述公式这是不可能的，因为(224 – 11 + 2*0) / 4 + 1 = 54.25不是一个整数，这很可能会对初学者造成困惑，作者最可能使用的输入大小为227×227，此时((227-11 +2(0))/4) + 1 = 55，正好是后一层的输入卷大小。这样的错误比你想象的更常见，所以在从出版物中实现CNNs时，一定要自己检查参数，而不是简单地假设列出的参数是正确的。

作为总结，CONV层和Karpathy[2]描述的一样优雅：

l  接受一个大小为W_input×H_input×D_input的输入卷（输入大小通常为正方形，即W_input = H_input）。

l  需要4个参数：

（1）过滤器K的大小（控制输出卷的深度）

（2）感受野大小F（用于卷积的K个核的大小，通常正方形，即为F×F大小）

（3）步幅stride：S

（4）zero-padding大小：P

l  之后为卷积层的输出即W_output×H_output×D_output这里：

——W_output = ((W_input - F +2P) / S) + 1
——H_output = ((H_input - F +2P) / S) + 1
——D_output = K

      我们将在3.1看到这些参数的设置。

2.3 Activation layer（激活层）

在CNN的每一个CONV层之后，我们将应用一个非线性激活层（activation layer），例如第10章中的ReLU、ELU或其它任何形式的Leaky ReLU变体。在网络图表中激活层通常用RELU表示，或仅仅ACT表示。激活层不是“层”技术（因为在激活层内没有需要学习的参数/权重）且有时候会在网络图表中省去，因为通常假定激活层紧跟在CONV层之后。作者倾向于在网络图表中明确的显示激活层，因为这样可以使网络中什么时候和怎么用激活函数很清晰，如下面的网络图表：INPUT => CONV => RELU => FC。

激活层接受大小为W_input×H_input×D_input的输入卷，然后应用到激活函数，如图9所示。由于激活层功能是像素一一对应处理的方式（in an element-wise manner），所以激活层的输出卷大小与输入卷大小相同：W_input = W_output，H_input = H_output，D_input = D_output。

 

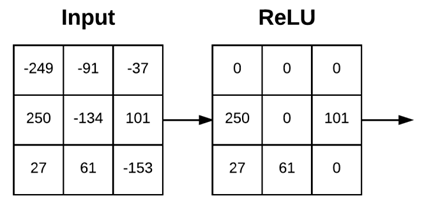
图9 应用ReLU函数为max(0, x)的示例

2.4 Pooling layer（池化层）

有两种方式可以降低输入卷的大小：stride>1的CONV层和POOL层。在CNN架构中通常在CONV层之间插入POOL层：

INPUT => CONV => RELU => POOL => CONV => RELU => POOL => FC

POOL层的主要功能是逐步缩小输入卷的空间尺寸大小（例如宽和高）。做这个可以降低网络中参数和计算的大小，即控制过拟合。

池化层使用最大（max）或平均（average）函数独立地操作输入的每个深度片（depth slice）。最大池化通常在CNN架构的中间使用来降低空间大小，而平均池化通常用于网络（例如GoogLeNet, SqueezeNet, ResNet）的最后层用来希望避免完全使用FC层。池化层最常见的类型是最大池化，尽管随着更奇异的微架构的引入，这种趋势正在改变。

通常使用的池化大小为2×2，尽管使用大的输入图像（像素大于200）的更深的CNN可能在网络早期使用3×3池化。我们通常设置的stride大小为S=1或S=2。图10是应用2×2大小最大池化和S=1的例子，注意这里对每个2×2的块我们取最大值，然后滑动一步，继续这种操作，即获得一个3×3的输出。

 

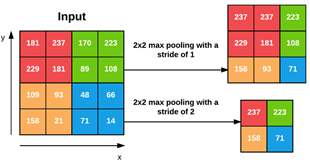
图10 max池化示例

我们可以通过增加stride大小进一步降低输入卷的大小，例如图10中stride=2时的例子中输出卷大小为2×2，通过每次滑动步幅为2。

作为总结，池化层接受大小为W_input×H_input×D_input的输入卷，该层通常需要两个参数：

l  感受野大小F（称为池化大小（pool size））

l  滑动步幅stride大小S

应用池化操作获得一个大小为W_output×H_output×D_output的输出卷：

l  W_output = ((W_input - F) / S) + 1

l  H_output = ((H_input - F) / S) + 1

l  D_output = D_input

现在的池化操作通常有：最大池化、平均池化和全局池化。实际中，常见到两种最大池化类型：

l  类型1：F=3, S=2称为重叠池化（overlap pooling）通常应用到具有大空间维度的输入图像上。

l  类型2：F=2, S=2称为非重叠池化（non-overlap pooling），这是最常见的池化类型且常应用到更小空间维度的图像上。

对于更小网络输入图像（例如32—64像素范围内）的网络架构中可能见到F=2, S=1的池化类型。

CONV还是POOL？

在2014年的文章[3]中，作者建议完全丢弃池化层并且仅仅应用具有大stride的CONV层对卷的空间维度进行下采样处理（downsampling，即降低维度？）。这个工作在不同数据集的演示中证明很好，包括CIFAR-10（小图像、少类别数目）和ImageNet（大输入图像、多类别数目）。这种趋势在ResNet也可得到验证。

如果可以避免FC层，在网络架构的中间不使用池化层并且仅在网络的末端使用平均池化正变得越来越常见。可能在将来的CNNs将不会有池化层，但是在此时，我们学习它、学些它的作用、应用到我们的网络架构中是很重要的。

2.5  Full-connected layers（全连接层）

FC层中的神经元与前一层的激活全部相连，因为它是第10章讨论的标准的前馈神经网络。FC层常常在网络层次的最后。在应用softmax分类器之前通常使用一到两个FC层，例如：

INPUT => CONV => RELU => POOL => CONV => RELU => POOL => FC => FC

这里我们在应用softmax分类器之前使用了2个FC层，softmax分类器将计算每个类别的最终输出概率。

2.6  Bach Normalization（批归一化）

第一次在文献[4]中介绍，批归一化层（简称为BN层），用于在传递到网络的下一层之前归一化给定输入卷的激活（activation）。

如果我们考虑x是我们激活的mini-batch，那么我们可以通过下式计算归一化的值：

 

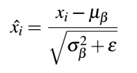
在训练过程中，我们可以在每一个mini-batch β中计算：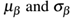

 

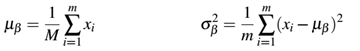
我们这里设置ε为一个小的正数例如1e-7来避免平方根为0。应用这个等式表明离开BN层的激活将具有近似零均值、单位方差。

在测试过程中，我们以在训练过程中计算的运行平均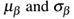代替mini-batch 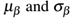。这确保了我们传递图片通过网络仍能获得精确的预测，而不会被来自在训练时间贯穿网络的最终mini-batch的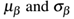偏离（biased）。

实践证明，BN对于减少训练神经网络的epoch数目是非常有效的。BN还有一个帮助稳定（stabilize）训练的额外好处，允许学习率和正则化强度的大的变化。当然，使用BN并不能减轻调整这些参数的需要，但是，这将通过使学习率和正则化程度降低、更易调整，从而使你的生活变得更加轻松。当在网络中使用BN时，你还会发现最终损失更低、损失曲线更稳定。BN的最大缺点是它增加了训练网络的时间（尽管它降低了epoch次数）。

我建议在几乎所有情况下使用BN，因为它确实有很大的不同。就像本书后面所说，与相同的不使用BN的网络架构相比，在网络架构中使用BN能帮助我们防止过拟合并且能够以更少的epoch次数获得极大的更高的分类精确度。

那么，BN层将用到哪个地方呢？在最早的文章[4]中他们将BN层放在激活层之前，基于这种机制，利用BN的网络架构像这样：

INPUT => CONV => BN => RELU ...

但是从统计学的角度看，这种BN层机制是没有意义的。这种BN层对CONV层之后的输出特征进行归一化，这个特征有可能是负的，也就是它可能被之后的ReLU层截断为0。那么我们将BN处理后的具有负值的零中心特性的BN结果输入到POOL层，则POOL层将会破坏我们应用BN层的零均值、单位方差的初衷。

因此，我们将BN层放在ReLU层之后，文献[5]确认将BN层放在激活层之后在几乎所有场景下将获得更高的精确度和更低的损失。那么这种结构类似于：INPUT => CONV => RELU => BN ...。

在作者的CNN实验中，这种放置确实能够稍微能够获得更高的精确度和更低的损失。在后面的实验中将对此说明。

2.7  Dropout（丢弃）

我们讨论的最后的层类型是Dropout。Dropout实际上是正则化的一种形式，目的是通过增加测试精确度可能降低训练精确度来防止过拟合。在我们训练集的每一次mini-batch中，我们以dropout层以概率p随机地将网络架构中从前一层到后一层的连接断开。图11为在给定的mini-batch中在两个FC层之间以概率p=0.5随机断开的示例：

图11 随机dropout与没有dropout的示例

在这次mini-batch的前向和后向计算完毕后，我们重新连接被dropout断开的连接，然后同样的另一个连接将开始dropout。

我们应用dropout降低过拟合的原因是明确的在训练时间内改变了网络架构。随机丢弃连接确保了当呈现一个给定模式时网络中没有单个节点负责“激活”。相反，dropout确保了当呈现一个类似输入时有多个、冗余节点将激活，这反过来使我们的模型更具泛化能力。

最常见的是将p=0.5的dropout层放在网络架构的FC层之间，这里最后的FC层假定是我们的softmax分类器：

但是就像在3.2中讨论的，我们也可能以更小的概率（例如p=0.10-0.25）将dropout放在网络的早期（通常跟随下采样，或者通过max pool或者CONV）。

3         常见的架构和训练模式

就像本章说的，CNN通常由4种主要层构成：CONV、ReLU、POOL、FC。取这些层且将它们按照特定模式堆叠在一起就形成了一个特定CNN架构。

CONV层和FC层（和BN）是唯一的实际可以学习参数的网络的层，其它层仅仅执行给定的功能。激活层和dropout层技术上不是层，但是常常包含在CNN架构图表中，是为了使操作更清晰明确，在这里我们也将使用这种描述。

3.1  层模式

到目前为止，最常见的CNN架构是堆叠一些CONV层和ReLU层，后面跟着POOL操作。我们重复这种次序直到卷的宽度和高度足够小，在这个点上我们应用一到两个FC层，那么我们可以获得最常见的CNN架构：

 

这里的*表示一个或多个，？表示可选的操作。通常的选择为：

l  0 <= N <= 3

l  M >= 0

l  0 <= K <= 2

下面是我们见到的一些CNN架构的模式例子：

 

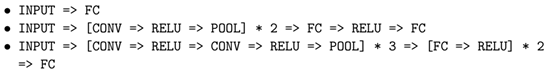
在第12章我们回顾一个只包含一个卷积层的非常浅的CNN：

 

下面是一个类似AlexNet的CNN架构：

 

对于更深的网络架构如VGGNet，我们可能在POOL之前堆叠多个CONV层，如：

 

一般来说，我们应用很深的网络架构时当我们（1）有大量标记的训练数据（2）分类问题具有足够的挑战。在应用一个POOL层之前堆叠多个CONV层，是在执行破坏性的池化操作之前，允许CONV层发展出（develop）更复杂的特性。

就像在ImageNet Bundle中讨论的，有很多从这些模式中推导出的奇异的网络架构，并且反过来创建了它们自己的模式。一些架构完全移除了POOL层操作，依赖CONV层对卷进行下采样，之后在网络的最后应用平均池化而不是FC层来获得到softmax分类器的输入。

如GoogLeNet、ResNet和SqueezeNet的网络架构时这种模式的强大的示例并且示例说明了如何移除FC层导致较少的参数和更快的训练时间。

这些类型的网络架构也在通道维度上堆叠和连接过滤器：GoogLeNet应用1×1、3×3和5×5的过滤器并且将它们在通道维度上堆叠在一起来学习多层特征。（这里，我认为是过滤器在每个通道上是不同的。）即这些架构更奇异也更高级。

如果你对这些更高级的CNN架构感兴趣，去看Practitioner Bundle；否则，你希望坚持这种基本的层堆叠模式直到你学习到了深度学习的基础。

3.2  经验法则

本节中我将回顾在构建自己的CNNs时的常见的经验法则。首先，输入层的的图像应当是正方形。使用正方形输入可以利用线性代数优化库。常见的输入层大小包括32 × 32、64 × 64、 96 × 96、 224 × 224、227 × 227和229 × 229（这里为了说明方便省略了通道数量）。

第二，输入层在应用第一次CONV操作之后还应该被2整除。你可以通过调整过滤器大小和步幅stride大小完成。“被2整除法则”使我们网络中的空间输入以一种有效的方式通过POOL操作可被方便的下采样。

一般来说，你的CONV层应该使用较小的过滤器尺寸如3×3和5×5。微小的1×1过滤器用于学习局部特征，但是仅用在更高级的网络架构中。较大的过滤器尺寸如7×7和11×11可用于网络的第一个CONV层（为了降低空间输入尺寸，假定你的图像大于200×200像素）；但是在这个初始化CONV层之后，过滤器尺寸应该急剧降低，否则你降低你的卷的空间尺寸将太快。

对于CONV层，你常使用步幅S=1，至少对于较小的空间输入卷来说（接收大的输入卷的网络可以在第一层CONV层使用S>=2）。使用S=1使我们的CONV层学习过滤器而POOL层负责下采样。但是注意，并不是所有网络都是这种模式，一些网络架构跳过了max pooling操作而且利用CONV层stride来降低卷尺寸。

作者个人的建议是倾向于将zero-padding应用到CONV层来确保输出维度尺寸匹配输入维度尺寸，这条规则唯一的例外是如果我们想通过卷积有目的降低空间尺寸。在堆叠多个CONV层时在每个输入都应用zero-padding，这在实际中被证明可以提高分类精确度。就像本书后面介绍的，keras库可以自动计算zero-padding，使得构建CNN架构更简单。

作者的第二个建议是使用POOL层（而不是CONV层）来降低输入的空间尺寸，至少直到你能在构建自己的CNN架构中更有经验。一旦你到达这一步，你就可以开始实施CONV层来降低空间输入尺寸并且尝试从你的架构中移除max pooling。最常见的，你将看到用2×2感受野尺寸和步幅S=2的max pooling，你也可能见到3×3的感受野尺寸。但是对于尺寸大于3的感受野大小是极其不常见的因为它会极大的破坏输入。

BN层在训练你的CNN时会多花费2~3倍的时间，但是作者建议在几乎所有场景下都使用BN层。尽管BN确实增加了训练时间，但是它倾向于“稳定”训练，能够更简单的调整其它超参数（当然，会有一些例外，作者将在ImageNet Bundle中详细描述这种例外架构）。作者将BN放在激活层之后，将BN插入到上面描述的常见的层模式：

 

你不需要在softmax分类器之前应用BN，因为在此时我们假定我们的网络已经在网络的早期学习到了有差别的特征。

DO层通常以50%的丢弃概率应用在FC层之间，你应该在你创建的几乎每一个架构中应用dropout。作者也喜欢在POOL层和CONV层之间包含dropout层（以非常小的概率，10%~25%），尽管这种方式不常见。由于CONV层的局部连接性，丢弃在这里不是很有效，但是作者发现它对克服过拟合很有帮助。

在充分熟悉这些传统的构建CNNs的方法之后，我们将在ImageNet Bundle中探索更高级的架构技术。

4         CNNs对转换、旋转、缩放具有不变性吗？

通常的问题是，CNNs对转换（translation）、旋转（rotation）、缩放（scale）的变化具有不变性吗？为什么CNNs具有如此强大的图像分类能力？为了回答这个问题，我们首先需要区分网络中的单个过滤器和最终经过训练的网络。CNN中的单个滤波器对图像旋转方式的变化并非不变的，我们将在ImageNet Bundle中的第12章进行论证。

但是一个CNN作为一个整体可以学习到当一个模式呈现在一个特定的方向时可以激活的过滤器。如图12所示：

 

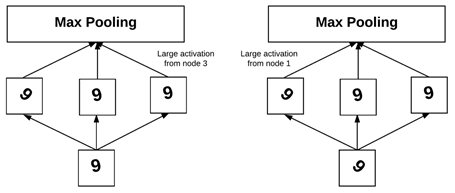
图12 CNN可学习到旋转变化时的过滤器

      我们看到存在于CNN中底部的数字9和CNN学到的一些中部的过滤器。图12左边的旋转10°左右的输入数字9被网络中的的一个过滤器学习到，该过滤器将被“点燃”且产生一个强的激活。这个大的激活值将在POOL层捕获并最终反映到最终分类上。类似的过程反映到图12右侧，有个近似旋转45°的数字9将被另一个过滤器捕获且进行同样的类似操作反映到最终分类器上。

      除非你的训练数据包含所有360°方向上的数字，否则你的CNN就不是真正的旋转不变性。类似的也是在缩放上，过滤器本身不是缩放不变性的，最可能的是你的CNN已经学会了一套过滤器，当模式以不同的规模存在时，它就会“点燃”。

但是，CNN对转换不变性是很擅长的。记住，过滤器会在输入时从左到右和从上到下滑动，当它碰到一个特定的边缘区域、角落或颜色斑点时会激活。在池化操作过程中，发现了这种大的响应，从而通过一个更大的激活来“击败”它的所有邻居。因此，可以把CNNs看作是“不在乎”一个激活fire的地方，简单是它fire了——以这种方式，我们在CNN内部自然地进行处理转换。Therefore, CNNs can be seen as “not caring” exactly where an activation fires, simply that it does fire – and, in this way, we naturally handle translation inside a CNN.

5         下一步

在下一章，我们将基于上面提到的层模式使用keras实现第一个CNN：ShallowNet。在将来的章节里还将讨论更深的网络架构，如LeNet架构以及VGGNet的变体。

6         文献参考

[1] Alex Krizhevsky, Ilya Sutskever, and Geoffrey E Hinton. “ImageNet Classification with Deep Convolutional Neural Networks”. In: Advances in Neural Information Processing Systems 25. Edited by F. Pereira et al. Curran Associates, Inc., 2012, pages 1097–1105.URL: http://papers.nips.cc/paper/4824-imagenet-classification-withdeep-convolutional-neural-networks.pdf (cited on pages 113, 185, 192, 229).

[2] Andrej Karpathy. Convolutional Networks. http://cs231n.github.io/convolutionalnetworks/ (cited on pages 186, 187, 191)

[3] Jost Tobias Springenberg et al. “Striving for Simplicity: The All Convolutional Net”. In: CoRR abs/1412.6806 (2014). URL: http://arxiv.org/abs/1412.6806 (cited on page 188).

[4] Sergey Ioffe and Christian Szegedy. “Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift”. In: CoRR abs/1502.03167 (2015). URL: http://arxiv.org/abs/1502.03167 (cited on pages 189, 193).

[5] Reddit community contributors. Batch Normalization before or after ReLU? https://www.reddit.com/r/MachineLearning/comments/67gonq/d_batch_normalization_before_or_after_relu/ (cited on page 190).