RSA

RSA

公钥加密

具有乘法同态性

程序实现

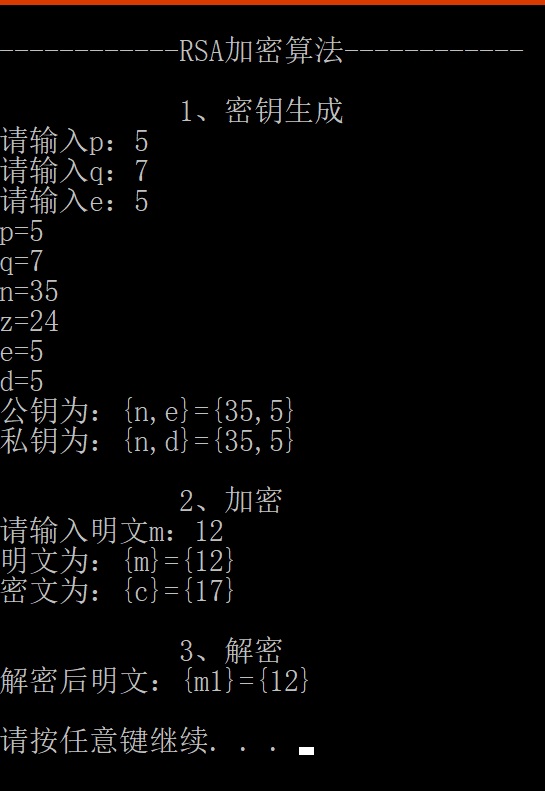
1、实现上述例子，有问题：只能是小数

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h> 
#include <time.h>
#include <math.h>
#define randomInt(a,b) (rand()%(b-a)+a)

//是否为素数
int prime(int n)
{
	int i;
	if (n < 2) {
		return -1;
	}
	else {
		for (i = 2; i < n; i++) {//判断n在2~n-1中有没有因数
			if (n % i == 0)//如果用可以除尽的数,则非素数
				break;
		}
		if (i < n) {//存在2~n-1之间有因数
			return -1;
		}
		else
			return 0;
	}
	return 0;
}
//素数生成
int creat_Prime(int a,int b)
{
	int res,k;
	srand((unsigned)time(NULL));
	do
	{
		res = randomInt(a, b);
		k = prime(res);
	} while (k == -1);
	return res;
}

//求最大公约数，判断两个数是否互素
int gcd(int x, int y)
{
	int t;
	while (y) t = x, x = y, y = t % y;
	return x;
}

//扩展欧几里得算法 （C++实现）
int exgcd(int a, int b, int& x, int& y)
{
	if (b == 0)
	{
		x = 1, y = 0;
		return a;
	}
	int ret = exgcd(b, a % b, y, x);
	y -= a / b * x;
	return ret;
}

//求逆元：基于费马定理
int reverse(int a, int mod)
{
	int x, y;
	int d = exgcd(a, mod, x, y);
	return d == 1 ? (x % mod + mod) % mod : -1;
}

//求a的b次方带模mod
int power(int a, int b, int mod)
{
	int tmp = a;
	for (int i = 0; i < b; i++)
	{
		tmp = a * tmp % mod;
	}
	return tmp % mod;
}
int main()
{
	printf("
------------RSA加密算法------------
");

	printf("
	    1、密钥生成
");
	//p和q是大素数;n=pq;z=(p-1)(q-1);任取e，使满足gcd(e,z)=1;d是e的逆;m是明文;c是密文;m1是解密后明文
	int p, q, n, z, e, d, m, c, m1;

	//随机生成p和q
	//p = creat_Prime(1, 5);
	//q = creat_Prime(5, 10);
	printf("请输入p：");
	scanf("%d", &p);
	printf("请输入q：");
	scanf("%d", &q);

	//求n和z
	n = q * p;
	z = (p - 1) * (q - 1);
	
	//随机生成e：e和z互素，e < n
	/*
	do
	{
		e = creat_Prime(1, n);
	} while (gcd(e, z) != 1);
	*/
	printf("请输入e：");
	scanf("%d", &e);
	//求d：d是e的逆元，mod z
	d = reverse(e, z);

	printf("p=%d
q=%d
n=%d
z=%d
e=%d
d=%d
", p,q,n,z,e,d);

	//输出公私钥
	printf("公钥为：{n,e}={%d,%d}
", n, e);
	printf("私钥为：{n,d}={%d,%d}
", n, d);

	printf("
	    2、加密
");
	
	//明文生成输入
	printf("请输入明文m：");
	scanf("%d",&m);

	//加密
	c = (int)pow(m, e) % n;

	printf("明文为：{m}={%d}
", m);
	printf("密文为：{c}={%d}
", c);

	printf("
	    3、解密
");
	//解密
	m1 = (int)pow(c, d) % n;

	printf("解密后明文：{m1}={%d}

", m1);

	system("pause");
	return 0;
}

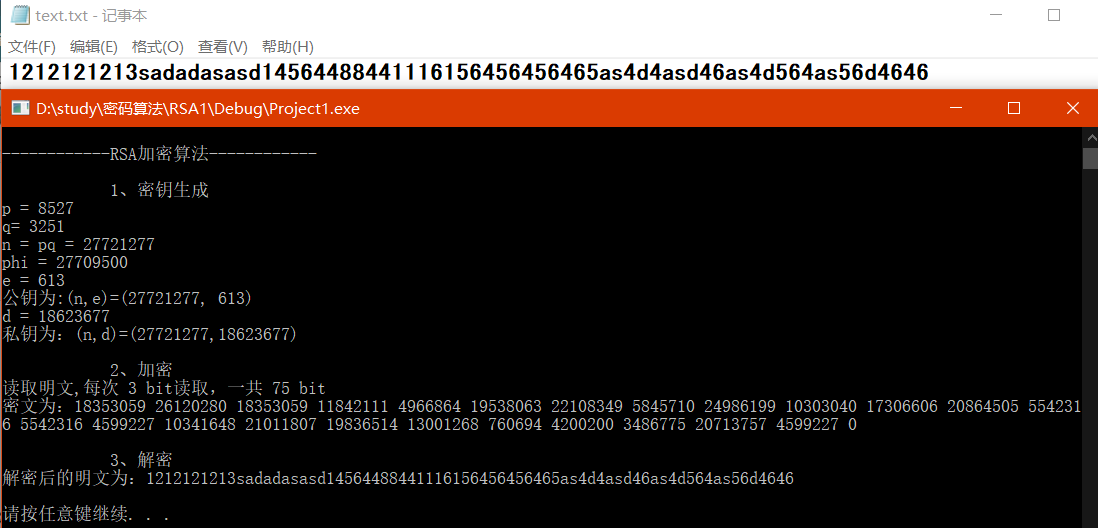
2、不使用miracl库实现大数计算，可加解密数字和字母 ，来源

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <string.h>

#define ACCURACY 5
#define SINGLE_MAX 10000
#define EXPONENT_MAX 1000
#define BUF_SIZE 1024

/**
 * Computes a^b mod c
 */
int modpow(long long a, long long b, int c) {
    int res = 1;
    while (b > 0) {
        /* Need long multiplication else this will overflow... */
        if (b & 1) {
            res = (res * a) % c;
        }
        b = b >> 1;
        a = (a * a) % c; /* Same deal here */
    }
    return res;
}

/**
 * Computes the Jacobi symbol, (a, n)
 */
int jacobi(int a, int n) {
    int twos, temp;
    int mult = 1;
    while (a > 1 && a != n) {
        a = a % n;
        if (a <= 1 || a == n) break;
        twos = 0;
        while (a % 2 == 0 && ++twos) a /= 2; /* Factor out multiples of 2 */
        if (twos > 0 && twos % 2 == 1) mult *= (n % 8 == 1 || n % 8 == 7) * 2 - 1;
        if (a <= 1 || a == n) break;
        if (n % 4 != 1 && a % 4 != 1) mult *= -1; /* Coefficient for flipping */
        temp = a;
        a = n;
        n = temp;
    }
    if (a == 0) return 0;
    else if (a == 1) return mult;
    else return 0; /* a == n => gcd(a, n) != 1 */
}

/**
 * Check whether a is a Euler witness for n
 */
int solovayPrime(int a, int n) {
    int x = jacobi(a, n);
    if (x == -1) x = n - 1;
    return x != 0 && modpow(a, (n - 1) / 2, n) == x;
}

/**
 * Test if n is probably prime, using accuracy of k (k solovay tests)
 */
int probablePrime(int n, int k) {
    if (n == 2) return 1;
    else if (n % 2 == 0 || n == 1) return 0;
    while (k-- > 0) {
        if (!solovayPrime(rand() % (n - 2) + 2, n)) return 0;
    }
    return 1;
}

/**
 * Find a random (probable) prime between 3 and n - 1, this distribution is
 * nowhere near uniform, see prime gaps
 */
int randPrime(int n) {
    int prime = rand() % n;
    n += n % 2; /* n needs to be even so modulo wrapping preserves oddness */
    prime += 1 - prime % 2;
    while (1) {
        if (probablePrime(prime, ACCURACY)) return prime;
        prime = (prime + 2) % n;
    }
}

/**
 * Compute gcd(a, b)
 */
int gcd(int a, int b) {
    int temp;
    while (b != 0) {
        temp = b;
        b = a % b;
        a = temp;
    }
    return a;
}

/**
 * Find a random exponent x between 3 and n - 1 such that gcd(x, phi) = 1,
 * this distribution is similarly nowhere near uniform
 */
int randExponent(int phi, int n) {
    int e = rand() % n;
    while (1) {
        if (gcd(e, phi) == 1) return e;
        e = (e + 1) % n;
        if (e <= 2) e = 3;
    }
}

/**
 * Compute n^-1 mod m by extended euclidian method
 */
int inverse(int n, int modulus) {
    int a = n, b = modulus;
    int x = 0, y = 1, x0 = 1, y0 = 0, q, temp;
    while (b != 0) {
        q = a / b;
        temp = a % b;
        a = b;
        b = temp;
        temp = x; x = x0 - q * x; x0 = temp;
        temp = y; y = y0 - q * y; y0 = temp;
    }
    if (x0 < 0) x0 += modulus;
    return x0;
}

/**
 * Read the file fd into an array of bytes ready for encryption.
 * The array will be padded with zeros until it divides the number of
 * bytes encrypted per block. Returns the number of bytes read.
 */
int readFile(FILE* fd, char** buffer, int bytes) {
    int len = 0, cap = BUF_SIZE, r;
    char buf[BUF_SIZE];
    *buffer = (char*)malloc(BUF_SIZE * sizeof(char));
    while ((r = fread(buf, sizeof(char), BUF_SIZE, fd)) > 0) {
        if (len + r >= cap) {
            cap *= 2;
            *buffer = (char*)realloc(*buffer, cap);
        }
        memcpy(&(*buffer)[len], buf, r);
        len += r;
    }
    /* Pad the last block with zeros to signal end of cryptogram. An additional block is added if there is no room */
    if (len + bytes - len % bytes > cap) *buffer = (char*)realloc(*buffer, len + bytes - len % bytes);
    do {
        (*buffer)[len] = '';
        len++;
    } while (len % bytes != 0);
    return len;
}

/**
 * Encode the message m using public exponent and modulus, c = m^e mod n
 */
int encode(int m, int e, int n) {
    return modpow(m, e, n);
}

/**
 * Decode cryptogram c using private exponent and public modulus, m = c^d mod n
 */
int decode(int c, int d, int n) {
    return modpow(c, d, n);
}

/**
 * Encode the message of given length, using the public key (exponent, modulus)
 * The resulting array will be of size len/bytes, each index being the encryption
 * of "bytes" consecutive characters, given by m = (m1 + m2*128 + m3*128^2 + ..),
 * encoded = m^exponent mod modulus
 */
int* encodeMessage(int len, int bytes, char* message, int exponent, int modulus) {
    int* encoded = (int*)malloc((len / bytes) * sizeof(int));
    int x, i, j;
    for (i = 0; i < len; i += bytes) {
        x = 0;
        for (j = 0; j < bytes; j++) 
            x += message[i + j] * (1 << (7 * j));
        encoded[i / bytes] = encode(x, exponent, modulus);
#ifndef MEASURE
        printf("%d ", encoded[i / bytes]);
#endif
    }
    return encoded;
}

/**
 * Decode the cryptogram of given length, using the private key (exponent, modulus)
 * Each encrypted packet should represent "bytes" characters as per encodeMessage.
 * The returned message will be of size len * bytes.
 */
int* decodeMessage(int len, int bytes, int* cryptogram, int exponent, int modulus) {
    int* decoded = (int*)malloc(len * bytes * sizeof(int));
    int x, i, j;
    for (i = 0; i < len; i++) {
        x = decode(cryptogram[i], exponent, modulus);
        for (j = 0; j < bytes; j++) {
            decoded[i * bytes + j] = (x >> (7 * j)) % 128;
#ifndef MEASURE
            if (decoded[i * bytes + j] != '') printf("%c", decoded[i * bytes + j]);
#endif
        }
    }
    return decoded;
}

/**
 * Main method to demostrate the system. Sets up primes p, q, and proceeds to encode and
 * decode the message given in "text.txt"
 */
int main(void) {
    int p, q, n, phi, e, d, bytes, len;
    int* encoded, * decoded;
    char* buffer;
    FILE* f;
    char str[600];
    srand(time(NULL));
    printf("
------------RSA加密算法------------
");
    printf("
	    1、密钥生成
");
    while (1) {
        p = randPrime(SINGLE_MAX);
        printf("p = %d
", p);

        q = randPrime(SINGLE_MAX);
        printf("q= %d
", q);

        n = p * q;
        printf("n = pq = %d
", n);
        if (n < 128) {
            printf("模数小于128,无法编码单个字节,再试一次
");
        }
        else break;
    }
    if (n >> 21) bytes = 3;
    else if (n >> 14) bytes = 2;
    else bytes = 1;

    phi = (p - 1) * (q - 1);
    printf("phi = %d
", phi);

    e = randExponent(phi, EXPONENT_MAX);
    printf("e = %d
公钥为:(n,e)=(%d, %d)

", e, n, e);

    d = inverse(e, phi);
    printf("d = %d
私钥为：(n,d)=(%d,%d)", d, n, d);

    printf("
	    2、加密
");
    printf("读取明文,");
    f = fopen("text.txt", "r");
    if (f == NULL) {
        printf("打开文件失败！是否存在?
");
        return EXIT_FAILURE;
    }
    len = readFile(f, &buffer, bytes); /* len will be a multiple of bytes, to send whole chunks */
    fclose(f);

    printf("每次 %d bit读取，一共 %d bit
密文为：",bytes,len);
    encoded = encodeMessage(len, bytes, buffer, e, n);

    printf("

	    3、解密
解密后的明文为：");
    decoded = decodeMessage(len / bytes, bytes, encoded, d, n);

    printf("

");
    free(encoded);
    free(decoded);
    free(buffer);
    system("pause");
    return EXIT_SUCCESS;
}

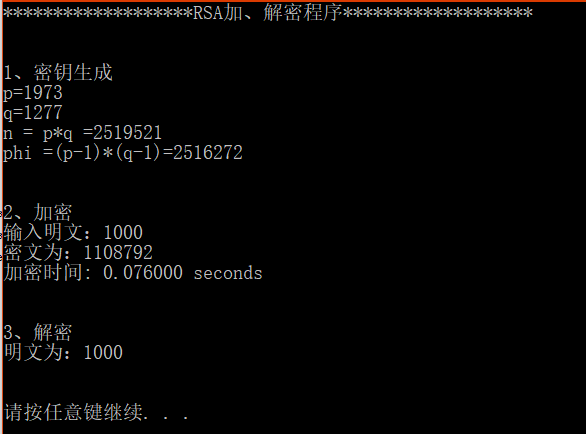
 3、使用大数库miracl，加密1000次

#include <stdio.h>
#include "miracl.h"
#include <time.h>
//char *primetext="155315526351482395991155996351231807220169644828378937433223838972232518351958838087073321845624756550146945246003790108045940383194773439496051917019892370102341378990113959561895891019716873290512815434724157588460613638202017020672756091067223336194394910765309830876066246480156617492164140095427773547319";
char *text="";
time_t begin, end;

int main()
{
	/*
		加解密
	*/
    big a,b,p,q,n,p1,q1,phi,pa,pb,key,e,d,dp,dq,t,m,c;
    big primes[2],pm[2];
    big_chinese ch;
	long l=12;
	long cum=0;
    miracl *mip;
	char input[256];
#ifndef MR_NOFULLWIDTH   
    mip=mirsys(100,0);
#else
    mip=mirsys(100,MAXBASE);
#endif
    a=mirvar(0);
    b=mirvar(0);
    p=mirvar(0);
    q=mirvar(0);
    n=mirvar(0);
    p1=mirvar(0);
    q1=mirvar(0);
    phi=mirvar(0);
    pa=mirvar(0);
    pb=mirvar(0);
    e=mirvar(0);
    d=mirvar(0);
    dp=mirvar(0);
    dq=mirvar(0);
    t=mirvar(0);
    m=mirvar(0);
    c=mirvar(0);
    pm[0]=mirvar(0);
    pm[1]=mirvar(0);
	printf("*******************RSA加、解密程序*******************

");

    printf("
1、密钥生成
");
    do 
    {
        bigbits(l,p);
        if (subdivisible(p,2)) incr(p,1,p);
        while (!isprime(p)) incr(p,2,p);

        bigbits(l,q);
        if (subdivisible(q,2)) incr(q,1,q);
        while (!isprime(q)) incr(q,2,q);

        multiply(p,q,n);      /* n=p.q */

        lgconv(65537L,e);
        decr(p,1,p1);
        decr(q,1,q1);
        multiply(p1,q1,phi);  /* phi =(p-1)*(q-1) */
    } while (xgcd(e,phi,d,d,t)!=1);
	printf("p=");
    cotnum(p,stdout);
	printf("q=");
    cotnum(q,stdout);
    printf("n = p*q =");
    cotnum(n,stdout);
	printf("phi =(p-1)*(q-1)=");
    cotnum(phi,stdout);

/* set up for chinese remainder thereom */
    primes[0]=p;
    primes[1]=q;
    crt_init(&ch,2,primes);
    copy(d,dp);
    copy(d,dq);
    divide(dp,p1,p1);   /* dp=d mod p-1 */
    divide(dq,q1,q1);   /* dq=d mod q-1 */
    

    printf("

2、加密
");
	printf("输入明文：");
	scanf("%s",input);
	text=input;
	mip->IOBASE=l;
    cinstr(m,text);
    mip->IOBASE=10;
	begin = clock();
	while(cum<10000)
	{
	    powmod(m,e,n,c);
		cum++;
	}
    printf("密文为：");
    cotnum(c,stdout);
	end = clock();
	printf("加密时间: %f seconds
", (double)(end - begin) / CLOCKS_PER_SEC);
    zero(m);

    printf("

3、解密
");

    powmod(c,dp,p,pm[0]);    /* get result mod p */
    powmod(c,dq,q,pm[1]);    /* get result mod q */
    crt(&ch,pm,m);           /* combine them using CRT */

    printf("明文为：");
    mip->IOBASE=l;
    cotnum(m,stdout);
    crt_end(&ch);
	printf("

");
	system("pause");
    return 0;

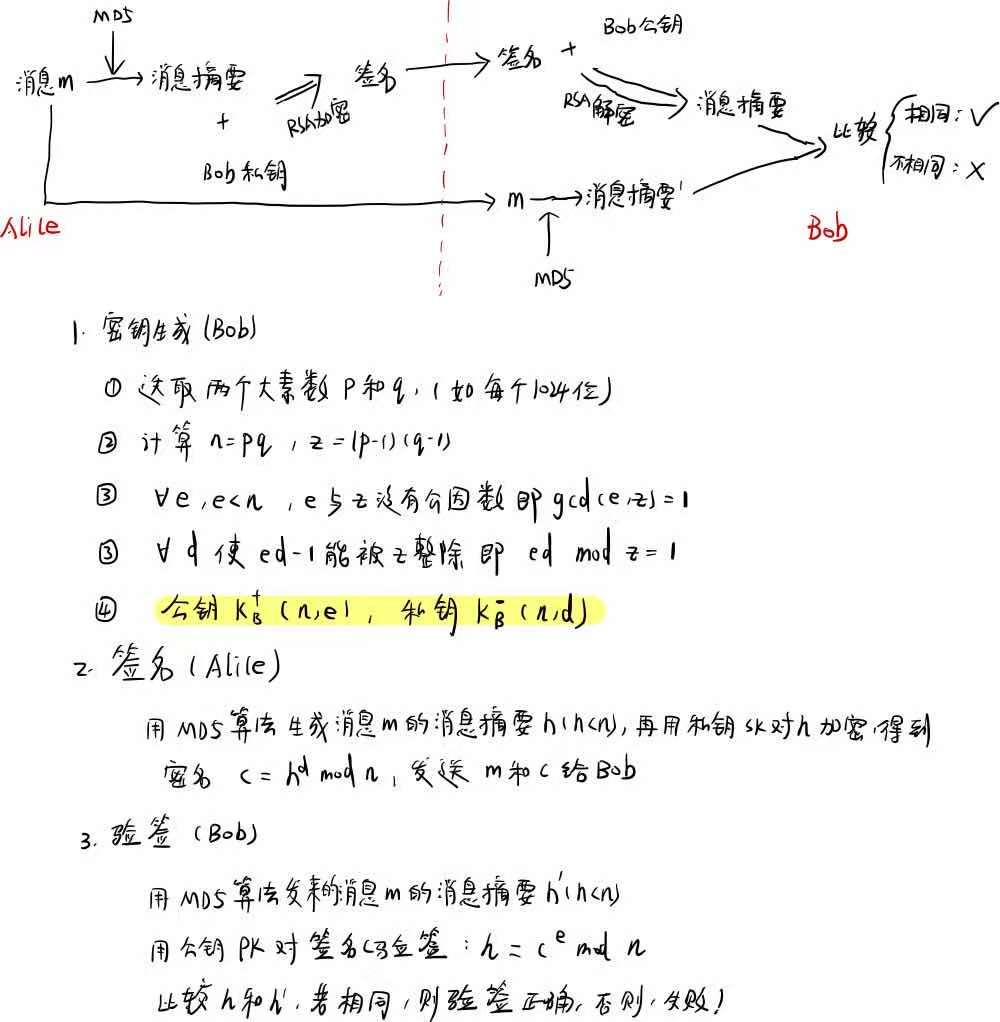
数字签名

参考

1、初探全同态加密：FHE的定义与历史回顾

2、密码基础

3、基于同态加密的金融数据安全共享方案研究及实现-王婧琳

4、RSA 小规模演算