
介绍
在机器学习算法的世界里,特征工程是非常重要的。实际上,作为一名数据科学家,这是我最喜欢的方面之一!从现有特征中设计新特征并改进模型的性能,这就是我们进行最多实验的地方。
世界上一些顶级数据科学家依靠特征工程来提高他们在竞赛排行榜得分。我相信你甚至会在结构化数据上使用各种特征工程技术。
我们可以将此技术扩展到非结构化数据(例如图像)吗?对于计算机视觉爱好者来说,这是一个有趣的问题,我们将在本文中解决这个问题。准备好对图像数据进行特征提取形式的特征工程吧!
在本文中,我将向你介绍一种流行的图像特征提取技术——方向梯度直方图(Histogram of Oriented Gradients),或俗称的HOG。我们将了解什么是HOG特征描述子,它是如何工作的(算法背后的完整数学原理),最后,用Python实现它。
目录
- 什么是特征描述子?
- HOG特征描述子简介
- HOG的计算过程
- 预处理数据
- 计算梯度
- 计算幅值和方向
- 使用梯度和方向创建直方图的方法
- HOG的计算过程
- 计算梯度直方图
- 标准化梯度
- 一幅完整图像的特征
- 在Python中实现HOG特征描述子
什么是特征描述子?
你可能在阅读标题时就已经遇到了这个问题。所以,在我们跳进文章的HOG部分之前,首先要清楚这一点。
看看下面显示的两个图像。你能分辨出图像中的物体吗?

我们可以清楚地看到这里的右图有狗,左图有车。现在,让我让这项任务稍微复杂一点,分辨下图所示的对象:

还是挺容易的。你能猜出第一种和第二种情况之间有什么区别吗?第一对图像有很多信息,比如物体的形状,颜色,边缘,背景等。
另一方面,第二对信息少得多(只有形状和边缘),但它仍然足以区分这两个图像。
你知道我想说什么吗?在第二种情况下,我们还是很容易区分对象,因为它具有识别对象所需的必要信息。这正是特征描述子的作用:
它是图像的简化表示,仅包含有关图像的最重要信息。
以下是一些最受欢迎的的特征描述子。
- HOG:方向梯度直方图
- SIFT:尺度不变的特征变换
- SURF:加速稳健特征
在本文中,我们将重点关注HOG特征描述子及其工作原理。让我们开始吧!
HOG特征描述子简介
HOG(Histogram of Oriented Gradients)是一种特征描述子,通常用于从图像数据中提取特征。它广泛用于计算机视觉任务的物体检测。
让我们看一下HOG的一些重要方面,它们与其他特征描述子不同:
- HOG描述符关注对象的结构或形状。现在你可能会问,这和我们为图像提取的边缘特征有什么不同?在边缘特征的情况下,我们只识别像素是否是边缘。HOG还能够提供边缘方向。这是通过提取边缘的梯度和方向(或者你可以说大小和方向)来实现的
- 此外,这些方向是在“局部”进行部分计算的。这意味着整个图像被分割成更小的区域,对于每个区域,计算梯度和方向。我们将在接下来的小节中更详细地讨论这个问题
- 最后,HOG将分别为这些区域生成一个直方图。直方图是使用像素值的梯度和方向创建的,因此得名“方向梯度直方图”。
给一个正式定义:
HOG特征描述子计算图像局部区域中梯度方向的出现次数。
使用OpenCV等工具实现HOG非常简单。这只是几行代码,因为我们在skimage.feature库中有一个名为hog的预定义函数。但是,我们在本文中的重点是如何实际计算这些特征。
计算方向梯度直方图(HOG)的过程
我们现在应该对HOG特征描述子的基本概念有所了解。是时候深入研究本文背后的核心思想了。让我们讨论HOG的逐步计算过程。
考虑下面的尺寸图像(180 x 280)。让我们详细了解如何为此图像创建HOG特征:

第一步:预处理数据(64x128)
这是大多数人都非常熟悉的一步。预处理数据是任何机器学习项目中的关键步骤,即使在处理图像时也没有什么不同。
我们需要对图像进行预处理,并将宽高比降低到1:2。图像大小最好是64 x 128。这是因为我们将图像分成88和1616小块来提取特征。具有指定的大小(64 x 128)将使我们的所有计算相当简单。事实上,这正是原始论文中使用的值。
回到我们的例子,让我们将大小为64x128作为目前的标准图像大小。以下是调整后的图像:

第二步:计算梯度(x和y方向)
下一步是计算图像中每个像素的梯度。梯度是x和y方向上的小变化。这里,我要从图像中取一小块,然后计算它的梯度:
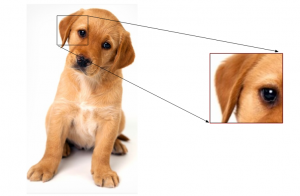
我们将得到这个部分的像素值。假设我们为给定的部分生成下面的像素矩阵(这里的矩阵只是作为一个例子,这些并不是给定部分的原始像素值):

我突出显示了像素值85。现在,要确定x方向上的梯度,我们需要从右边的像素值减去左边的值。类似地,为了计算y方向的梯度,我们将从所选像素上的像素值减去下面的像素值。
因此,该像素的x和y方向的梯度为:
- X方向的变化($G_x$)= 89-78 = 11
- Y方向的变化($G_y$)= 68-56 = 8
这个过程将给我们两个新的矩阵,一个在x方向上存储梯度,另一个在y方向上存储梯度。这类似于使用大小为1的Sobel内核。当发生剧烈变化时(例如在边缘附近),幅值(magnitude)会更高。
我们分别计算了x和y方向的梯度。对图像中的所有像素重复相同的过程。下一步是使用这些值找到幅值和方向。
第三步:计算幅值和方向
使用我们在最后一步中计算的梯度,我们现在将确定每个像素值的大小和方向。对于这一步,我们将使用勾股定理(是的,与你在学校学习的那个相同!)。
看看下面的图片:

在之前的例子中,Gx和Gy分别是11和8。应用勾股定理计算总梯度大小:
- 总梯度幅值=$√[(G_x)^2 (G_y)^2]$
- 总梯度幅值=$√[(11)^2 (8)^2]= 13.6$
接下来,计算相同像素的方向。我们知道我们可以把角度写成tan
$$tan(Φ)= Gy/Gx$$
因此,角度的值将是:
$$Φ= atan(Gy/Gx)$$
当我们代入这些值时,角度是36°。现在,对于每个像素值,我们有总梯度(幅值)和方向。我们需要使用这些梯度和方向生成直方图。
但是请稍等——在深入研究HOG特征描述子中如何创建直方图之前,我们需要稍作休息。把这看作是整个过程中的一小步。我们将首先讨论一些简单的方法来创建直方图使用两个值,梯度和方向。
使用梯度和方向创建直方图的不同方法
直方图是显示一组连续数据的频率分布的图。变量(以箱子的形式)在x轴上,频率在y轴上。这里,我们设x轴上为角度,y轴为频率。
方法1:
让我们从生成直方图的最简单方法开始。我们将取每个像素值,找到像素的方向并更新频率表。
下面是高亮像素(85)的处理过程。由于该像素的角度为36°,我们将对角度值36添加一个数字,表示频率:

对所有像素值重复相同的过程,最后得到一个频率表,表示角度以及这些角度在图像中的出现情况。这个频率表可用于生成在x轴上有角度值的直方图和在y轴上有频率值的直方图。
这是创建直方图的一种方法。注意,这里直方图的bin值(角度的间隔)为1。因此我们得到大约180个不同的桶,每个桶代表一个角度值。另一种方法是为更大的角度值间隔创建直方图特征。
方法2:
这个方法与前面的方法类似,不同之处在于我们的bin值为20。因此,我们在这里得到的桶数是9。
同样,对于每个像素,我们将检查角度,并以9 x 1矩阵的形式存储角度值的频率。绘制这个将给我们直方图:

方法3:
上述两种方法仅使用角度值来生成直方图,并且不考虑梯度值。这是我们可以生成直方图的另一种方式 - 我们可以使用梯度幅值(magnitude)来填充矩阵中的值,而不是使用频率。以下是示例:

方法4:
让我们对上面的方法做一个小修改。在这里,我们将像素梯度的贡献添加到像素梯度两侧的区间。请记住,更接近角度的bin值有更高的贡献。

这正是在HOG特征描述子中创建直方图的方式。
第4步:计算8×8单元(9×1)中梯度的直方图
HOG特征描述子中创建的直方图不会为整个图像生成。将图像分割为8×8个单元格,计算每个单元格的方向梯度直方图。
通过这样做,我们得到了代表整个图像的小块的特征(或直方图)。我们当然可以把这个值从8 x 8换成16 x 16或者32 x 32。
如果我们将图像划分为8×8个单元格并生成直方图,我们使用我们在上一节中讨论的方法4生成该矩阵,将为每个单元格获得9 x 1矩阵。

一旦我们为图像中的8×8小块生成了HOG,下一步就是对直方图进行标准化。
步骤5:将16×16单元(36×1)中的梯度标准化
在我们理解这是如何做到的之前,首先理解为什么要这样做是很重要的。
虽然我们已经为图像的8×8单元创建了HOG特征,但是图像的梯度对整体光照很敏感。这意味着对于特定的图像,图像的某些部分与其他部分相比会非常明亮。
我们不能从图像中完全消除这个。但是我们可以通过使用16×16个块来对梯度进行归一化来减少这种光照变化。下面的例子可以解释如何创建16×16块:

在这里,我们将组合四个8×8单元来创建一个16×16块。并且我们已经知道每个8×8单元具有用于直方图的9×1矩阵。因此,我们将有四个9×1矩阵或一个36×1矩阵。为了标准化该矩阵,我们将这些值中的每一个除以值的平方和的平方根。在数学上,对于给定的向量V:
$$V = [a1,a2,a3,... a36]$$
我们计算平方和的根:
$$k =√(a1)2 (a2)2 (a3)2 .... (A36)2$$
并将向量V中的所有值除以此值k:
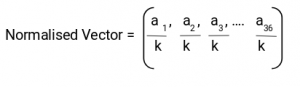
结果将是尺寸为36×1的归一化向量。
第6步:完整图像的特征
我们现在正处于为图像生成HOG特征的最后一步。到目前为止,我们已经为16×16块图像创建了特征。现在,我们将结合所有这些来获得最终图像的特征。
你能猜出我们将为给定图像提供的特征总数是多少?我们首先需要找出一个64×128图像可以得到多少这样的16×16块:

我们将有105(7×15)块16×16。这105个块中的每一个都具有36×1的向量作为特征。因此,图像的总特征将是105×36×1 = 3780个特征。
我们现在将为单个图像生成HOG特征,并验证我们是否在最后获得相同数量的特征。
在Python中实现HOG特征描述子
是时候实现了!我敢肯定,这是本文中最受期待的部分。让我们开始吧。
我们将看到如何在单个图像上生成HOG特征,以及是否可以在更大的数据集上应用相同的HOG特征。我们将首先加载所需的库和我们要为其创建HOG特征的图像:
#导入所需的库
from skimage.io import imread, imshow
from skimage.transform import resize
from skimage.feature import hog
from skimage import exposure
import matplotlib.pyplot as plt
%matplotlib inline
#读入图片
img = imread('puppy.jpeg')
imshow(img)
print(img.shape)(663,459,3)
我们可以看到图像的形状是663 x 459.我们将不得不将此图像调整为64 x 128.请注意,我们使用的是skimage,它将输入作为高度x宽度。
#调整图像大小
resized_img = resize(img, (128,64))
imshow(resized_img)
print(resized_img.shape)(128,64,3)
在这里,我将直接使用skimage.features的hog函数。因此,我们不必单独计算梯度,幅值(总梯度)和方向。hog函数将在内部计算它并返回特征矩阵。
此外,如果你设置参数'visualize = True',它将返回HOG的图像。
#创建hog特征
fd, hog_image = hog(resized_img, orientations=9, pixels_per_cell=(8, 8),
cells_per_block=(2, 2), visualize=True, multichannel=True)在继续之前,让我先介绍一下这些超参数代表什么。或者,你可以在此处查看官方文档中的定义。
- orientations是我们要创建桶的数量。由于我想要一个9 x 1矩阵,我将orientations设置为9
- pixelspercell定义我们为其创建直方图的单元格的大小。在我们在本文中介绍的示例中,我们使用了8 x 8个单元格,在这里我将设置相同的值。如前所述,你可以选择更改此值
- 我们有另一个超参数cellperblock,它是我们对直方图进行标准化的块的大小。这个参数是每个块的单元格数量而不是像素的数量。因此,我们将使用2 x 2而不是16 x 16
函数的特征矩阵存储在变量fd中,图像存储在hog_image中。让我们检查一下特征矩阵的形状:
fd.shape(3780)'''
HOG FEATURES
'''
# 导入需要的包
from skimage.io import imread, imshow
from skimage.transform import resize
from skimage.feature import hog
from skimage import exposure
#读取图片
img = imread('puppy.jpeg')
#改变图片尺寸
resized_img = resize(img, (128,64))
#产生HOG特征
fd, hog_image = hog(resized_img, orientations=9, pixels_per_cell=(8, 8),
cells_per_block=(2, 2), visualize=True, multichannel=True)
print('
Shape of Image Features
')
print(fd.shape)Shape of Image Features
(3780,)正如预期的那样,我们有3,780个图像特征,这验证了我们之前在步骤7中所做的计算。你可以选择更改超参数的值,这将为你提供不同大小的特征矩阵。
让我们最后看看HOG图像:
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 8), sharex=True, sharey=True)
ax1.imshow(resized_img, cmap=plt.cm.gray)
ax1.set_title('Input image')
# 缩放直方图以便更好地显示
hog_image_rescaled = exposure.rescale_intensity(hog_image, in_range=(0, 10))
ax2.imshow(hog_image_rescaled, cmap=plt.cm.gray)
ax2.set_title('Histogram of Oriented Gradients')
plt.show()
结束笔记
本文背后的想法是让你了解HOG特征描述子背后的实际原理以及如何计算特征。整个过程分为7个简单步骤。
下一步,我鼓励你尝试在简单的计算机视觉问题上使用HOG特征,并查看模型性能是否有所改善。
欢迎关注磐创博客资源汇总站:http://docs.panchuang.net/
欢迎关注PyTorch官方中文教程站:http://pytorch.panchuang.net/