二叉树

目录

• 一：术语、定义、特点
  • 1、树
    • 树结构中的术语
  • 2、二叉树
    • 二叉树结构特点
    • 二叉树性质
    • 考试时常考性质4的证明
  • 3、几种特殊形态的二叉树
    • 3.1 满二叉树
    • 3.2 完全二叉树
    • 3.3 平衡二叉树
    • 3.4 二叉搜索树
• 二：二叉树的代码实现
  • 1、创建节点
  • 2、递归实现二叉树的三序遍历
    • 2.1 前序遍历
    • 2.2 中序遍历
    • 2.3 后序遍历
  • 3、层序遍历
  • 4、求二叉树中的节点数
  • 5、求二叉树的深度
  • 6、判断二叉树是否是平衡二叉树
  • 7、判断两棵二叉树结构是否相同
  • 8、求二叉树第k层节点个数
  • 9、求二叉树的叶子节点个数
  • 10、求二叉树的镜像
  • 11、求二叉树中两个节点的最近公共祖先节点
    • 递归思路
    • 非递归思路
  • 12、判断二叉树是否为完全二叉树

一：术语、定义、特点

1、树

树是一种数据结构，它是由n（n>=1）个有限结点组成一个具有层次关系的集合。

树结构中的术语

1. 节点的度：节点拥有的子树的数目；
2. 叶子节点：度为0的节点；
3. 分支结点：度不为0的节点；
4. 树的度：树中节点的最大的度；
5. 层次：根结点的层次为1，其余节点的层次等于该结点的双亲节点的层次加1；
6. 树的高度：树中节点的最大层次；
7. 森林：0个或多个不相交的树组成。对森林加上一个根，森林即成为树；删去根，树即成为森林。

2、二叉树

二叉树也是树；
二叉树有五种基本形态，如下图：

二叉树结构特点

1. 每个节点最多有两个子树（即二叉树的度不能大于2），并且二叉树的子树有左右之分，其次序不能颠倒；
2. 没有父节点的节点称为根节点；
3. 没有子节点的节点称为叶子节点；
4. 每一个非根节点有且只有一个父节点；
5. 除了根节点外，每个子节点可以分为多个不相交的子树；
6. 树里面没有环路。

二叉树性质

性质1：在二叉树的第 i 层上最多有 2^(i – 1) 个节点； (i>=1)
性质2：深度为 k 的二叉树至多有 2^k – 1 个节点；(k>=1)
性质3：包含n个节点的二叉树的高度至少为(log2n)+1；
性质4：在任意一棵二叉树中，若终端节点的个数为n0，度为2的节点数为n2，则n0=n2+1；

考试时常考性质4的证明

性质4：在任意一棵二叉树中，若终端节点的个数为n0，度为2的节点数为n2，则n0=n2+1。
证明：因为二叉树中所有节点的度数均不大于2，不妨设n0表示度为0的节点个数，n1表示度为1的节点个数，n2表示度为2的节点个数。三类节点加起来为总结点个数，于是便可得到：n=n0+n1+n2 (式1)
由度之间的关系可得第二个等式：n=n00+n11+n2*2+1即n=n1+2n2+1 (式2)
合（式1）（式2），移项可得：n0=n2+1，证毕。

3、几种特殊形态的二叉树

3.1 满二叉树

深度为k 且有2^k -1 个节点的二叉树。

∴
已知某二叉树深度为k,则该树最多有2^k - 1个节点；

每层有2^k+1 个节点；

3.2 完全二叉树

深度为k，有n个节点的二叉树，其每一个节点都与深度为k 的满二叉树中编号从1 至n 的节点一一对应。

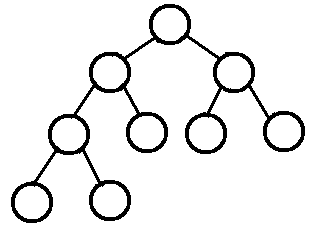
特点：叶子节点只能出现在最下层和次下层，且最下层的叶子节点集中在树的左部。显然，一棵满二叉树必定是一棵完全二叉树，而完全二叉树未必是满二叉树。

面试题：如果一个完全二叉树的节点总数为768个，求叶子节点的个数。
由二叉树的性质知：n0=n2+1，将之带入768=n0+n1+n2中得：768=n1+2n2+1，因为完全二叉树度为1的节点个数要么为0，要么为1，那么就把n1=0或者1都代入公式中，很容易发现n1=1才符合条件。所以算出来n2=383，所以叶子节点个数n0=n2+1=384。

总结：如果一棵完全二叉树的节点总数为n，那么叶子节点等于n/2（当n为偶数时）或者(n+1)/2（当n为奇数时）

3.3 平衡二叉树

当且仅当两个子树的高度差不超过1时，这个树是平衡二叉树。

3.4 二叉搜索树

又称二叉查找树，设x为二叉查找树中的一个节点，x节点包含关键字key，节点x的key值计为key[x]。如果y是x的左子树中的一个节点，则key[y]<=key[x]；如果y是x的右子树的一个节点，则key[y]>=key[x]。即满足：左子树<=根节点<=右子树。

（1）若任意节点的左子树不空，则左子树上所有节点的值均小于它的根节点的值。

（2）任意节点的右子树不空，则右子树上所有节点的值均大于它的根节点的值。

（3）任意节点的左、右子树也分别为二叉查找树。

二：二叉树的代码实现

typedef struct node{
    type_t data;
    struct node *left;
    struct node *right;
}Node;

1、创建节点

Node *node_create(type_t data){
    Node *p = (Node *)malloc(sizeof(Node));
    p->data = data;
    p->left = NULL;
    p->right = NULL;
    return p;
}

2、递归实现二叉树的三序遍历

2.1 前序遍历

void tree_pre_order(Node *tree){
    if(tree == NULL)
        return;
    else{
        printf("pre: %d
", tree->data);
        tree_pre_order(tree->left);
        tree_pre_order(tree->right);
    }
}

2.2 中序遍历

void tree_in_order(Node *tree){
    if(tree == NULL)
        return;
    else{
        tree_in_order(tree->left);
        printf("in: %d
", tree->data);
        tree_in_order(tree->right);
    }
}

2.3 后序遍历

void tree_post_order(Node *tree){
    if(tree == NULL)
        return;
    else{
        tree_post_order(tree->left);
        tree_post_order(tree->right);
        printf("next: %d
", tree->data);
    }
}

3、层序遍历

思路：相当于广度优先搜索，使用队列实现。队列初始化，将根节点压入队列。当队列不为空，进行如下操作：弹出一个节点，访问，若左子节点或右子节点不为空，将其压入队列。

void LevelTraverse(BinaryTreeNode * pRoot){
	if(pRoot == NULL)
		return;
	queue<BinaryTreeNode *> q;
	q.push(pRoot);
	while(!q.empty()){
		BinaryTreeNode * pNode = q.front();
		q.pop();
		Visit(pNode); // 访问节点
		if(pNode->m_pLeft != NULL)
			q.push(pNode->m_pLeft);
		if(pNode->m_pRight != NULL)
			q.push(pNode->m_pRight);
	}
	return;
}

4、求二叉树中的节点数

递归思路：

（1）如果二叉树为空，节点个数为0；

（2）如果二叉树不为空，二叉树节点个数 = 左子树节点个数 + 右子树节点个数 + 1；

int GetNodeNum(BinaryTreeNode * pRoot){
	// 递归出口
	if(pRoot == NULL) 
		return 0;
	return GetNodeNum(pRoot->m_pLeft) + GetNodeNum(pRoot->m_pRight) + 1;
}

5、求二叉树的深度

递归思路：

（1）如果二叉树为空，二叉树的深度为0；

（2）如果二叉树不为空，二叉树的深度 = max(左子树深度， 右子树深度) + 1；

int GetDepth(BinaryTreeNode * pRoot){
	// 递归出口
	if(pRoot == NULL) 
		return 0;
	int depthLeft = GetDepth(pRoot->m_pLeft);
	int depthRight = GetDepth(pRoot->m_pRight);
	return depthLeft > depthRight ? (depthLeft + 1) : (depthRight + 1); 
}

python版：

def treeDepth(self,root):
	if not root:
		return 0
	depthLeft = self.treeDepth(root.left)
	depthRight = self.treeDepth(root.right)
return depthLeft+1 if depthLeft > depthRight else depthRight+1

6、判断二叉树是否是平衡二叉树

递归思路：

（1）如果二叉树为空，返回真；

（2）如果二叉树不为空，如果左子树和右子树都是AVL树并且左子树和右子树高度相差不大于1，返回真，其他返回假；

bool IsAVL(BinaryTreeNode * pRoot, int & height){
	// 空树，返回真
	if(pRoot == NULL) {
		height = 0;
		return true;
	}
	int heightLeft;
	bool resultLeft = IsAVL(pRoot->m_pLeft, heightLeft);
	int heightRight;
	bool resultRight = IsAVL(pRoot->m_pRight, heightRight);
	// 左子树和右子树都是AVL，并且高度相差不大于1，返回真
	if(resultLeft && resultRight && abs(heightLeft - heightRight) <= 1) {
		height = max(heightLeft, heightRight) + 1;
		return true;
	}
	else{
		height = max(heightLeft, heightRight) + 1;
		return false;
	}
}

python版：

# 判断平衡二叉树
def isBalanced(self,root):
	"""
	:typeroot:TreeNode
	:rtype:bool
	"""
	if not root:
		return True
	resultLeft = self.isBalanced(root.left)
	heightLeft = self.treeDepth(root.left)
	resultRight = self.isBalanced(root.right)
	heightRight = self.treeDepth(root.right)
	#左子树和右子树都是AVL，并且高度相差不大于1，返回真
	if resultLeft and resultRight and abs(heightLeft-heightRight) <= 1:
		return True
	else:
		return False

#求二叉树的深度
def treeDepth(self,root):
	if not root:
		return 0
	depthLeft = self.treeDepth(root.left)
	depthRight = self.treeDepth(root.right)
return depthLeft + 1 if depthLeft > depthRight else depthRight + 1

7、判断两棵二叉树结构是否相同

不考虑数据内容。结构相同意味着对应的左子树和对应的右子树都结构相同。

递归思路：

（1）如果两棵二叉树都为空，返回真；

（2）如果两棵二叉树一棵为空，另一棵不为空，返回假；

（3）如果两棵二叉树都不为空，如果对应的左子树和右子树都同构返回真，其他返回假；

bool StructureCmp(BinaryTreeNode * pRoot1, BinaryTreeNode * pRoot2){
	// 都为空，返回真
	if(pRoot1 == NULL && pRoot2 == NULL) 
		return true;
	// 有一个为空，一个不为空，返回假
	else if(pRoot1 == NULL || pRoot2 == NULL) 
		return false;
	// 比较对应左子树
	bool resultLeft = StructureCmp(pRoot1->m_pLeft, pRoot2->m_pLeft);  
	bool resultRight = StructureCmp(pRoot1->m_pRight, pRoot2->m_pRight); // 比较对应右子树
	return (resultLeft && resultRight);
}

8、求二叉树第k层节点个数

递归思路：

（1）如果二叉树为空或者k<1返回0；

（2）如果二叉树不为空并且k==1，返回1；

（3）如果二叉树不为空且k>1，返回左子树中k-1层的节点个数与右子树k-1层节点个数之和；

int GetNodeNumKthLevel(BinaryTreeNode * pRoot, int k){
	if(pRoot == NULL || k < 1)
		return 0;
	if(k == 1)
		return 1;
	// 左子树中k-1层的节点个数
	int numLeft = GetNodeNumKthLevel(pRoot->m_pLeft, k-1);  
	// 右子树中k-1层的节点个数
	int numRight = GetNodeNumKthLevel(pRoot->m_pRight, k-1); 
	return (numLeft + numRight);
}

9、求二叉树的叶子节点个数

递归思路：

（1）如果二叉树为空，返回0；

（2）如果二叉树不为空且左右子树为空，返回1；

（3）如果二叉树不为空，且左右子树不同时为空，返回左子树中叶子节点个数加上右子树中叶子节点个数；

int GetLeafNodeNum(BinaryTreeNode * pRoot){
	if(pRoot == NULL)
		return 0;
	if(pRoot->m_pLeft == NULL && pRoot->m_pRight == NULL)
		return 1;
	int numLeft = GetLeafNodeNum(pRoot->m_pLeft); // 左子树中叶节点的个数
	int numRight = GetLeafNodeNum(pRoot->m_pRight); // 右子树中叶节点的个数
	return (numLeft + numRight);
}

10、求二叉树的镜像

递归思路：

（1）如果二叉树为空，返回空；

（2）如果二叉树不为空，求左子树和右子树的镜像，然后交换左子树和右子树；

BinaryTreeNode * Mirror(BinaryTreeNode * pRoot){
	if(pRoot == NULL) // 返回NULL
		return NULL;
	BinaryTreeNode * pLeft = Mirror(pRoot->m_pLeft); // 求左子树镜像
	BinaryTreeNode * pRight = Mirror(pRoot->m_pRight); // 求右子树镜像
      // 交换左子树和右子树
	pRoot->m_pLeft = pRight;
	pRoot->m_pRight = pLeft;
	return pRoot;
}

11、求二叉树中两个节点的最近公共祖先节点

递归思路

（1）如果两个节点分别在根节点的左子树和右子树，则返回根节点；

（2）如果两个节点都在左子树，则递归处理左子树；如果两个节点都在右子树，则递归处理右子树；

bool FindNode(BinaryTreeNode * pRoot, BinaryTreeNode * pNode){
	if(pRoot == NULL || pNode == NULL)
		return false;

	if(pRoot == pNode)
		return true;
 
	bool found = FindNode(pRoot->m_pLeft, pNode);
	if(!found)
		found = FindNode(pRoot->m_pRight, pNode);
	return found;
}
BinaryTreeNode * GetLastCommonParent(BinaryTreeNode * pRoot, BinaryTreeNode * pNode1,           BinaryTreeNode * pNode2){
	if(FindNode(pRoot->m_pLeft, pNode1)){
		if(FindNode(pRoot->m_pRight, pNode2))
			return pRoot;
		else
			return GetLastCommonParent(pRoot->m_pLeft, pNode1, pNode2);
	}
	else{
		if(FindNode(pRoot->m_pLeft, pNode2))
			return pRoot;
		else
			return GetLastCommonParent(pRoot->m_pRight, pNode1, pNode2);
	}
}

非递归思路

先求从根节点到两个节点的路径，然后再比较对应路径的节点就行，最后一个相同的节点也就是他们在二叉树中的最低公共祖先节点。

bool GetNodePath(BinaryTreeNode * pRoot, BinaryTreeNode * pNode, 
                 list<BinaryTreeNode *> & path){
	if(pRoot == NULL)
		return false;
    if(pRoot == pNode){	
		path.push_back(pRoot);
		return true;
	}
	path.push_back(pRoot);
	bool found = false;
	found = GetNodePath(pRoot->m_pLeft, pNode, path);
	if(!found)
		found = GetNodePath(pRoot->m_pRight, pNode, path);
	if(!found)
		path.pop_back();
	return found;
}
BinaryTreeNode * GetLastCommonParent(BinaryTreeNode * pRoot, BinaryTreeNode * pNode1, BinaryTreeNode * pNode2){
	if(pRoot == NULL || pNode1 == NULL || pNode2 == NULL)
		return NULL;
	list<BinaryTreeNode*> path1;
	bool bResult1 = GetNodePath(pRoot, pNode1, path1);
	list<BinaryTreeNode*> path2;
	bool bResult2 = GetNodePath(pRoot, pNode2, path2);
	if(!bResult1 || !bResult2) 
		return NULL;
	BinaryTreeNode * pLast = NULL;
	list<BinaryTreeNode*>::const_iterator iter1 = path1.begin();
	list<BinaryTreeNode*>::const_iterator iter2 = path2.begin();
	while(iter1 != path1.end() && iter2 != path2.end()){
		if(*iter1 == *iter2)
			pLast = *iter1;
		else
			break;
		iter1++;
		iter2++;
	}
	return pLast;
}

12、判断二叉树是否为完全二叉树

首先考虑完全二叉树的特点：若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。

可得思路：按层次（从上到下，从左到右）遍历二叉树，当遇到一个节点的左子树为空时，则该节点右子树必须为空，且后面遍历的节点左右子树都必须为空，否则不是完全二叉树。

bool IsCompleteBinaryTree(BinaryTreeNode * pRoot){
	if(pRoot == NULL)
		return false;
	queue<BinaryTreeNode *> q;
	q.push(pRoot);
	bool mustHaveNoChild = false;
	bool result = true;
	while(!q.empty()){
		BinaryTreeNode * pNode = q.front();
		q.pop();
		 // 已经出现了有空子树的节点了，后面出现的必须为叶节点（左右子树都为空）
		if(mustHaveNoChild){
			if(pNode->m_pLeft != NULL || pNode->m_pRight != NULL){
				result = false;
				break;
			}
		}
		else{
			if(pNode->m_pLeft != NULL && pNode->m_pRight != NULL){
				q.push(pNode->m_pLeft);
				q.push(pNode->m_pRight);
			}
			else if(pNode->m_pLeft != NULL && pNode->m_pRight == NULL){
				mustHaveNoChild = true;
				q.push(pNode->m_pLeft);
			}
			else if(pNode->m_pLeft == NULL && pNode->m_pRight != NULL){
				result = false;
				break;
			}
			else{
				mustHaveNoChild = true;
			}
		}
	}
	return result;
}