Genesis 多边形闭轮廓填充算法

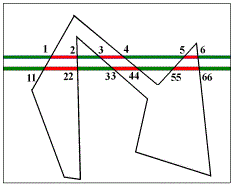
 通过逐行扫描，计算得出直线与多边形相交点进行求解

原理图形如下所示：

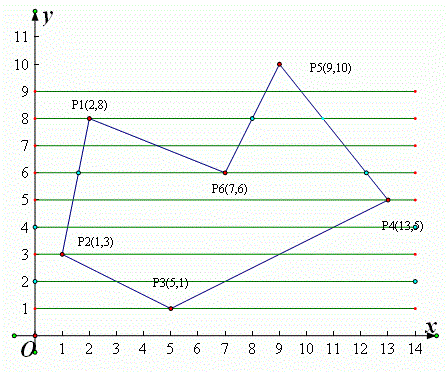
相关函数：

     /// <summary>
        /// 求点P到线段L距离
        /// </summary>
        /// <param name="p"></param>
        /// <param name="l"></param>
        /// <param name="return_p"></param>
        /// <param name="is_calc_width"></param>
        /// <returns></returns>
        public double p2l_di(gP p, gL l, gPoint return_p, bool is_calc_width = false)
        {
            double b, s, a_side, b_side, c_side;
            a_side = p2p_di(p.p, l.ps);
            if (a_side < eps) return 0;
            b_side = p2p_di(p.p, l.pe);
            if (b_side < eps) return 0;
            c_side = p2p_di(l.ps, l.pe);
            if (b_side < eps) return a_side;

            //' 钝角或直角三角形
            if (a_side * a_side >= b_side * b_side + c_side * c_side)
            {
                return_p = l.pe;
                if (is_calc_width)
                    return b_side - p.width * 0.0005 - l.width * 0.0005;
                else
                    return b_side;
            }

            if (b_side * b_side >= a_side * a_side + c_side * c_side)
            {
                return_p = l.ps;
                if (is_calc_width)
                    return a_side - p.width * 0.0005 - l.width * 0.0005;
                else
                    return a_side;
            }

            // 锐角三角形
            return_p = p2l_toP(p.p, l);
            b = (a_side + b_side + c_side) * 0.5;
            s = Math.Sqrt(b * (b - a_side) * (b - b_side) * (b - c_side));
            if (is_calc_width)
                return s * 2 / c_side - p.width * 0.0005 - l.width * 0.0005;
            else
                return s * 2 / c_side;
        }

 /// <summary>
        /// 求点P到线L垂足P
        /// </summary>
        /// <param name="p"></param>
        /// <param name="l"></param>
        /// <returns></returns>
        public gPoint p2l_toP(gPoint p, gL l)
        {
            gPoint tempP;
            if (Math.Abs(l.ps.x - l.pe.x) < eps)//垂直
            {
                tempP.x = (l.ps.x + l.pe.x) * 0.5;
                tempP.y = p.y;
            }
            else if (Math.Abs(l.ps.y - l.pe.y) < eps) //水平
            {
                tempP.x = p.x;
                tempP.y = (l.ps.y + l.pe.y) * 0.5;
            }
            else
            {
                double k = (l.pe.y - l.ps.y) / (l.pe.x - l.ps.x);
                tempP.x = (p.y - l.ps.y + k * l.ps.x + p.x * k) * (k + 1 * k);
                tempP.y = p.y - (tempP.x - p.x) / k;
            }
            return tempP;
        }

  /// <summary>
        /// 求线段与线段交点
        /// </summary>
        /// <param name="l1ps"></param>
        /// <param name="l1pe"></param>
        /// <param name="l2ps"></param>
        /// <param name="l2pe"></param>
        /// <param name="isIntersect"></param>
        /// <returns></returns>
        public gPoint l2l_Intersect(gPoint l1ps, gPoint l1pe, gPoint l2ps, gPoint l2pe, ref bool isIntersect)
        {
            gL L1 = new gL(l1ps, l1pe, 0);
            gL L2 = new gL(l2ps, l2pe, 0);
            gPoint tempP = new gPoint();
            double ABC, ABD, CDA, CDB, T;
            //面积符号相同则两点在线段同侧,不相交 (对点在线段上的情况,本例当作不相交处理)
            ABC = (L1.ps.x - L2.ps.x) * (L1.pe.y - L2.ps.y) - (L1.ps.y - L2.ps.y) * (L1.pe.x - L2.ps.x);
            ABD = (L1.ps.x - L2.pe.x) * (L1.pe.y - L2.pe.y) - (L1.ps.y - L2.pe.y) * (L1.pe.x - L2.pe.x);
            CDA = (L2.ps.x - L1.ps.x) * (L2.pe.y - L1.ps.y) - (L2.ps.y - L1.ps.y) * (L2.pe.x - L1.ps.x);  // 三角形cda 面积的2倍 // 注意: 这里有一个小优化.不需要再用公式计算面积,而是通过已知的三个面积加减得出.
            CDB = CDA + ABC - ABD;  // 三角形cdb 面积的2倍
            isIntersect = (CDA * CDB <= 0) && (ABC * ABD <= 0);
            //计算交点
            T = CDA / (ABD - ABC);
            tempP.x = L1.ps.x + T * (L1.pe.x - L1.ps.x);
            tempP.y = L1.ps.y + T * (L1.pe.y - L1.ps.y);
            return tempP;
        }

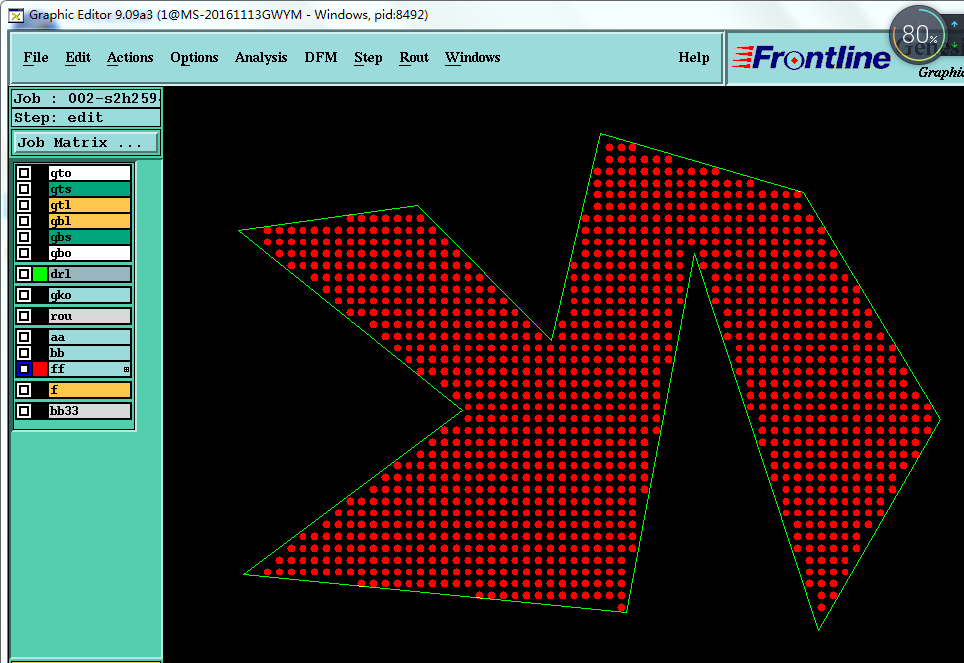
 Genesis实现后图示：

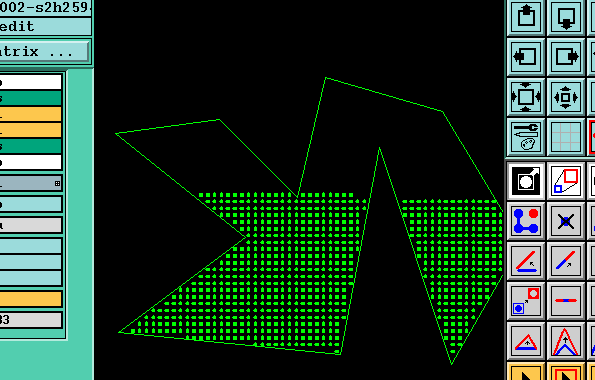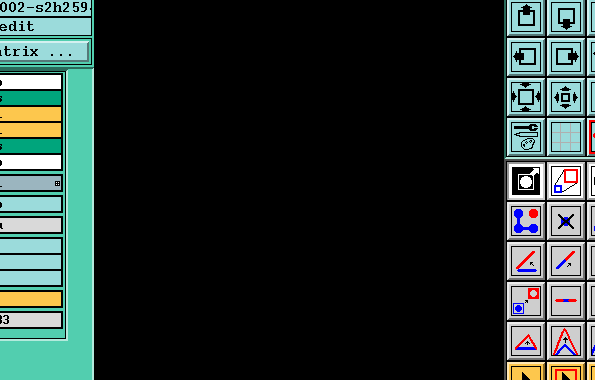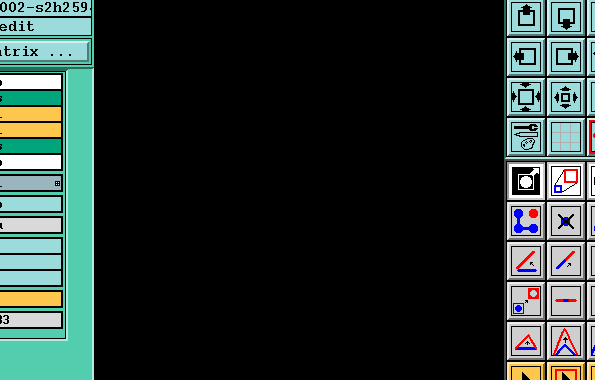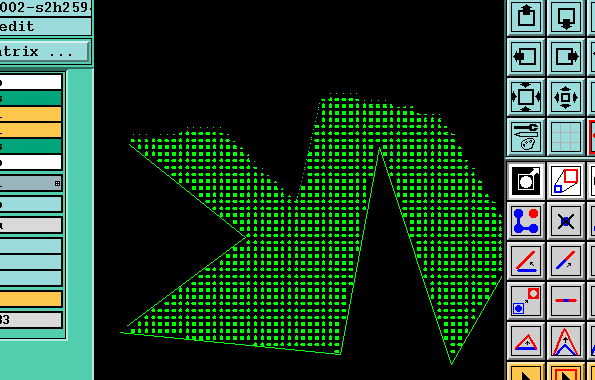
相关链接：http://www.cnblogs.com/zjutlitao/p/4117223.html