题目原意很简单,就是解一个三元一次方程组
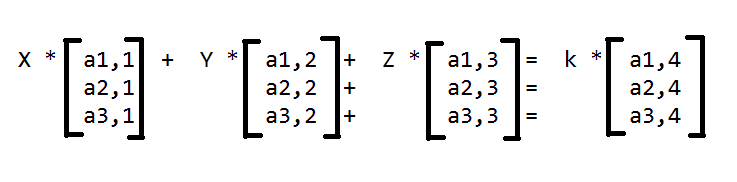
直接高斯消元解方程组,枚举最后一列的倍数(k)
注意double的精度,有很多细节需要处理

1 /* 2 PROB:ratios 3 LANG:C++ 4 */ 5 6 #include <stdio.h> 7 #include <math.h> 8 #include <algorithm> 9 #include <iostream> 10 using namespace std; 11 #define maxn 5 12 double A[5][5],a[5][5]; 13 14 typedef double Matrix[maxn][maxn]; 15 16 void solve(Matrix A,int n) 17 { 18 int i,j,k,r; 19 20 for (i=0;i<n;i++) 21 { 22 r=i; 23 for (j=i+1;j<n;j++) 24 if (fabs(A[j][i])>fabs(A[r][i])) 25 r=j; 26 if (r!=i) 27 for (j=0;j<=n;j++) 28 swap(A[r][j],A[i][j]); 29 30 for (k=i+1;k<n;k++) 31 { 32 double f=A[k][i]/A[i][i]; 33 for (j=i;j<=n;j++) 34 A[k][j]-=f*A[i][j]; 35 } 36 } 37 for (i=n-1;i>=0;i--) 38 { 39 for (j=i+1;j<n;j++) 40 A[i][n]-=A[j][n]*A[i][j]; 41 A[i][n]/=A[i][i]; 42 } 43 } 44 45 bool satisify(double x,double y,double z) 46 { 47 int t1=x+0.5,t2=y+0.5,t3=z+0.5; //+0.5四舍五入,处理精度问题 48 //比如原来是4.9999999,直接转成int就成了4,完蛋啦T^T 49 double xx=x-t1,yy=y-t2,zz=z-t3; 50 double comp=pow(10,-5); //double的比较法= =,差值小于10^-10就算相等了 51 if ((fabs(xx)<=comp)&&(fabs(yy)<=comp)&&(fabs(zz)<=comp)) 52 return true; 53 else 54 return false; 55 } 56 57 int main() 58 { 59 freopen("ratios.in","r",stdin); 60 freopen("ratios.out","w",stdout); 61 62 int x,y,z,t1,t2,t3; 63 double dx,dy,dz; 64 bool sol=false; 65 66 scanf("%d %d %d",&x,&y,&z); 67 //A[0][3]=x; A[1][3]=y; A[2][3]=z; 68 t1=x; t2=y; t3=z; 69 scanf("%d %d %d",&x,&y,&z); 70 A[0][0]=x; A[1][0]=y; A[2][0]=z; 71 scanf("%d %d %d",&x,&y,&z); 72 A[0][1]=x; A[1][1]=y; A[2][1]=z; 73 scanf("%d %d %d",&x,&y,&z); 74 A[0][2]=x; A[1][2]=y; A[2][2]=z; 75 /* 76 for (int i=0;i<=2;i++) 77 { 78 for (int j=0;j<=3;j++) 79 printf("%.8f ",A[i][j]); 80 printf(" "); 81 } 82 */ 83 for (int i=1;i<=100;i++) 84 { 85 for (int i=0;i<=2;i++) 86 for (int j=0;j<=3;j++) 87 a[i][j]=A[i][j]; 88 a[0][3]=t1*i; 89 a[1][3]=t2*i; 90 a[2][3]=t3*i; 91 //printf("%.8f %.8f %.8f ",a[0][3],a[1][3],a[2][3]); 92 solve(a,3); 93 dx=a[0][3]; dy=a[1][3]; dz=a[2][3]; 94 //printf("%.8f %.8f %.8f ",dx,dy,dz); 95 if (satisify(dx,dy,dz)) 96 { 97 sol=true; 98 int xx=dx,yy=dy,zz=dz; 99 //printf("%d %d %d ",xx,yy,zz); 100 if (xx<0||yy<0||zz<0) 101 printf("NONE "); 102 else 103 { 104 xx=dx+0.5; yy=dy+0.5; zz=dz+0.5; 105 printf("%d %d %d %d ",xx,yy,zz,i); 106 } 107 break; 108 } 109 //printf("%.8f %.8f %.8f ",a[0][3],a[1][3],a[2][3]); 110 } 111 if (!sol) printf("NONE "); 112 113 } 114 115 /* 116 117 118 int main() //垃圾代码,一开始YY的错了 119 { 120 freopen("ratios.in","r",stdin); 121 freopen("ratios.out","w",stdout); 122 123 double a1,a2,a3,a0,b1,b2,b3,b0,c1,c2,c3,c0,A0,A1,A2,A3,B0,B1,B2,B3,C0,C1,C2,C3; 124 int xx,yy,zz; 125 bool sol=false; 126 cin>>A0>>B0>>C0; 127 cin>>A1>>B1>>C1; //line1 128 cin>>A2>>B2>>C2; //line2 129 cin>>A3>>B3>>C3; //line3 130 131 for (int i=1;i<=100;i++) 132 { 133 a0=A0*i; a1=A1; a2=A2; a3=A3; 134 b0=B0*i; b1=B1; b2=B2; b3=B3; 135 c0=C0*i; c1=C1; c2=C2; c3=C3; 136 137 double t0=b1*c1,t1=c1*a1,t2=a1*b1; 138 a1=a1*t0; a2=a2*t0; a3=a3*t0; a0=a0*t0; 139 b1=b1*t1; b2=b2*t1; b3=b3*t1; b0=b0*t1; 140 c1=c1*t2; c2=c2*t2; c3=c3*t2; c0=c0*t2; 141 c1=c1-a1; c2=c2-a2; c3=c3-a3; c0=c0-a0; 142 b1=b1-a1; b2=b2-a2; b3=b3-a3; b0=b0-a0; 143 t0=c2; t1=b2; 144 b1=b1*t0; b2=b2*t0; b3=b3*t0; b0=b0*t0; 145 c1=c1*t1; c2=c2*t1; c3=c3*t1; c0=c0*t1; 146 c1=c1-b1; c2=c2-b2; c3=c3-b3; c0=c0-b0; 147 double z=c0/c3; 148 double y=(b0-b3*z)/b2; 149 double x=(a0-a3*z-a2*y)/a1; 150 printf("%%f %f %f ",x,y,z); 151 if (satisify(x,y,z)) 152 { 153 sol=true; 154 xx=x,yy=y,zz=z; 155 if (xx<0||yy<0||zz<0) 156 printf("NONE "); 157 else 158 printf("%d %d %d %d ",xx,yy,zz,i); 159 break; 160 } 161 } 162 if (!sol) printf("NONE "); 163 return 0; 164 } 165 */
扩展:POJ 1222
一个很著名的问题...
需要用高斯消元解带mod的方程组.....真心没看懂
http://mathworld.wolfram.com/LightsOutPuzzle.html
http://www.cnblogs.com/devtang/archive/2012/07/24/2606728.html
