hdu 6058 Kanade's sum

题目链接：【http://acm.hdu.edu.cn/showproblem.php?pid=6058】

题意：给出一个1-n的排列，然后让你求函数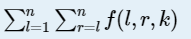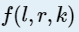，表示区间[l,r]的第k大的数。

题解：

这题能做？首先我们要知道第k大什么意思，注意不要理解成了第k小。我们维护每个数的贡献，其中【1，N-k+1】这些数是有贡献的，大于这些数是没有贡献的，然后我们选择从小到大维护一个东西，即从1开始，在左边找到k个比他大的数，在右边找到K个比他大的数，答案就可以维护了，然后把维护完的数删除，这个东西用双向链表维护。不知道怎么维护答案的可以看代码。

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int maxn = 5e5 + 15;
int a[maxn], pos[maxn];
int pre[maxn], nxt[maxn];
int L[maxn], R[maxn], l, r;
int T, N, M;
LL ans = 0;
void Erase(int k)
{
    int p = pre[k];
    int n = nxt[k];
    if(p) nxt[ p ] = n;
    if(n <= N) pre[n] = p;
    pre[k] = nxt[k] = 0 ;
}
int main ()
{
    scanf("%d", &T);
    while(T--)
    {
        scanf("%d %d", &N, &M);
        for(int i = 1; i <= N; i++)
        {
            scanf("%d", &a[i]);
            pos[a[i]] = i;
            pre[i] = i - 1;
            nxt[i] = i + 1;
        }
        ans  = 0;
        for(int k = 1; k <= N - M + 1 ; k++)
        {
            int p = pos[k];
            l = r = 0;
            for(int i = p; i && l <= M + 1; i = pre[i]) L[++l] = i;
            for(int i = p; i <= N && r <= M + 1; i = nxt[i]) R[++r] = i;
            L[++l] = 0;
            R[++r] = N + 1;
            for(int i = 1; i <= l - 1 && i <= M; i++)
            {
                if(M - i + 1 <= r - 1)
                {
                    LL lsum = (LL)(L[i] - L[i + 1]);
                    LL rsum = (LL)(R[M - i + 2] - R[M - i + 1]);
                    LL num =  (LL)k;
                    ans += lsum * rsum * num;
                }
            }
            Erase(p);
            //printf("%lld
", ans);
        }
        printf("%lld
", ans);
    }
    return 0;
}