迭代和递归

递归

递归就是一个问题可以不断分解成类似的子问题，对应就是一个函数不断调用自身，通过求解更小的子问题来实现原问题的求解。

递归的两个必备要素是：① 在函数里面调用自身 ② 有递归出口，不能无限制的调用自身，最终可以转化为非递归的情况。也就是函数中有初始值（Base case），之后会结合代码实例具体讲解。

下面是一个斐波那契数列的递归实现：（python）

# recursion
def Fibnacii_rec(n):
    if 0<=n<=1: # base case
        return n
    elif n>1:
        return Fibnacii_rec(n-1)+Fibnacii_rec(n-2)
    else:
        print("error")

迭代

迭代就是利用变量的原值计算出新的值。

下面是一个斐波那契数列的迭代实现：

# iteration
def Fibnacii_ite(n):
    if 0<=n<=1:
        return n
    n0=0
    n1=1
    its=n-1
    n_next=0
    while its>0: # n_next is updated iteratively
        its-=1
        n_next=n0+n1
        n0=n1
        n1=n_next
    return n_next

调用两函数，比较计算时间

def call_fib(function,n):
    time_s = time.time()
    print(function(n))
    time_e = time.time()
    print(str(function).split(' ')[1]+":", time_e - time_s)
call_fib(Fibnacii_rec,30)
call_fib(Fibnacii_ite,30)

运行结果如下：

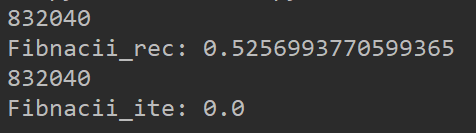
我们可以看到当n=30时，递归已经需要0.5s，而迭代还是0，当n越大差异越明显。

总结，递归效率比较低，尤其在输入较大的时候，并且递归太深有堆栈溢出的问题。

ref:

https://blog.csdn.net/swliao/article/details/5337896

https://blog.csdn.net/qq_40817827/article/details/89950325?depth_1-utm_source=distribute.pc_relevant.none-task&utm_source=distribute.pc_relevant.none-task