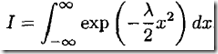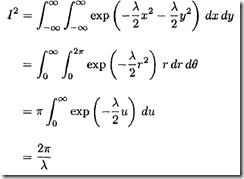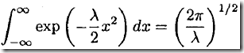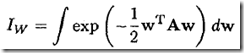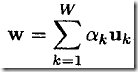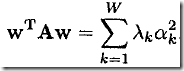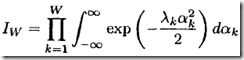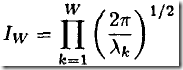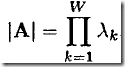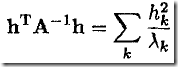1.单变量
单变量积分：
要完成上面积分，可通过考虑积分的平方，并转换到极坐标系（
，
）来巧妙实现
得 
（1）
2.多变量积分
W维的高斯积分，A是W*W维的实对称阵，w是W维的向量：
（2）
直接对上式积分是非常困难的，因为它涉及到对整个权重空间（有可能维数很高）进行积分。这时，就像我们解决负责问题时总是将其分解为小的易解决的小问题一样，利用Appdendix A 中矩阵分解的思想（注意，这里被劫函数其实是一个二次型）来做，具体步骤如下：
1）基于A的特征式
，将W分解为A的特征向量的线性组合
2）利用
的正交性，有
3）将上面两式带入式（1），从而将对
积分转换为对
的积分
注意这个转换可不简单，它同时实现了解偶，即将多重积分转换为多个单积分的乘积。这样每个单积分非常好算，而乘法就更简单了。Great Ideas！
同时要注意，这里之所以能获得最终的转换，即依赖于A为正定对称阵，从而实现分解；也依赖于此处是高斯积分，指数函数可以将乘法转换为指数系数的加法。
4）从而有
，因
，最终可得
（3）
3.加入线性项
考虑更一般的高斯积分，增加线性项
它的积分处理思路与上面一样
1）对
做变换，得它在特征向量上的映射
，得到如下分解
2）由于
，同时变化积分变量为
，从而得
3）由于
，上式变化为
（4）
