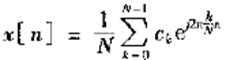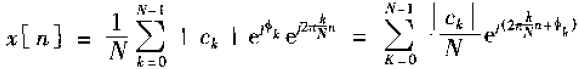数字信号处理 － chap5 数字信号频谱

5.1 频谱的意义

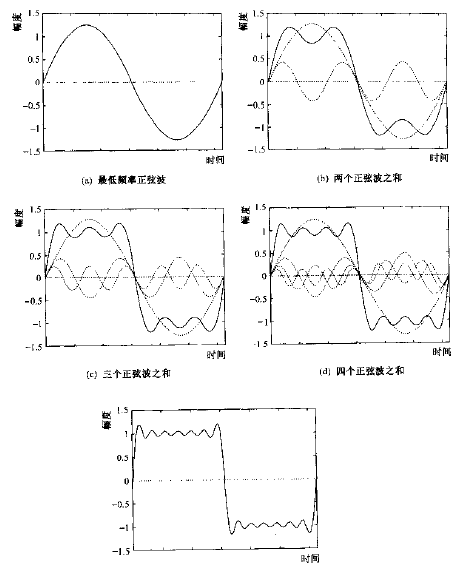
信号的频谱(spectrum)描述了信号包含的频率分量。信号的平稳变化源于它的低频分量，急剧变化源于它的高频分量。对方波来说，它即包括产生平稳变化的低频分量，也包括形成陡峭边缘的高频分量。

5.2 非周期数字信号

非周期信号的DTFT（离散傅里叶变换）给出了它的频谱:

1）计算需要信号的所有采样值

2）当信号有无限多个递减的采样值时，可在其降到某个阈值之和，截断信号，从而计算出近似的DTFT

 

频谱可表示为复数形式

1）幅度频谱： 对 的曲线

2）相位谱： 对 的曲线

5.3 周期数字信号

由于周期信号是同一段序列在时域不断重复，因此导致DTFT结果为无限，所以DTFT不适合计算它的频谱。用来计算周期信号频谱的工具为离散傅里叶级数（discrete Fourier series， DFS）。

周期为N的傅里叶级数为                           （1）

1）傅里叶系数为 。由于x[n]的周期为N，所以求系数 只需任意N个相继采样值，且它也仅有N个主值，并不断重复

2）1/N乘子是保证从傅里叶展开恢复x[n]的比例因子

 

系数为复数，它的极坐标形式为 ，带入式（1）有傅里叶级数的另一种形式

                     （2）

对比数字正弦的一般形式 ，可知

1） 含有幅度信息

2） 含有相位信息

3）k与频率成正比   即

                                                     （3）

4）式（3）显示了傅里叶级数所有分量的频率。k＝0是直流分量；k＝1是一次谐波（基频），它的倒数是信号完成一个完整循环的时间，这个时间等于NTs。

5）离散傅里叶级数包含了0到 的频率，因此N个傅里叶级数的系数位于0到接近采样频率的频率上。

 

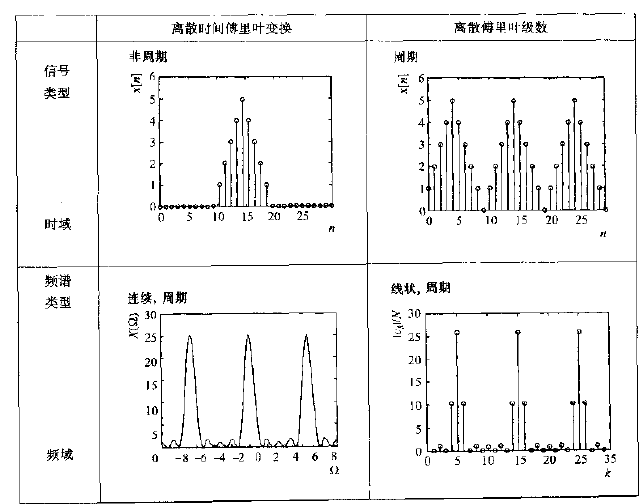
5.4 DTFT和DFS的关系

DTFT产生连续频谱（在所有频率处都有值），因而非周期信号的频谱是连续曲线。

DFS产生不连续频谱（仅在N点上有值），因而周期信号的频谱是等间隔的竖线。