原文链接:http://www.one2know.cn/keras6/
- LSTM 是 long-short term memory 的简称, 中文叫做 长短期记忆. 是当下最流行的 RNN 形式之一
- RNN 的弊端
RNN没有长久的记忆,比如一个句子太长时开头部分可能会忘记,从而给出错误的答案。
时间远的记忆要进过长途跋涉才能抵达最后一个时间点. 然后我们得到误差, 而且在 反向传递 得到的误差的时候, 他在每一步都会 乘以一个自己的参数 W. 如果这个 W 是一个小于1 的数, 比如0.9. 这个0.9 不断乘以误差, 误差传到初始时间点也会是一个接近于零的数, 所以对于初始时刻, 误差相当于就消失了. 我们把这个问题叫做梯度消失或者梯度弥散 Gradient vanishing. 反之如果 W 是一个大于1 的数, 比如1.1 不断累乘, 则到最后变成了无穷大的数, RNN被这无穷大的数撑死了, 这种情况我们叫做梯度爆炸, Gradient exploding. 这就是普通 RNN 没有办法回忆起久远记忆的原因。 - LSTM网络

在上图中,每一行携带一个完整的向量,从一个节点的输出到另一个节点的输入。粉红的圆圈代表逐点操作,如矢量加法,而黄色的方框是学习神经网络层。行合并表示连接,而行分叉表示复制的内容以及复制到不同位置的内容。 - 核心理念
LSTM的关键是单元状态,即贯穿图顶部的水平线。单元状态有点像传送带。它沿着整个链条直行,只有一些微小的线性相互作用。信息很容易保持不变地沿着它流动。
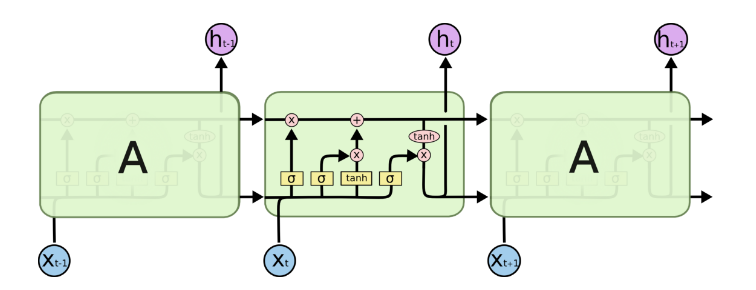
LSTM可以去除或增加单元状态的信息,并被称为门(gates)的结构仔细调控,它们由一个sigmoid神经网络层和一个逐点乘法运算组成。sigmoid输出层的输出介于0和1之间的数字,描述每个组件应该通过多少,0表示不让任何东西通过,1表示可以通过。 - 遗忘门
遗忘门(forget gate)顾名思义,是控制是否遗忘的,在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态。遗忘门子结构如下图:
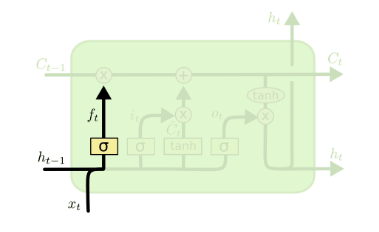
图中输入的有上一序列的隐藏状态h(t−1)和本序列数据x(t),通过一个激活函数,一般是sigmoid,得到遗忘门的输出f(t)。由于sigmoid的输出f(t)在[0,1]之间,因此这里的输出f^{(t)}代表了遗忘上一层隐藏细胞状态的概率。用数学表达式即为:
f(t)=σ(Wfh(t−1)+Ufx(t)+bf)f(t)=σ(Wfh(t−1)+Ufx(t)+bf)
其中Wf,Uf,bfWf,Uf,bf为线性关系的系数和偏倚,和RNN中的类似,σ为sigmoid激活函数。 - 输入门
输入门(input gate)负责处理当前序列位置的输入,它的子结构如下图:

从图中可以看到输入门由两部分组成,第一部分使用了sigmoid激活函数,输出为i(t),第二部分使用了tanh激活函数,输出为a(t), 两者的结果后面会相乘再去更新细胞状态。用数学表达式即为:
i(t)=σ(Wih(t−1)+Uix(t)+bi)i(t)=σ(Wih(t−1)+Uix(t)+bi)
a(t)=tanh(Wah(t−1)+Uax(t)+ba)a(t)=tanh(Wah(t−1)+Uax(t)+ba)
其中Wi,Ui,bi,Wa,Ua,ba,Wi,Ui,bi,Wa,Ua,ba,为线性关系的系数和偏倚,和RNN中的类似,σσ为sigmoid激活函数。 - 细胞状态更新
在研究LSTM输出门之前,我们要先看看LSTM之细胞状态。前面的遗忘门和输入门的结果都会作用于细胞状态C(t)。我们来看看从细胞状态C(t−1)如何得到C(t)。如下图所示:

细胞状态C(t)由两部分组成,第一部分是C(t−1)和遗忘门输出f(t)f(t)的乘积,第二部分是输入门的i(t)和a(t)的乘积,即:
C(t)=C(t−1)⊙f(t)+i(t)⊙a(t)C(t)=C(t−1)⊙f(t)+i(t)⊙a(t)
其中,⊙为Hadamard积(对应位置相乘),在DNN中也用到过。 - 输出门
有了新的隐藏细胞状态C(t),我们就可以来看输出门了,子结构如下:

从图中可以看出,隐藏状态h(t)的更新由两部分组成,第一部分是o(t), 它由上一序列的隐藏状态h(t−1)和本序列数据x(t),以及激活函数sigmoid得到,第二部分由隐藏状态C(t)和tanh激活函数组成, 即:
o(t)=σ(Woh(t−1)+Uox(t)+bo)o(t)=σ(Woh(t−1)+Uox(t)+bo)
h(t)=o(t)⊙tanh(C(t))h(t)=o(t)⊙tanh(C(t))
通过本节的剖析,相信大家对于LSTM的模型结构已经有了解了。当然,有些LSTM的结构和上面的LSTM图稍有不同,但是原理是完全一样的。 - LSTM前向传播算法
LSTM模型有两个隐藏状态h(t),C(t),模型参数几乎是RNN的4倍,因为现在多了Wf,Uf,bf,Wa,Ua,ba,Wi,Ui,bi,Wo,Uo,boWf,Uf,bf,Wa,Ua,ba,Wi,Ui,bi,Wo,Uo,bo这些参数。
前向传播过程在每个序列索引位置的过程为:
1)更新遗忘门输出:
f(t)=σ(Wfh(t−1)+Ufx(t)+bf)f(t)=σ(Wfh(t−1)+Ufx(t)+bf)
2)更新输入门两部分输出:
i(t)=σ(Wih(t−1)+Uix(t)+bi)i(t)=σ(Wih(t−1)+Uix(t)+bi)
a(t)=tanh(Wah(t−1)+Uax(t)+ba)a(t)=tanh(Wah(t−1)+Uax(t)+ba)
3)更新细胞状态:
C(t)=C(t−1)⊙f(t)+i(t)⊙a(t)C(t)=C(t−1)⊙f(t)+i(t)⊙a(t)
4)更新输出门输出:
o(t)=σ(Woh(t−1)+Uox(t)+bo)o(t)=σ(Woh(t−1)+Uox(t)+bo)
h(t)=o(t)⊙tanh(C(t))h(t)=o(t)⊙tanh(C(t))
5)更新当前序列索引预测输出:
ŷ (t)=σ(Vh(t)+c)y^(t)=σ(Vh(t)+c) - LSTM反向传播算法
有了LSTM前向传播算法,推导反向传播算法就很容易了, 思路和RNN的反向传播算法思路一致,也是通过梯度下降法迭代更新我们所有的参数,关键点在于计算所有参数基于损失函数的偏导数。
在RNN中,为了反向传播误差,我们通过隐藏状态h(t)的梯度δ(t)一步步向前传播。在LSTM这里也类似,只不过我们这里有两个隐藏状态h(t)和C(t),这里我们定义两个δ,即:
δ(t)h=∂L∂h(t)δh(t)=∂L∂h(t)
δ(t)C=∂L∂C(t)δC(t)=∂L∂C(t)
反向传播时只使用了δ(t)CδC(t),变量δ(t)hδh(t)仅为帮助我们在某一层计算用,并没有参与反向传播,这里要注意。如下图所示:

而在最后的序列索引位置ττ的δ(τ)hδh(τ)和 δ(τ)CδC(τ)为:
δ(τ)h=∂L∂O(τ)∂O(τ)∂h(τ)=VT(ŷ (τ)−y(τ))δh(τ)=∂L∂O(τ)∂O(τ)∂h(τ)=VT(y^(τ)−y(τ))
δ(τ)C=∂L∂h(τ)∂h(τ)∂C(τ)=δ(τ)h⊙o(τ)⊙(1−tanh2(C(τ)))δC(τ)=∂L∂h(τ)∂h(τ)∂C(τ)=δh(τ)⊙o(τ)⊙(1−tanh2(C(τ)))
接着我们由δ(t+1)CδC(t+1)反向推导δ(t)CδC(t)。
δ(t)hδh(t)的梯度由本层的输出梯度误差决定,即:
δ(t)h=∂L∂h(t)=VT(ŷ (t)−y(t))δh(t)=∂L∂h(t)=VT(y^(t)−y(t))
而δ(t)CδC(t)的反向梯度误差由前一层δ(t+1)CδC(t+1)的梯度误差和本层的从h(t)h(t)传回来的梯度误差两部分组成,即:
δ(t)C=∂L∂C(t+1)∂C(t+1)∂C(t)+∂L∂h(t)∂h(t)∂C(t)=δ(t+1)C⊙f(t+1)+δ(t)h⊙o(t)⊙(1−tanh2(C(t)))
δC(t)=∂L∂C(t+1)∂C(t+1)∂C(t)+∂L∂h(t)∂h(t)∂C(t)=δC(t+1)⊙f(t+1)+δh(t)⊙o(t)⊙(1−tanh2(C(t)))
有了δ(t)hδh(t)和δ(t)CδC(t), 计算这一大堆参数的梯度就很容易了,这里只给出WfWf的梯度计算过程,其他的Uf,bf,Wa,Ua,ba,Wi,Ui,bi,Wo,Uo,bo,V,cUf,bf,Wa,Ua,ba,Wi,Ui,bi,Wo,Uo,bo,V,c的梯度大家只要照搬就可以了。
∂L∂Wf=∑t=1τ∂L∂C(t)∂C(t)∂f(t)∂f(t)∂Wf=∑t=1τδ(t)C⊙C(t−1)⊙f(t)⊙(1−f(t))(h(t−1))
T∂L∂Wf=∑t=1τ∂L∂C(t)∂C(t)∂f(t)∂f(t)∂Wf=∑t=1τδC(t)⊙C(t−1)⊙f(t)⊙(1−f(t))(h(t−1))T
LSTM 实例
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# 加载数据集
dataset_train = pd.read_csv('平安银行.csv',encoding='gb18030')
training_set = dataset_train.iloc[:,1:2].values
print(dataset_train.head()) # 查看一下数据的格式
# 特征缩放
from sklearn.preprocessing import MinMaxScaler
sc = MinMaxScaler(feature_range=(0,1))
training_set_scaled = sc.fit_transform(training_set)
# 使用Timesteps创建数据
X_train = []
y_train = []
for i in range(60, 2035):
X_train.append(training_set_scaled[i-60:i, 0]) # 训练集为早60个的数据
y_train.append(training_set_scaled[i, 0])
X_train, y_train = np.array(X_train), np.array(y_train)
X_train = np.reshape(X_train, (X_train.shape[0], X_train.shape[1], 1))
# 构建LSTM
from keras.models import Sequential
from keras.layers import Dense
from keras.layers import LSTM
from keras.layers import Dropout
regressor = Sequential()
regressor.add(LSTM(units = 50, return_sequences = True, input_shape = (X_train.shape[1], 1)))
regressor.add(Dropout(0.2))
regressor.add(LSTM(units = 50, return_sequences = True))
regressor.add(Dropout(0.2))
regressor.add(LSTM(units = 50, return_sequences = True))
regressor.add(Dropout(0.2))
regressor.add(LSTM(units = 50))
regressor.add(Dropout(0.2))
regressor.add(Dense(units = 1))
regressor.compile(optimizer = 'adam', loss = 'mean_squared_error')
regressor.fit(X_train, y_train, epochs = 20, batch_size = 32)
# 预测未来的股票
dataset_test = pd.read_csv('平安银行.csv',encoding='gb18030')
y_test = dataset_test.iloc[:, 1:2].values
dataset_total = pd.concat((dataset_train['开盘价(元)'], dataset_test['开盘价(元)']), axis = 0)
inputs = dataset_total[len(dataset_total) - len(dataset_test) - 60:].values
inputs = inputs.reshape(-1,1)
inputs = sc.transform(inputs)
X_test = []
for i in range(60, 76):
X_test.append(inputs[i-60:i, 0])
X_test = np.array(X_test)
X_test = np.reshape(X_test, (X_test.shape[0], X_test.shape[1], 1))
y_pred = regressor.predict(X_test)
predicted_stock_price = sc.inverse_transform(y_pred)
# 可视化
plt.plot(y_test, color = 'black', label = 'SZ000001 Price')
plt.plot(y_pred, color = 'green', label = 'Predicted SZ000001 Price')
plt.title('SZ000001 Price Prediction')
plt.xlabel('Time')
plt.ylabel('SZ000001 Price')
plt.legend()
plt.show()
输出:
