数据结构和算法
1.1 初识算法
- 算法就是用于解决特定问题的一系列的执行步骤
- 使用不同算法,解决同一个问题,效率却可能相差非常大
1.2 斐波那契算法
- 斐波那契数的形式:0、1、1、2、3、5、8
- n项 + (n+1)项 = n+2项 这种数列叫做斐波那契数
- 假定我们此时有方法 getFibonacci();
- 我们希望通过这个方法求第N项的斐波那契数是多少 如:getFibonacci(7) = 13
1.2.1 递归法
代码展示:
package com.jiang;
public class Code01_Fibonacci {
public static int getFibonacci(int n) {
//如果n<=1 其实都是返回的本身的值
if(n <= 1) {
return n;
}
//例如 传入n=3 求第1+第二位的值
return getFibonacci(n - 1) + getFibonacci(n - 2);
}
public static void main(String[] args) {
System.out.println(getFibonacci(7));
}
}
// getFibonacci(7) = 13
分析问题:
如果getFibonacci()参数传入的是177,那么你会发现他会进入很漫长的计算时间,迟迟得不到结果。
当然,最终问题是因为递归导致栈空间不够用,从而栈溢出,这将在后面详细讲解,目前有一定概念即可。
1.2.2 for循环版
代码展示:
public static int getFibonacci2(int n) {
//如果n<=1 其实都是返回的本身的值
if(n <= 1) {
return n;
}
//定义第一个和第二个的值
int first = 0;
int second = 1;
//以 get(3)为例
//i需要循环3-1 = 2次
for(int i = 0; i<n-1;i++) {
//第一次循环 sum初始是1
//第二次循环 sum = 1+1 = 2
int sum = first + second;
//第一次循环 first = 1;
//第二次循环 first = 1;
first = second;
//第一次循环 second = 1;
//第二次循环 second = 2;
second = sum;
}
return second;
}
此时我们输入177也可以快速的进行反应,这就有一个新的概念,复杂度
1.2.3 线性代数-特征方程
public static int getFibonacciByTezheng(int n) {
double c = Math.sqrt(5);
return (int)((Math.pow((1+c)/2, n) - Math.pow((1 - c) / 2, n)) /c);
}
时间复杂度:视为 O(1),不进行过多赘述,涉及到线性代数特征方程的知识点
1.3 如何评价算法的好坏
- 提出一个问题:对于斐波那契这个算法递归法和循环法那个代码看起来更好呢?
- 很明显,递归法看起来更好一点,当然只是指代码形式上的好,因为他的代码更少,更简洁。但是实际上性能来说循环方法要远远优于递归法
- 如果单从执行效率上进行评估,可能会想到这么一种方案
- 比较不同算法对同一组输入的执行处理时间
- 这种方案也叫做:事后统计法
- 上述方案有比较明显的缺点
- 执行时间严重依赖硬件以及运行时各种不确定的环境因素
- 必须编写相应的测算代码
- 测试数据的选择比较难保证公正性
- 一般从以下维度来评估算法的优劣
- 正确性、可读性、健壮性(对不合理输入的反应能力和处理能力)
- 时间复杂度(time complexity):估算程序指令的执行次数(执行时间)
- 空间复杂度(space complexity):估算所需占用的存储空间
1.4 大O表示法(Big O)
- 一般用大O表示法来描述复杂度,它表示的是数据规模 n 对应的复杂度
- 忽略常数、系数、低阶
- 9 >> O(1)
- 2n + 3 >> O(n)
- n^2 + 2n + 6 >> O(n^2)
- 4n^3 + 3n^2 + 22n + 100 >> O(n^3)
- 写法上,n^3 等价于 n的三次方
- 注意:大O表示法仅仅是一种粗略的分析模型,是一种估算,能帮助我们短时间内了解一个算法的执行效率
- 对数阶一般省略底数
- log2n = log2^9 ∗ log9n
- 所以 log2n 、log9n 统称为 logn
1.5 常见的复杂度
| 执行次数 | 复杂度 | 非正式术语 |
|---|---|---|
| 12 | O(1) | 常数阶 |
| 2n + 3 | O(n) | 线性阶 |
| 4n^2 + 2n + 6 | O(n^2) | 平方阶 |
| 4log2n + 25 | O(logn) | 对数阶 |
| 3n + 2nlog3n + 15 | O(nlogn) | nlogn阶 |
| 4n^3 + 3n^2 + 22n + 100 | O(n^3) | 立方阶 |
| 2^n | O(2^n) | 指数阶 |
- O(1) < O(logn) < O(n) < O(nlogn) < O(n^2 ) < O(n^3 ) < O(2^n ) < O(n!) < O(nn)
- 可以借助函数生成工具对比复杂度的大小
- https://zh.numberempire.com/graphingcalculator.php
1.6 不同数据下的复杂度
-
数据规模较小时
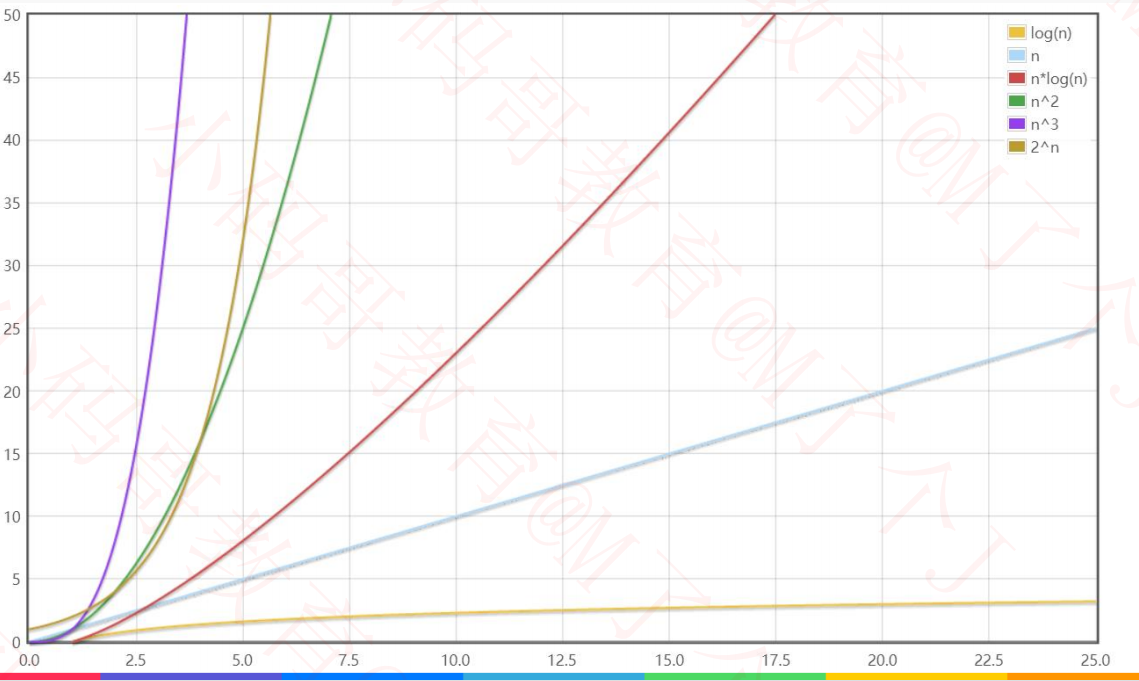
-
数据规模较大时
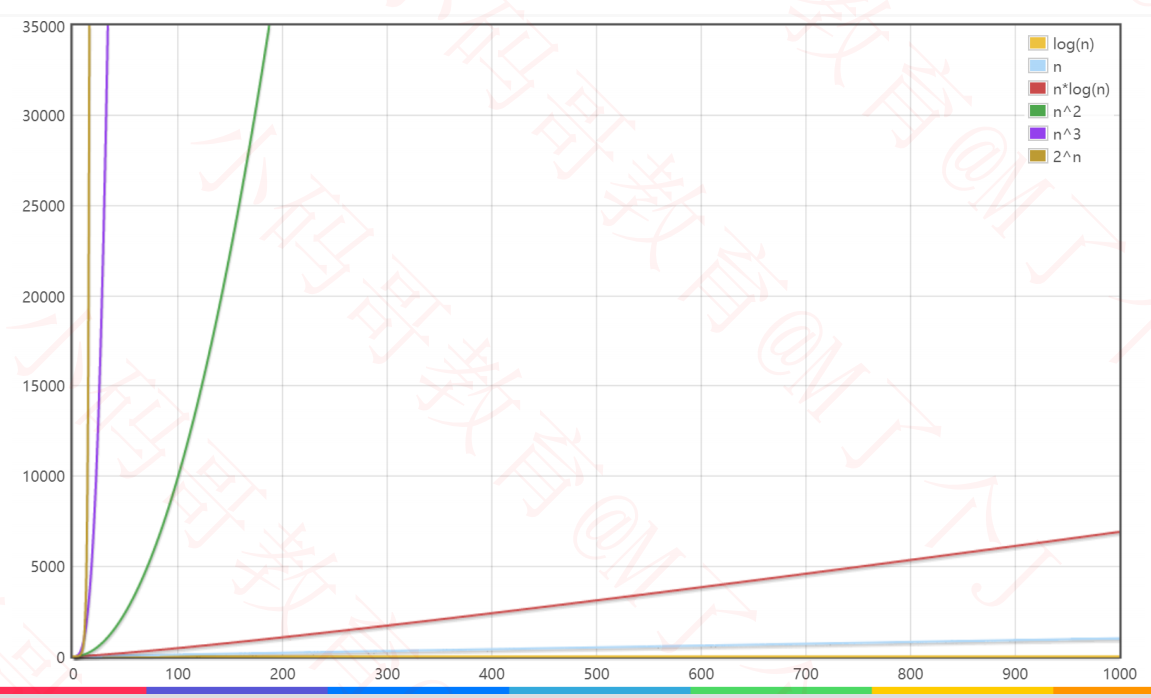
1.7 斐波那契数列复杂度
-
getFibonacciByFor循环
public static int getFibonacciByFor(int n) { if(n <= 1) { return n; } int first = 0; int second = 1; for(int i = 0; i<n-1;i++) { int sum = first + second; first = second; second = sum; } return second; }该复杂度可以分析出来 是由n控制的 是O(n)复杂度
-
getFibonacciBy递归
public static int getFibonacciByDigui(int n) { if(n <= 1) { return n; } return getFibonacci(n - 1) + getFibonacci(n - 2); }该方法中 最重要的是 最终return后的+的操作
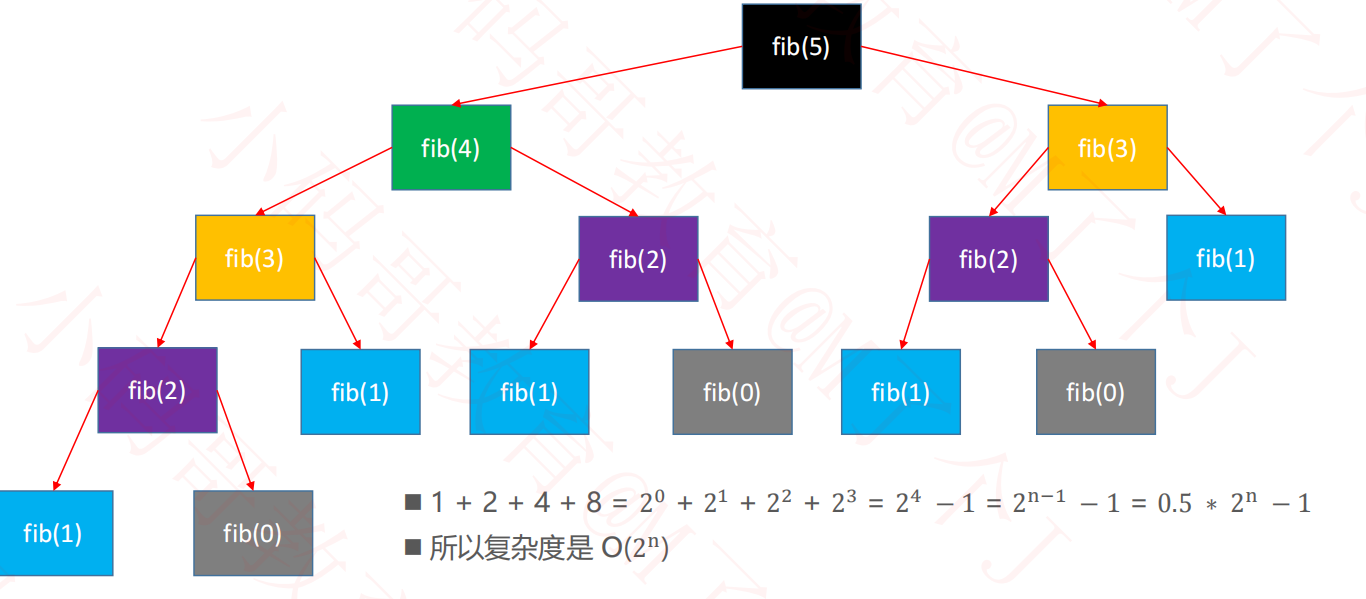
即复杂度是O(2^n),它的运行速度要大于O(n)
- 他们的差别有多大?
- 如果有一台1GHz的普通计算机,运算速度 109 次每秒( n 为 64 )
- O(n) 大约耗时 6.4 ∗ 10^(−8) 秒
- O(2n ) 大约耗时 584.94 年
- 有时候算法之间的差距,往往比硬件方面的差距还要大
1.8 算法的优化方向
- 用尽量少的存储空间
- 用尽量少的执行步骤(执行时间)
- 根据情况,可以
- 空间换时间
- 时间换空间