导数
[displaystyle frac{mathrm{d}(x)}{mathrm{d}x}=lim_{h o0}frac{f(x+h)-f(x)}{h}
]
h无限小,但是在python中不能设置得太小,否则会产生舍入误差。

np.float32最多到1e-45
由于h不可能无限接近0,(x + h)和x之间的斜率不能很好地近似x处的斜率,采用x+h和x-h来近似要更加精确。
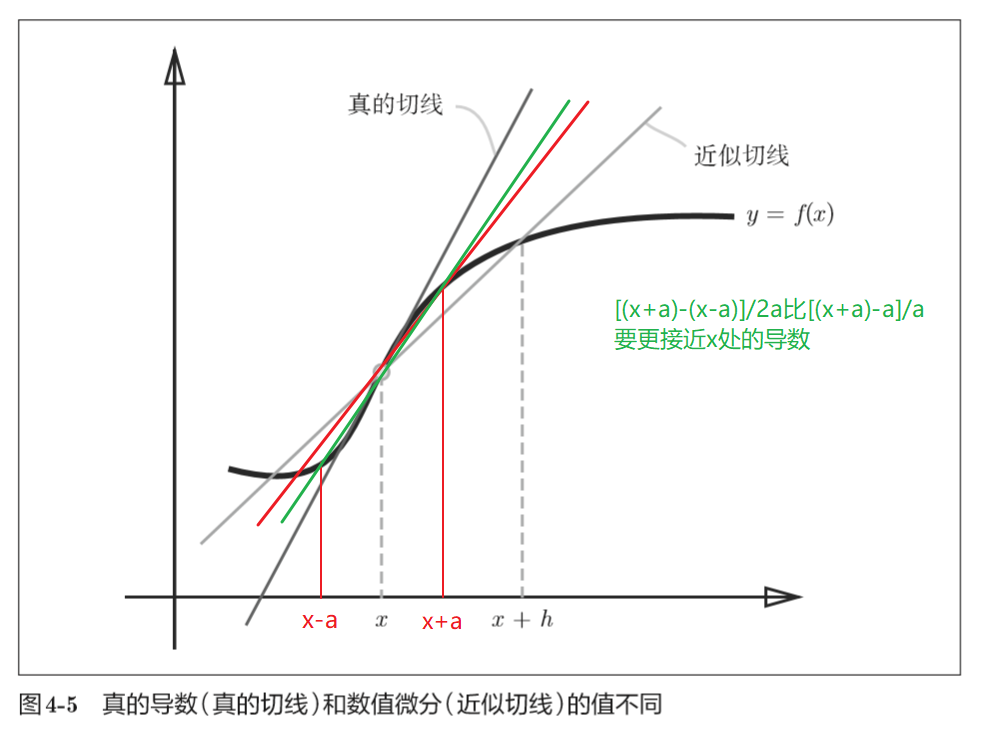
因此可以定义求导函数为
def numerical_diff(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)
利用微小的差分求导数的过程称为数值微分(numerical differentiation)。而基于数学式的推导求导数的过程,称为“解析性求解”或者“解析性求导”。比如,y = x^2的导数,可以通过解析性地求解出来。因此,当x = 2时, y的导数为4。解析性求导得到的导数是不含误差的“真的导数”。
梯度
像((dfrac{partial f}{partial x_0},dfrac{partial f}{partial x_1}))这样的由全部变量的偏导数汇总而成的向量称为梯度(gradient)。
梯度表示的是各点处的函数值减小最多的方向。
def numerical_gradient(f, x):
h = 1e-4 # 0.0001
grad = np.zeros_like(x)
for idx in range(x.size):
tmp_val = x[idx]
x[idx] = float(tmp_val) + h
fxh1 = f(x) # f(x+h)
x[idx] = tmp_val - h
fxh2 = f(x) # f(x-h)
grad[idx] = (fxh1 - fxh2) / (2*h)
x[idx] = tmp_val # 还原值
return grad
梯度下降法
函数的极小值、最小值以及鞍点(saddle point)处,梯度为0。
梯度法是要寻找梯度为0的地方,但是那个地 方不一定就是最小值(也有可能是极小值或者鞍点),只是沿着梯度的方向能够最大限度地减小函数的值。
[x_0=x_0-etadfrac{partial f}{partial x_0}\
x_1=x_1-etadfrac{partial f}{partial x_1}
]