Problem
题意概要:给定一个凸多边形坐标。点按顺时针编号 (1) 到 (n)。任意两点之间都有一条长度为欧氏距离的边相连。边相交处可以自由穿行。有 (m) 条边不能走,但是可以经过这条边与其他边的交点。问从点 (1) 到 (n) 的最短路(即给定完全图,删去(m)边,求最短路)
(nleq 10^5,mleq 10^6)
Solution
这个题还是挺巧妙的,只是画过图后就不难了
画两张图吧,就会发现只要贪心地往(n)号点走即可
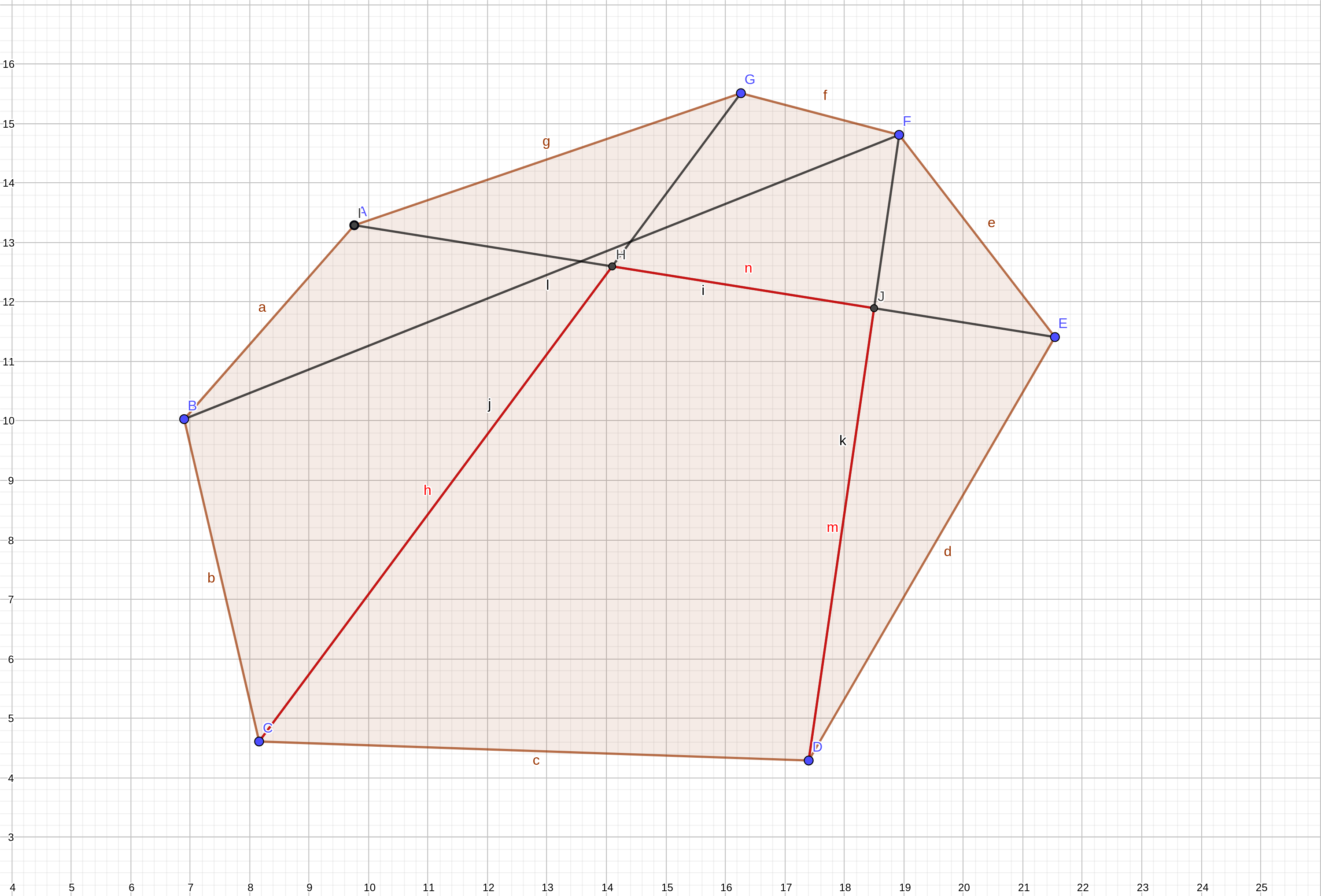
发现只要贴着里面走就行(走红色路线),进一步发现每个点连出去的的几条线只有最靠内的线有用
所以当前边数可以减少到(n)条,然后就……做半平面交((leftarrow)本题最巧妙的一点)
Code
#include <bits/stdc++.h>
using namespace std;
inline void read(int&x){
char c11=getchar(),ob=0;x=0;
while(c11^'-'&&!isdigit(c11))c11=getchar();if(c11=='-')ob=1,c11=getchar();
while(isdigit(c11))x=x*10+c11-'0',c11=getchar();if(ob)x=-x;
}
const int N=201009,M=2001003;
const double eps=1e-8;
int n,m;bool pass=false;
struct Paris{
int x,y;
friend inline bool operator < (const Paris&A,const Paris&B)
{return A.x!=B.x?A.x<B.x:A.y>B.y;}
}pr[M];
struct pnt{
double x,y;
inline pnt(){}
inline pnt(const double&X,const double&Y):x(X),y(Y){}
inline void in(){scanf("%lf%lf",&x,&y);}
friend inline pnt operator + (const pnt&A,const pnt&B) {return pnt(A.x+B.x,A.y+B.y);}
friend inline pnt operator - (const pnt&A,const pnt&B) {return pnt(A.x-B.x,A.y-B.y);}
friend inline double operator * (const pnt&A,const pnt&B) {return A.x*B.y-A.y*B.x;}
inline pnt operator * (const double&B) const {return pnt(x*B,y*B);}
}p[N],dot[N];
inline double dis(pnt A,pnt B){return sqrt((A.x-B.x)*(A.x-B.x)+(A.y-B.y)*(A.y-B.y));}
struct line{
pnt a,b;double slp;
inline void get_slp(){slp=atan2(b.y-a.y,b.x-a.x);}
friend inline bool operator < (const line&A,const line&B) {
if(fabs(A.slp-B.slp)>eps)
return A.slp<B.slp;
return (A.b-A.a)*(B.b-A.a)<0;
}
}l[N],q[N];
inline pnt crs(line A,line B){
double k1=(B.b-A.a)*(A.b-A.a);
double k2=(A.b-A.a)*(B.a-A.a);
return B.a+(B.b-B.a)*(k2/(k1+k2));
}
inline bool chk(line A,line B,line t){pnt p=crs(A,B);return (t.b-t.a)*(p-t.a)<0;}
void work(){
if(pass)return ;
for(int i=1;i<=n;++i)l[i].get_slp();
sort(l+1,l+n+1);
int tt=0;
for(int i=1;i<=n;++i)
if(fabs(l[i].slp-l[i-1].slp)>eps)
l[++tt]=l[i];
n=tt,tt=0;int L=1,R=0;
q[++R]=l[1],q[++R]=l[2];
for(int i=3;i<=n;++i){
while(L<R&&chk(q[R-1],q[R],l[i]))--R;
while(L<R&&chk(q[L],q[L+1],l[i]))++L;
q[++R]=l[i];
}
while(L<R&&chk(q[R-1],q[R],q[L]))--R;
while(L<R&&chk(q[L],q[L+1],q[R]))++L;
q[R+1]=q[L];
for(int i=L;i<=R;++i)
p[++tt]=crs(q[i],q[i+1]);
n=tt;
}
void input(){
read(n),read(m);
for(int i=1;i<=n;++i)dot[i].in();
for(int i=1;i<=m;++i)read(pr[i].x),read(pr[i].y);
for(int i=1;i<=n;++i)pr[++m].x=i,pr[m].y=i;
sort(pr+1,pr+m+1);
int tt;l[tt=1].a=dot[1],l[1].b=dot[n];
p[N-2].x=dot[1].x,p[N-2].y=dot[1].y;
p[N-1].x=dot[n].x,p[N-1].y=dot[n].y;
if(pr[1].x==1&&pr[1].y!=n){
printf("%.8lf
",dis(p[N-1],p[N-2]));
pass=true;return ;
}
for(int id=1,i=1,j;id<=n;++id){
while(i<=m&&pr[i].x<id)++i;j=n;
while(pr[i].x==id&&pr[i].y==j)++i,--j;
if(j>id)l[++tt].a=dot[j],l[tt].b=dot[id];
}n=tt;
}
void print(){
if(pass)return ;
p[n+1]=p[1];
double res=0.0;
for(int i=1;i<=n;++i)
res+=dis(p[i],p[i+1]);
res-=dis(p[N-1],p[N-2]);
printf("%.8lf
",res);
}
int main(){
input();
work();
print();
return 0;
}