先上一道题目:
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上x
-
求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3个整数,表示一个操作,具体如下:
操作1: 格式:1 x k 含义:将第x个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式:
输出包含若干行整数,即为所有操作2的结果。
输入输出样例
输入样例#1:
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
输出样例#1:
14
16
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=10000,M<=10000
对于100%的数据:N<=500000,M<=500000
想暴力过?不存在的(底层优化不敢说)。于是,我们需要一种数据结构来进行优化。
树状数组
其实,树状数组就是一个数组。
如果我们有一个数组(a),我们可以构造一个数组(C),使(C[i]=a[i-2^k+1]+cdots+a[i]),(k)为(i)在二进制下末尾(0)的个数。
这其实是一个绝妙的想法,因为(x)对应的(2^k)是十分好求的,我们称求(2^k)的函数为lowbit:
inline LL lowbit(LL x)
{
return x&(-x);
}
为什么呢?
首先,我们先来看看什么是补码:
一个数字的补码就是将该数字作比特反相运算(即反码),再将结果加1。在补码系统中,一个负数就是用其对应正数的补码来表示。
如:+8是00001000,而-8就是~8+1=11110111+1=11111000
如果(x)的二进制位末尾有(k)个(0),那么在取时,它们都会变成(1),加(1)之后,又都变成了(0)。又因为(x)的二进制位末尾只有(k)个(0),故第(k+1)位一定是(1),取反后变成(0),加(1)后,由于进位,又变成了(1),进位由此停止。与是,这两个数的二进制位上,除了第(k+1)位,其余应该都至少有一个是(0)((k)以前的为上补码一定是(0),可以后的位上有于取反,必定一位是(0),一位是(1))。由此可知,得到的答案是(2^k)。
其实,C数组就是一棵树状数组。
树状数组的结构如下图所示:
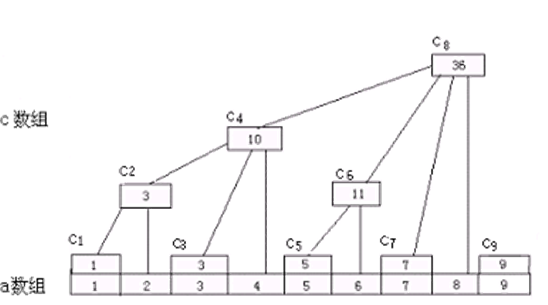
区间查询
个人感觉区间查询比单点修改,好理解。
首先,要查([l,r])的和,我们可以求出([1,l])的和,再减去([1,r))的和即可。于是问题就在于求出([1,ans])的和。
假设我们的树状数组为(a[l])(下文我们都这样假设,包括代码),我们首先查询(a[l]),得到的值是([l-2^{k_l}+1,l])的和。于是我们的问题就变成了求([1,i-2^{k_l},l])即([1,l-lowbit(l)])的和。我们发现这可以用递归实现。当然,一般我们都用循环实现(调用函数太慢),原理相同。
代码
inline LL sum(LL pla)
{
LL ans=0;
for(; pla; pla-=lowbit(pla))ans+=a[pla];
return ans;
}
单点修改
如果要在一个点加上一个数,由于我们需要在所有管得着该点的地方修改,于是我们必须知道:那些地方管得着。
让我们把那张图拿出来

看着图,我们就能发现:修改是查询的逆动作。管得着某点的地方就是从该点向上爬所经过的点。于是,我们只要模拟刚才查询的逆过程向上爬,即把pla-=lowbit(pla)改成pla+=lowbit(pla)即可。
代码
inline void add(LL pla,LL num)
{
for(; pla<=n; pla+=lowbit(pla))a[pla]+=num;
}
文章开头题目的代码
#include <cctype>
#include <cstdio>
typedef long long LL;
#define dd c=getchar()
template <class T>
inline void read(T &x)
{
x=0;char dd;bool f=false;
for(;!isdigit(c);dd)if(c=='-')f=true;
for(;isdigit(c);dd) x=(x<<1)+(x<<3)+(c^48);
if(f)x=-x;
return;
}
#undef dd
LL n;
LL a[500005];
inline LL lowbit(LL x)
{
return x&(-x);
}
inline void add(LL pla,LL num)
{
for(; pla<=n; pla+=lowbit(pla))a[pla]+=num;
}
inline LL sum(LL pla)
{
LL ans=0;
for(; pla; pla-=lowbit(pla))ans+=a[pla];
return ans;
}
int main()
{
LL m;
read(n);
read(m);
for(LL i=1; i<=n; ++i)
{
LL t;
read(t);
add(i,t);
}
while(m--)
{
LL a,b;
int t;
read(t);
read(a);
read(b);
if(t==1)add(a,b);
else printf("%lld
",sum(b)-sum(a-1));
}
return 0;
}