Link
https://jzoj.net/senior/#main/show/5257
Problem

Solution
5~90分
我们可以根据特殊性质搞
如果数据小,直接暴力在树上面模拟一次
如果满足性质1,就是第i条边连i和i+1地,那么就成了一条链,答案是可以按照数学方法计算出来的
如果满足性质2,就是A=C,那么就是A~B的长度,可以预处理快速求出来
这些分数,感谢出题人的馈赠
100分
其实我们可以画个图,粗略的画个图,看看答案是什么
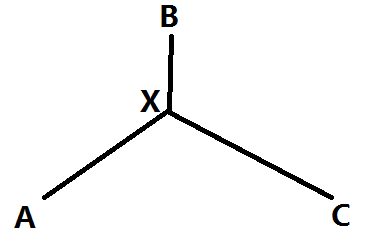
显然,根据这个图,我们就知道,答案其实就是BX这条线段的长度
怎么求?我们可以用最简单的容斥原理
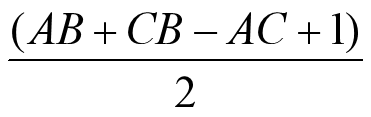
加一是因为X这个点之后要div2,所以应该得被计算2次
我们发现,求AB,CB,AC的方法,都是求他们到lca的长度
所以,我们可以用倍增,对他们做lca,并且记录路径长度
我们一次递归,预处理出,每个点的深度。
在递归中,顺便预处理f数组
其中f[i,j]表示第i个节点,在他上面第2j个节点是什么。
我们先把深度大的点,用倍增,弄成和另外一个节点一样的深度,这个和下面的方法类似
然后同时倍增。
其实就是找一个最大的j,满足f[a,j]不等于f[b,j],一直弄,最后就成了lca的两个儿子。
加法随便弄一下就行了。
其他两个求法类似,不在赘述了。
时间复杂度:O(3n)(n表示点数)
Code
{$inline on} var n,m,i,j,x,y,z,tot:longint; f:array[0..200000,0..17] of longint; pre,l,d:array[0..400000] of longint; dis,shen:array[0..200000] of longint; procedure insert(x,y:longint); inline; begin inc(tot); d[tot]:=y; pre[tot]:=l[x]; l[x]:=tot; end; procedure dg(now,k,q:longint); inline; var s:longint; begin shen[now]:=k; f[now,0]:=q; s:=l[now]; while s<>0 do begin if dis[d[s]]=0 then begin dis[d[s]]:=1; dg(d[s],k+1,now); end; s:=pre[s]; end; end; function yes(x,y:longint):longint; inline; var ans,k:longint; begin ans:=1; if shen[x]>shen[y] then begin while shen[x]>shen[y] do begin for k:=17 downto 0 do if shen[f[x,k]]>=shen[y] then break; x:=f[x,k]; ans:=ans+1 shl k; end; end; if shen[x]<shen[y] then begin while shen[x]<shen[y] do begin for k:=17 downto 0 do if shen[f[y,k]]>=shen[x] then break; y:=f[y,k]; ans:=ans+1 shl k; end; end; while x<>y do begin for k:=17 downto 0 do if (f[x,k]<>f[y,k]) and (f[x,k]<>0) and (f[y,k]<>0) then break; x:=f[x,k]; y:=f[y,k]; ans:=ans+1 shl (k+1); end; exit(ans); end; begin readln(n,m,x); for i:=1 to n-1 do begin readln(x,y); insert(x,y); insert(y,x); end; dis[1]:=1; shen[0]:=-maxlongint; dg(1,1,0); for j:=1 to 17 do for i:=1 to n do f[i,j]:=f[f[i,j-1],j-1]; while m>0 do begin readln(x,y,z); writeln((yes(x,y)+yes(y,z)-yes(x,z)+1) shr 1); dec(m); end; end.