爬楼梯

此博客链接：https://www.cnblogs.com/ping2yingshi/p/13716994.html

爬楼梯

题目链接：https://leetcode-cn.com/problems/climbing-stairs/

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

注意：给定 n 是一个正整数。

示例 1：

输入： 2
输出： 2
解释： 有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2：

输入： 3
输出： 3
解释： 有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

题解：

      思路：下面以8阶楼梯为例，效果图如下图所示。

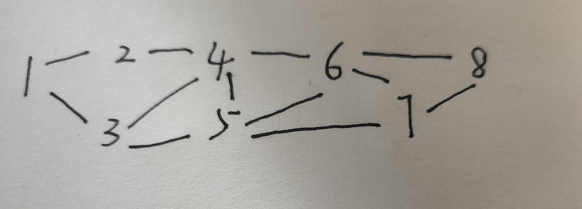
从图中可以看出，正向看时，每次到下一个台阶之前，可以有两种方案，可以走一步，也可以走两步，但是这要根据下一个台阶还够不够两个台阶，这样还需要判断，但是，如果你反向看，给知道了台阶数，到这个台阶之前，一定有两种方案到达当前台阶，那么我们可以逆向思维，每个台阶的数，都是由前面一个台阶的走法加上前面两个台阶的走法。所以n节台阶的走法总共有f(n)=f(n-1)+f(n-2)中走法。

代码：

class Solution {
    public int climbStairs(int n) {
        if(n==1)
           return 1;
        if(n==2)
        return 2;
       return climbStairs(n-1)+climbStairs(n-2);
    }
}

像上面这种代码，也是傻了，这好歹是力扣的题目，没有那么简单，当台阶到44时，就会超时。

 递归会超时的，改用循环。需要注意考虑台阶为1的情况，因为当台阶等于1时，定义的dp[2]数组会越界。

class Solution {
    public int climbStairs(int n) {

        int [] dp=new int [n+1];
        if(n==1)
        return 1;
       dp[1]=1;
       dp[2]=2;
       for(int i=3;i<=n;i++)
       dp[i]=dp[i-1]+dp[i-2];
       return dp[n];
    }
}

class Solution {
    public int climbStairs(int n) {

        int [] dp=new int [n+1];
        if(n==1)
        return 1;
       dp[1]=1;
       dp[2]=2;
       for(int i=3;i<=n;i++)
       dp[i]=dp[i-1]+dp[i-2];
       return dp[n];
    }
}